人教版物理选修3-1 3.6带电粒子在匀强磁场中的运动同步训练(含解析)
文档属性
| 名称 | 人教版物理选修3-1 3.6带电粒子在匀强磁场中的运动同步训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 593.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-04 14:01:41 | ||
图片预览




文档简介
人教版物理选修3-1
3.6带电粒子在匀强磁场中的运动同步训练
一、单项选择题(下列选项中只有一个选项满足题意)
1.两相邻匀强磁场区域的磁感应强度大小不同、方向平行.一速度方向与磁感应强度方向垂直的带电粒子(不计重力),从较弱磁场区域进入到较强磁场区域后,粒子的(
)
A.轨道半径减小,运动周期减小
B.轨道半径增大,运动周期增大
C.轨道半径减小,运动周期增大
D.轨道半径增大,运动周期减小
2.如图所示,回旋加速器D形盒的半径为R,用来加速质量为m,电量为q的质子,质子每次经过电场区时,都恰好在电压为U时并被加速,且电场可视为匀强电场,使质子由静止加速到能量为E后,由A孔射出.下列说法正确的是(
)
A.D形盒半径R、磁感应强度B不变,若加速电压U越高,质子的在加速器中的运动时间将不变.
B.D形盒半径R、磁感应强度B不变,若加速电压U越高,质子的在加速器中的运动时间将越长.
C.D形盒半径R、磁感应强度B不变,若加速电压U越高,质子飞出D形盒的动能EK将越大.
D.磁感应强度B不变,若加速电压U不变,
D形盒半径R越大、质子飞出D形盒的动能EK将越大
3.如图所示,一个电子沿AO方向垂直射入匀强磁场中,磁场只限于半径为R的圆内.若电子速度为v,质量为m,带电量为q,磁感应强度为B,电子在磁场中偏转后从C点射出,,下面结论正确的是( )
A.电子经过磁场的时间为
B.电子经过磁场的时间为
C.磁场半径R为
D.AC间的距离为
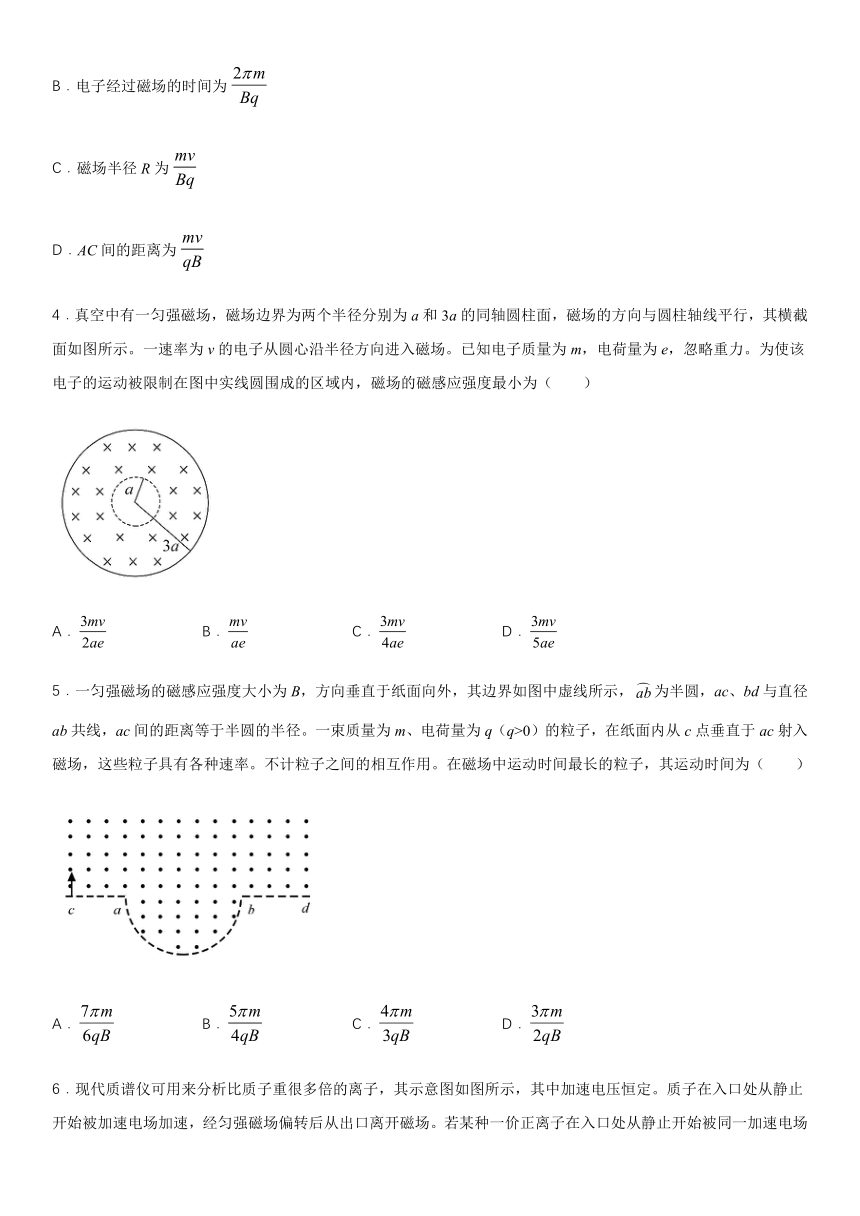
4.真空中有一匀强磁场,磁场边界为两个半径分别为a和3a的同轴圆柱面,磁场的方向与圆柱轴线平行,其横截面如图所示。一速率为v的电子从圆心沿半径方向进入磁场。已知电子质量为m,电荷量为e,忽略重力。为使该电子的运动被限制在图中实线圆围成的区域内,磁场的磁感应强度最小为( )
A.
B.
C.
D.
5.一匀强磁场的磁感应强度大小为B,方向垂直于纸面向外,其边界如图中虚线所示,为半圆,ac、bd与直径ab共线,ac间的距离等于半圆的半径。一束质量为m、电荷量为q(q>0)的粒子,在纸面内从c点垂直于ac射入磁场,这些粒子具有各种速率。不计粒子之间的相互作用。在磁场中运动时间最长的粒子,其运动时间为( )
A.
B.
C.
D.
6.现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压恒定。质子在入口处从静止开始被加速电场加速,经匀强磁场偏转后从出口离开磁场。若某种一价正离子在入口处从静止开始被同一加速电场加速,为使它经匀强磁场偏转后仍从同一出口离开磁场,需将磁感应强度增加到原来的12倍。此离子和质子的质量比约为
A.11
B.12
C.121
D.144
7.质量和电荷量都相等的带电粒子M和N,以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示。下列表述正确的是( )
A.M带负电,N带正电
B.M的速率小于N的速率
C.洛伦兹力对M、N做正功
D.M的运行时间大于N的运行时间
8.如图所示,有界匀强磁场边界线SP∥MN,速率不同的同种带电粒子(重力不计且忽略粒子间的相互作用)从S点沿SP方向同时射入磁场.其中穿过a点的粒子速度v1与MN垂直;穿过b点的粒子速度v2与MN成60°角,则粒子从S点分别到a、b所需时间之比为(
)
A.1∶3
B.4∶3
C.3∶2
D.1∶1
9.如图中是匀强磁场里的一片金属片,其平面与磁场方向平行,一个粒子从某点以与垂直的速度射出,动能是,该粒子在磁场中的运动轨迹如图所示。今测得它在金属片两边的轨道半径之比是,若在穿越金属板过程中粒子受到的阻力大小及电荷量恒定,则下列说法正确的是
A.该粒子的动能增加了
B.该粒子的动能减少了
C.该粒子做圆周运动的周期减小
D.该粒子最多能穿越金属板6次
10.如图所示,在屏MN的上方有磁感应强度为B的匀强磁场,磁场方向垂直纸面向里。P为屏上的一小孔,PC与MN垂直。一群质量为m、带电荷量为-q(q>0)的粒子(不计重力),以相同的速率v,从P处沿垂直于磁场的方向射入磁场区域。粒子入射方向在与磁场B垂直的平面内,且散开在与PC夹角为θ的范围内。则在屏MN上被粒子打中的区域的长度为( )
A.
B.
C.
D.
二、多项选择(下列各题中四个选项中有多个选项符合题意)
11.如图所示,空间中有垂直纸面向里的匀强磁场,垂直磁场方向的平面内有一长方形区域,其边长为L,边长为.两同种带电粒子(重力不计)以相同的速度分别从a点和ab边上的P点垂直射入磁场,速度方向垂直于ab边,两粒子都恰好经过c点,则下列说法中正确的是(
)
A.粒子在磁场中运动的轨道半径为
B.粒子从a点到c点的运动时间为
C.粒子的比荷为
D.P点与a点的距离为
12.如图所示,M.N为两块带等量异种电荷的平行金属板,两板间电压可取从零到某一最大值之间的各种数值.静止的带电粒子带电荷量为,质量为m(不计重力)从P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为,孔Q到板的下端C的距离为L,当M、N两板间电压取最大值时,粒子恰垂直打在CD板上,则(
)
A.两板间电压的最大值
B.CD板上可能被粒子打中区域的长度
C.粒子在磁场中运动的最长时间
D.能打到N板上的粒子的最大动能为
13.如图所示,在B=0.1T的匀强磁场(水平方向)中有一边长为L=8cm的正方形ABCD(竖直方向),内有一点P,它与AD和DC的距离均为1cm,在P点有一个发射正离子的装置,能够连续不断地向纸面内的各个方向发射出速率不同的正离子,离子的质量为1.0×10-14kg,电荷量为1.0×10-5C,离子的重力不计,不考虑离子之间的相互作用,则(
)
A.速率为5×106m/s的离子在磁场中运动的轨迹半径是5cm
B.速率在5×106m/s到8×105m/s范围内的离子不可能射出正方形区域
C.速率为5×106m/s的离子在CB边上可以射出磁场的范围为距C点距离
D.离子从CB边上射出正方形区域的最小速度为
14.如图所示,在纸面内半径为R的圆形区域中充满了垂直于纸面向里、磁感应强度为B的匀强磁场.一点电荷从图中A点以速度v0垂直磁场射入,速度方向与半径方向的夹角为30°.当该电荷离开磁场时,速度方向刚好改变了180°.不计电荷的重力,下列说法正确的是
A.该点电荷离开磁场时速度方向的反向延长线通过O点
B.该点电荷的比荷为
C.该点电荷在磁场中的运动时间为
D.该点电荷在磁场中的运动时间为
三、综合计算题(要求写出相应的计算过程)
15.如图所示,在xOy平面内有磁感应强度大小为B的匀强磁场,其中内磁场方向垂直xOy平面向里,在内磁场方向垂直xOy平面向外,在内无磁场.一个带正电的电荷量为q、质量为m的粒子(重力不计)在x轴上x=0处,以速度v0沿x轴正方向射入磁场.
(1)若v0未知,但粒子做圆周运动的轨迹半径为,求粒子与x轴的交点的x坐标.
(2)若无(1)中的条件限制,粒子的初速度仍为v0(已知),问粒子回到原点O需要使a为何值?
16.如图所示,在真空中,有一半径为r的圆形区域内充满垂直纸面向里的匀强磁场,磁感应强度为B,一带电粒子质量为m,电量为q,以某一速度由a点沿半径方向射入磁场,从c点射出磁场时其速度方向改变了60°,(粒子的重力可忽略)试求
(1)该粒子在磁场中的运动时间t;
(2)粒子做圆周运动的半径R;
(3)粒子运动的速度v。
17.提纯氘核技术对于核能利用具有重大价值.如是从质子、氘核混合物中将质子和氘核分离的原理图,x轴上方有垂直于纸面向外的匀强磁场,初速度为0的质子、氘核混合物经电压为U的电场加速后,从x轴上的A(﹣L,0)点沿与+x成θ=30°的方向进入第二象限(速度方向与磁场方向垂直),质子刚好从坐标原点离开磁场。已知质子、氘核的电荷量均为+q,质量分别为m、2m,忽略质子、氘核的重力及其相互作用。
(1)求质子进入磁场时速度的大小;
(2)求质子与氘核在磁场中运动的时间之比;
(3)若在x轴上接收氘核,求接收器所在位置的横坐标。
18.如图所示,在x轴上方存在匀强磁场,磁感应强度为B,方向垂直纸面向里.在x轴下方存在匀强电场,方向竖直向上.一个质量为m、电荷量为q、重力不计的带正电粒子从y轴上的a(0,h)点沿y轴正方向以某初速度开始运动,一段时间后,粒子与x轴正方向成45°进入电场,经过y轴的b点时速度方向恰好与y轴垂直.求:
(1)粒子在磁场中运动的轨道半径r和速度大小v1;
(2)匀强电场的电场强度大小E;
(3)粒子从开始到第三次经过x轴的时间t总.
参考答案
1.A
【解析】
根据洛伦兹力充当向心力可知,Bqv=,解得:
;故从较弱的磁场区域进入较强的磁场区域后粒子的轨道半径减小;由于洛伦兹力不做功,因此粒子运动的速度大小不变,由v=Rω可知,因半径减小,故角速度增大,周期减小,故A正确,BCD错误.故选A.
2.D
【解析】
ABC.在回旋加速器中,每经过电场一次,获得动能,根据洛仑兹力提供向心力:,当粒子半径等于回旋加速器半径时,粒子速度最大,动能最大:,与电压无关,所以
D形盒半径R、磁感应强度B不变,最大动能不变,但是每次获得动能增大,转的圈数减小,而每圈的时间是定值,所以加速时间将减小.ABC错误.
D.根据可知半径R越大、质子飞出D形盒的动能EK将越大,D正确.
3.D
【解析】
AB.由可得:
;
由图可知电子在磁场中转过的圆心角为60?,根据几何知识可知AC长等于半径:
,
,
电子转动的时间:
,
故A错误,B错误;
C.对AOC分析可知,半径
,
故C错误;
D.由于粒子的偏转角是60?,所以AC与粒子的偏转半径是相等的,为,故D正确;
4.C
【解析】
电子在磁场中做匀速圆周运动,由洛伦兹力提供向心力
则磁感应强度与圆周运动轨迹关系为
即运动轨迹半径越大,磁场的磁感应强度越小。令电子运动轨迹最大的半径为,为了使电子的运动被限制在图中实线圆围成的区域内,其最大半径的运动轨迹与实线圆相切,如图所示
A点为电子做圆周运动的圆心,电子从圆心沿半径方向进入磁场,由左手定则可得,,
为直角三角形,则由几何关系可得
解得
解得磁场的磁感应强度最小值
故选C。
5.C
【解析】
粒子在磁场中做匀速圆周运动
,
可得粒子在磁场中的周期
粒子在磁场中运动的时间
则粒子在磁场中运动的时间与速度无关,轨迹对应的圆心角越大,运动时间越长。采用放缩圆解决该问题,
粒子垂直ac射入磁场,则轨迹圆心必在ac直线上,将粒子的轨迹半径由零逐渐放大。
当半径和时,粒子分别从ac、bd区域射出,磁场中的轨迹为半圆,运动时间等于半个周期。
当0.5R粒子运动最长时间为
,
故选C。
6.D
【解析】
直线加速过程根据动能定理得
得
①
离子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律,有
得
②
①②两式联立得:
一价正离子电荷量与质子电荷量相等,同一加速电场U相同,同一出口离开磁场则R相同,所以m∝B2,磁感应强度增加到原来的12倍,离子质量是质子质量的144倍,D正确,A、B、C错误。
故选D。
7.A
【解析】
A.由左手定则判断出M带负电荷,N带正电荷,故A正确;
B.粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,则
得
在质量与电量相同的情况下,半径大说明其速率大,则知M的速度率大于N的速率,故B错误;
C.洛伦兹力方向与速度方向始终垂直,所以洛伦兹力对粒子不做功,故C错误;
D.粒子在磁场中运动半周,即时间为其周期的一半,而周期为,与粒子运动的速度无关,所以M的运行时间等于N的运行时间,故D错误。
故选A。
8.C
【解析】
粒子在磁场中运动的周期的公式为,由此可知,粒子的运动的时间与粒子的速度的大小无关,所以粒子在磁场中的周期相同;由粒子的运动的轨迹可知,通过a点的粒子的偏转角为90°,通过b点的粒子的偏转角为60°,所以通过a点的粒子的运动的时间为T/4,通过b点的粒子的运动的时间为T/6,所以从S到a.b所需时间t1:t2为3:2,所以C正确,ABD错误。
故选C。
9.B
【解析】
ABD.根据:
可得:
所以:
即:
又因为动能表达式:
所以开始的动能为:
穿过金属板后的动能:
粒子每穿过一次金属片损失的动能:
所以有:
即该粒子最多能穿过的金属板的次数为5次;故B正确,AD错误;
C.带电粒子在磁场中做圆周运动的周期,根据:
可得:
可知周期与速度无关,故C错误。
故选B。
10.A
【解析】
粒子做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得
解得
粒子沿着右侧边界射入,轨迹如图1
此时出射点最近,与边界交点与P间距为
粒子沿着左侧边界射入,轨迹如图2
此时出射点最近,与边界交点与P间距为
粒子垂直边界MN射入,轨迹如3图
此时出射点最远,与边界交点与P间距为2r,故范围为在荧光屏上P点右侧,将出现一条形亮线,其长度为
故A正确,BCD错误。
故选A。
11.ACD
【解析】
A、带电粒子在磁场中匀速圆周运动,画出运动轨迹图如图
从a点射入磁场的粒子,根据几何关系
,所以A正确;
B、从a点入射的粒子圆心在O?1,根据几何关系
∠bO?1c=60?,∠aO?1c=120?
从a到c运动时间,B错误;
C、由半径公式得:,C正确;
D、另一粒子由P点垂直入射,在△O?2bc中,O?2b=
Pb=,P与O1重合,所以P与a点的距离为,D正确.
故选ACD.
12.BCD
【解析】
粒子运动轨迹如图所示:
A、当M、N两板间电压取最大值时,粒子恰垂直打在CD板上,由几何知识得:,
粒子在磁场中做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得,
在加速电场中,由动能定理得:,解得:,故A错误;
B、设粒子轨迹与CD相切于H点,此时粒子半径为,粒子轨迹垂直打在CD边上的G点,则GH间距离即为粒子打中区域的长度s,根据几何关系:,解得:,根据几何关系可得粒子打中区域的长度:
,故B正确;
C、粒子在磁场中运动的周期为:粒子在磁场中运动的最大圆心角:,
所以粒子在磁场中运动的最长时间为:,故C错误;
D、当粒子在磁场的轨迹与CD边相切时,即粒子半径时,打到N板上的粒子的动能最大,最大动能:,根据洛伦兹力提供向心力可得:,解得:,故D正确.
本题是带电粒子在组合电场和磁场中运动的特殊情况:带电粒子先在电场中加速,后进入磁场做匀速圆周运动,由于加速电场的电压可变,导致进入磁场的速度变化、从而半径发生变化,要根据磁场区域的几何关系、根据选项的要求进入分析判断.
13.ACD
【解析】
A.离子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得,代入数据解得r1=0.05m=5cm,故A正确.
B.P点与AD和DC的距离均分1cm,轨迹半径的离子不可能射出正方形区域,由牛顿第二定律得,代入数据解得v=5×105m/s,速度v<5×105m/s的离子不能射出磁场区域,故B错误.
C.速度大小为v1=5×106m/s的离子的轨迹半径r1=5cm.当离子运动轨迹与CD边相切于E点时,离子将从BC边F点出射,为最低出射点.由几何关系得r12=(r1-d)2+PH2,解得PH=3cm,由几何关系得,F与C点的距离为;当离子运动轨迹与BC边相切于G点时,离子将从BC边G点出射,为最高出射点.由几何关系得r12=(L-r1-d)2+x2,解得,则出射点G距C点的距离.综上,出射点距C点的距离x满足.故C正确.
D.离子运动轨迹与CD相切又与BC相切是所有射出BC的轨迹中半径最小的,由几何知识可知,该轨迹半径,根据,得,故D正确.
14.BC
【解析】
试题分析:利用洛伦兹力提供向心力结合几何关系,联立即可求出粒子比荷,根据周期公式结合粒子在磁场中转过的圆心角,即可求出粒子在磁场中运动的时间;
由题意可画出粒子在磁场中的运动轨迹如图所示,A错误;由几何关系知粒子做圆周运动的半径为,结合,可得,B正确;粒子在磁场中的运动时间,C正确D错误.
15.(1)(2)
【解析】
(1)带电粒子在匀强磁场中做匀速圆周运动,其轨迹半径为R,其在第一象限的运动轨迹如图所示.此轨迹由两段圆弧组成,圆心分别在C和C'处,轨迹与x轴交点为P.由对称性可知,C'在x=2a直线上.设此直线与x轴交点为D,P点的x坐标为xP=2a+DP.过两段圆弧的连接点作平行于x轴的直线EF,则,,,,由此可得P点的x坐标为.
(2)若要求带电粒子能够返回原点,由对称性可知其运动轨迹如图所示,这时C'在x轴上.设∠CC'O=α,由几何关系得,.粒子入射速度为r0.
由牛顿第二定律和洛伦兹力提供向心力得,
解得.
16.(1);(2);(3)
【解析】
(1)设圆周运动半径为R,粒子做匀速圆周运动,洛伦兹力提供向心力
而
联立解得周期为
则粒子运动时间
(2)由几何关系有
(3)洛伦兹力提供向心力
解得
17.(1);(2)1:2;(3)(-1)L
【解析】
(1)质子在电场中加速,由动能定理得
qU=mv2﹣0
解得
(2)质子与氘核在磁场中都转过个圆周,
做圆周运动的周期
,
粒子在磁场中的运动时间
则
t1:t2=T1:T2=1:2
(3)质子在磁场中运动时,由几何知识得r=L
由牛顿第二定律得
氘核在电场中加速,由动能定理得
qU=2mv′2﹣0
在磁场中,由牛顿第二定律得
qv′B=2m
解得
R=L
横坐标
x=R﹣L=(﹣1)L
18.(1)(2)(3)
【解析】
(1)
根据题意可大体画出粒子在复合场中的运动轨迹如图所示,
由几何关系可得
rcos45°=h
即
解得
(2)
粒子第一次经过x轴的位置为x1,到达b点速度大小为vb
粒子做类平抛运动,有:
vb=v1cos45°
所以
设粒子进入电场经过时间t运动到b点,b点的纵坐标为-yb,
由类平抛运动得??
r+rsin45°=vbt
由动能定理
所以
(3)
粒子在磁场中的周期为
第一次经过x轴的时间
在电场中运动的时间
在第二次经过x轴到第三次经过x轴的时间
所以总时间
3.6带电粒子在匀强磁场中的运动同步训练
一、单项选择题(下列选项中只有一个选项满足题意)
1.两相邻匀强磁场区域的磁感应强度大小不同、方向平行.一速度方向与磁感应强度方向垂直的带电粒子(不计重力),从较弱磁场区域进入到较强磁场区域后,粒子的(
)
A.轨道半径减小,运动周期减小
B.轨道半径增大,运动周期增大
C.轨道半径减小,运动周期增大
D.轨道半径增大,运动周期减小
2.如图所示,回旋加速器D形盒的半径为R,用来加速质量为m,电量为q的质子,质子每次经过电场区时,都恰好在电压为U时并被加速,且电场可视为匀强电场,使质子由静止加速到能量为E后,由A孔射出.下列说法正确的是(
)
A.D形盒半径R、磁感应强度B不变,若加速电压U越高,质子的在加速器中的运动时间将不变.
B.D形盒半径R、磁感应强度B不变,若加速电压U越高,质子的在加速器中的运动时间将越长.
C.D形盒半径R、磁感应强度B不变,若加速电压U越高,质子飞出D形盒的动能EK将越大.
D.磁感应强度B不变,若加速电压U不变,
D形盒半径R越大、质子飞出D形盒的动能EK将越大
3.如图所示,一个电子沿AO方向垂直射入匀强磁场中,磁场只限于半径为R的圆内.若电子速度为v,质量为m,带电量为q,磁感应强度为B,电子在磁场中偏转后从C点射出,,下面结论正确的是( )
A.电子经过磁场的时间为
B.电子经过磁场的时间为
C.磁场半径R为
D.AC间的距离为
4.真空中有一匀强磁场,磁场边界为两个半径分别为a和3a的同轴圆柱面,磁场的方向与圆柱轴线平行,其横截面如图所示。一速率为v的电子从圆心沿半径方向进入磁场。已知电子质量为m,电荷量为e,忽略重力。为使该电子的运动被限制在图中实线圆围成的区域内,磁场的磁感应强度最小为( )
A.
B.
C.
D.
5.一匀强磁场的磁感应强度大小为B,方向垂直于纸面向外,其边界如图中虚线所示,为半圆,ac、bd与直径ab共线,ac间的距离等于半圆的半径。一束质量为m、电荷量为q(q>0)的粒子,在纸面内从c点垂直于ac射入磁场,这些粒子具有各种速率。不计粒子之间的相互作用。在磁场中运动时间最长的粒子,其运动时间为( )
A.
B.
C.
D.
6.现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压恒定。质子在入口处从静止开始被加速电场加速,经匀强磁场偏转后从出口离开磁场。若某种一价正离子在入口处从静止开始被同一加速电场加速,为使它经匀强磁场偏转后仍从同一出口离开磁场,需将磁感应强度增加到原来的12倍。此离子和质子的质量比约为
A.11
B.12
C.121
D.144
7.质量和电荷量都相等的带电粒子M和N,以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示。下列表述正确的是( )
A.M带负电,N带正电
B.M的速率小于N的速率
C.洛伦兹力对M、N做正功
D.M的运行时间大于N的运行时间
8.如图所示,有界匀强磁场边界线SP∥MN,速率不同的同种带电粒子(重力不计且忽略粒子间的相互作用)从S点沿SP方向同时射入磁场.其中穿过a点的粒子速度v1与MN垂直;穿过b点的粒子速度v2与MN成60°角,则粒子从S点分别到a、b所需时间之比为(
)
A.1∶3
B.4∶3
C.3∶2
D.1∶1
9.如图中是匀强磁场里的一片金属片,其平面与磁场方向平行,一个粒子从某点以与垂直的速度射出,动能是,该粒子在磁场中的运动轨迹如图所示。今测得它在金属片两边的轨道半径之比是,若在穿越金属板过程中粒子受到的阻力大小及电荷量恒定,则下列说法正确的是
A.该粒子的动能增加了
B.该粒子的动能减少了
C.该粒子做圆周运动的周期减小
D.该粒子最多能穿越金属板6次
10.如图所示,在屏MN的上方有磁感应强度为B的匀强磁场,磁场方向垂直纸面向里。P为屏上的一小孔,PC与MN垂直。一群质量为m、带电荷量为-q(q>0)的粒子(不计重力),以相同的速率v,从P处沿垂直于磁场的方向射入磁场区域。粒子入射方向在与磁场B垂直的平面内,且散开在与PC夹角为θ的范围内。则在屏MN上被粒子打中的区域的长度为( )
A.
B.
C.
D.
二、多项选择(下列各题中四个选项中有多个选项符合题意)
11.如图所示,空间中有垂直纸面向里的匀强磁场,垂直磁场方向的平面内有一长方形区域,其边长为L,边长为.两同种带电粒子(重力不计)以相同的速度分别从a点和ab边上的P点垂直射入磁场,速度方向垂直于ab边,两粒子都恰好经过c点,则下列说法中正确的是(
)
A.粒子在磁场中运动的轨道半径为
B.粒子从a点到c点的运动时间为
C.粒子的比荷为
D.P点与a点的距离为
12.如图所示,M.N为两块带等量异种电荷的平行金属板,两板间电压可取从零到某一最大值之间的各种数值.静止的带电粒子带电荷量为,质量为m(不计重力)从P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为,孔Q到板的下端C的距离为L,当M、N两板间电压取最大值时,粒子恰垂直打在CD板上,则(
)
A.两板间电压的最大值
B.CD板上可能被粒子打中区域的长度
C.粒子在磁场中运动的最长时间
D.能打到N板上的粒子的最大动能为
13.如图所示,在B=0.1T的匀强磁场(水平方向)中有一边长为L=8cm的正方形ABCD(竖直方向),内有一点P,它与AD和DC的距离均为1cm,在P点有一个发射正离子的装置,能够连续不断地向纸面内的各个方向发射出速率不同的正离子,离子的质量为1.0×10-14kg,电荷量为1.0×10-5C,离子的重力不计,不考虑离子之间的相互作用,则(
)
A.速率为5×106m/s的离子在磁场中运动的轨迹半径是5cm
B.速率在5×106m/s到8×105m/s范围内的离子不可能射出正方形区域
C.速率为5×106m/s的离子在CB边上可以射出磁场的范围为距C点距离
D.离子从CB边上射出正方形区域的最小速度为
14.如图所示,在纸面内半径为R的圆形区域中充满了垂直于纸面向里、磁感应强度为B的匀强磁场.一点电荷从图中A点以速度v0垂直磁场射入,速度方向与半径方向的夹角为30°.当该电荷离开磁场时,速度方向刚好改变了180°.不计电荷的重力,下列说法正确的是
A.该点电荷离开磁场时速度方向的反向延长线通过O点
B.该点电荷的比荷为
C.该点电荷在磁场中的运动时间为
D.该点电荷在磁场中的运动时间为
三、综合计算题(要求写出相应的计算过程)
15.如图所示,在xOy平面内有磁感应强度大小为B的匀强磁场,其中内磁场方向垂直xOy平面向里,在内磁场方向垂直xOy平面向外,在内无磁场.一个带正电的电荷量为q、质量为m的粒子(重力不计)在x轴上x=0处,以速度v0沿x轴正方向射入磁场.
(1)若v0未知,但粒子做圆周运动的轨迹半径为,求粒子与x轴的交点的x坐标.
(2)若无(1)中的条件限制,粒子的初速度仍为v0(已知),问粒子回到原点O需要使a为何值?
16.如图所示,在真空中,有一半径为r的圆形区域内充满垂直纸面向里的匀强磁场,磁感应强度为B,一带电粒子质量为m,电量为q,以某一速度由a点沿半径方向射入磁场,从c点射出磁场时其速度方向改变了60°,(粒子的重力可忽略)试求
(1)该粒子在磁场中的运动时间t;
(2)粒子做圆周运动的半径R;
(3)粒子运动的速度v。
17.提纯氘核技术对于核能利用具有重大价值.如是从质子、氘核混合物中将质子和氘核分离的原理图,x轴上方有垂直于纸面向外的匀强磁场,初速度为0的质子、氘核混合物经电压为U的电场加速后,从x轴上的A(﹣L,0)点沿与+x成θ=30°的方向进入第二象限(速度方向与磁场方向垂直),质子刚好从坐标原点离开磁场。已知质子、氘核的电荷量均为+q,质量分别为m、2m,忽略质子、氘核的重力及其相互作用。
(1)求质子进入磁场时速度的大小;
(2)求质子与氘核在磁场中运动的时间之比;
(3)若在x轴上接收氘核,求接收器所在位置的横坐标。
18.如图所示,在x轴上方存在匀强磁场,磁感应强度为B,方向垂直纸面向里.在x轴下方存在匀强电场,方向竖直向上.一个质量为m、电荷量为q、重力不计的带正电粒子从y轴上的a(0,h)点沿y轴正方向以某初速度开始运动,一段时间后,粒子与x轴正方向成45°进入电场,经过y轴的b点时速度方向恰好与y轴垂直.求:
(1)粒子在磁场中运动的轨道半径r和速度大小v1;
(2)匀强电场的电场强度大小E;
(3)粒子从开始到第三次经过x轴的时间t总.
参考答案
1.A
【解析】
根据洛伦兹力充当向心力可知,Bqv=,解得:
;故从较弱的磁场区域进入较强的磁场区域后粒子的轨道半径减小;由于洛伦兹力不做功,因此粒子运动的速度大小不变,由v=Rω可知,因半径减小,故角速度增大,周期减小,故A正确,BCD错误.故选A.
2.D
【解析】
ABC.在回旋加速器中,每经过电场一次,获得动能,根据洛仑兹力提供向心力:,当粒子半径等于回旋加速器半径时,粒子速度最大,动能最大:,与电压无关,所以
D形盒半径R、磁感应强度B不变,最大动能不变,但是每次获得动能增大,转的圈数减小,而每圈的时间是定值,所以加速时间将减小.ABC错误.
D.根据可知半径R越大、质子飞出D形盒的动能EK将越大,D正确.
3.D
【解析】
AB.由可得:
;
由图可知电子在磁场中转过的圆心角为60?,根据几何知识可知AC长等于半径:
,
,
电子转动的时间:
,
故A错误,B错误;
C.对AOC分析可知,半径
,
故C错误;
D.由于粒子的偏转角是60?,所以AC与粒子的偏转半径是相等的,为,故D正确;
4.C
【解析】
电子在磁场中做匀速圆周运动,由洛伦兹力提供向心力
则磁感应强度与圆周运动轨迹关系为
即运动轨迹半径越大,磁场的磁感应强度越小。令电子运动轨迹最大的半径为,为了使电子的运动被限制在图中实线圆围成的区域内,其最大半径的运动轨迹与实线圆相切,如图所示
A点为电子做圆周运动的圆心,电子从圆心沿半径方向进入磁场,由左手定则可得,,
为直角三角形,则由几何关系可得
解得
解得磁场的磁感应强度最小值
故选C。
5.C
【解析】
粒子在磁场中做匀速圆周运动
,
可得粒子在磁场中的周期
粒子在磁场中运动的时间
则粒子在磁场中运动的时间与速度无关,轨迹对应的圆心角越大,运动时间越长。采用放缩圆解决该问题,
粒子垂直ac射入磁场,则轨迹圆心必在ac直线上,将粒子的轨迹半径由零逐渐放大。
当半径和时,粒子分别从ac、bd区域射出,磁场中的轨迹为半圆,运动时间等于半个周期。
当0.5R
,
故选C。
6.D
【解析】
直线加速过程根据动能定理得
得
①
离子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律,有
得
②
①②两式联立得:
一价正离子电荷量与质子电荷量相等,同一加速电场U相同,同一出口离开磁场则R相同,所以m∝B2,磁感应强度增加到原来的12倍,离子质量是质子质量的144倍,D正确,A、B、C错误。
故选D。
7.A
【解析】
A.由左手定则判断出M带负电荷,N带正电荷,故A正确;
B.粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,则
得
在质量与电量相同的情况下,半径大说明其速率大,则知M的速度率大于N的速率,故B错误;
C.洛伦兹力方向与速度方向始终垂直,所以洛伦兹力对粒子不做功,故C错误;
D.粒子在磁场中运动半周,即时间为其周期的一半,而周期为,与粒子运动的速度无关,所以M的运行时间等于N的运行时间,故D错误。
故选A。
8.C
【解析】
粒子在磁场中运动的周期的公式为,由此可知,粒子的运动的时间与粒子的速度的大小无关,所以粒子在磁场中的周期相同;由粒子的运动的轨迹可知,通过a点的粒子的偏转角为90°,通过b点的粒子的偏转角为60°,所以通过a点的粒子的运动的时间为T/4,通过b点的粒子的运动的时间为T/6,所以从S到a.b所需时间t1:t2为3:2,所以C正确,ABD错误。
故选C。
9.B
【解析】
ABD.根据:
可得:
所以:
即:
又因为动能表达式:
所以开始的动能为:
穿过金属板后的动能:
粒子每穿过一次金属片损失的动能:
所以有:
即该粒子最多能穿过的金属板的次数为5次;故B正确,AD错误;
C.带电粒子在磁场中做圆周运动的周期,根据:
可得:
可知周期与速度无关,故C错误。
故选B。
10.A
【解析】
粒子做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得
解得
粒子沿着右侧边界射入,轨迹如图1
此时出射点最近,与边界交点与P间距为
粒子沿着左侧边界射入,轨迹如图2
此时出射点最近,与边界交点与P间距为
粒子垂直边界MN射入,轨迹如3图
此时出射点最远,与边界交点与P间距为2r,故范围为在荧光屏上P点右侧,将出现一条形亮线,其长度为
故A正确,BCD错误。
故选A。
11.ACD
【解析】
A、带电粒子在磁场中匀速圆周运动,画出运动轨迹图如图
从a点射入磁场的粒子,根据几何关系
,所以A正确;
B、从a点入射的粒子圆心在O?1,根据几何关系
∠bO?1c=60?,∠aO?1c=120?
从a到c运动时间,B错误;
C、由半径公式得:,C正确;
D、另一粒子由P点垂直入射,在△O?2bc中,O?2b=
Pb=,P与O1重合,所以P与a点的距离为,D正确.
故选ACD.
12.BCD
【解析】
粒子运动轨迹如图所示:
A、当M、N两板间电压取最大值时,粒子恰垂直打在CD板上,由几何知识得:,
粒子在磁场中做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得,
在加速电场中,由动能定理得:,解得:,故A错误;
B、设粒子轨迹与CD相切于H点,此时粒子半径为,粒子轨迹垂直打在CD边上的G点,则GH间距离即为粒子打中区域的长度s,根据几何关系:,解得:,根据几何关系可得粒子打中区域的长度:
,故B正确;
C、粒子在磁场中运动的周期为:粒子在磁场中运动的最大圆心角:,
所以粒子在磁场中运动的最长时间为:,故C错误;
D、当粒子在磁场的轨迹与CD边相切时,即粒子半径时,打到N板上的粒子的动能最大,最大动能:,根据洛伦兹力提供向心力可得:,解得:,故D正确.
本题是带电粒子在组合电场和磁场中运动的特殊情况:带电粒子先在电场中加速,后进入磁场做匀速圆周运动,由于加速电场的电压可变,导致进入磁场的速度变化、从而半径发生变化,要根据磁场区域的几何关系、根据选项的要求进入分析判断.
13.ACD
【解析】
A.离子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得,代入数据解得r1=0.05m=5cm,故A正确.
B.P点与AD和DC的距离均分1cm,轨迹半径的离子不可能射出正方形区域,由牛顿第二定律得,代入数据解得v=5×105m/s,速度v<5×105m/s的离子不能射出磁场区域,故B错误.
C.速度大小为v1=5×106m/s的离子的轨迹半径r1=5cm.当离子运动轨迹与CD边相切于E点时,离子将从BC边F点出射,为最低出射点.由几何关系得r12=(r1-d)2+PH2,解得PH=3cm,由几何关系得,F与C点的距离为;当离子运动轨迹与BC边相切于G点时,离子将从BC边G点出射,为最高出射点.由几何关系得r12=(L-r1-d)2+x2,解得,则出射点G距C点的距离.综上,出射点距C点的距离x满足.故C正确.
D.离子运动轨迹与CD相切又与BC相切是所有射出BC的轨迹中半径最小的,由几何知识可知,该轨迹半径,根据,得,故D正确.
14.BC
【解析】
试题分析:利用洛伦兹力提供向心力结合几何关系,联立即可求出粒子比荷,根据周期公式结合粒子在磁场中转过的圆心角,即可求出粒子在磁场中运动的时间;
由题意可画出粒子在磁场中的运动轨迹如图所示,A错误;由几何关系知粒子做圆周运动的半径为,结合,可得,B正确;粒子在磁场中的运动时间,C正确D错误.
15.(1)(2)
【解析】
(1)带电粒子在匀强磁场中做匀速圆周运动,其轨迹半径为R,其在第一象限的运动轨迹如图所示.此轨迹由两段圆弧组成,圆心分别在C和C'处,轨迹与x轴交点为P.由对称性可知,C'在x=2a直线上.设此直线与x轴交点为D,P点的x坐标为xP=2a+DP.过两段圆弧的连接点作平行于x轴的直线EF,则,,,,由此可得P点的x坐标为.
(2)若要求带电粒子能够返回原点,由对称性可知其运动轨迹如图所示,这时C'在x轴上.设∠CC'O=α,由几何关系得,.粒子入射速度为r0.
由牛顿第二定律和洛伦兹力提供向心力得,
解得.
16.(1);(2);(3)
【解析】
(1)设圆周运动半径为R,粒子做匀速圆周运动,洛伦兹力提供向心力
而
联立解得周期为
则粒子运动时间
(2)由几何关系有
(3)洛伦兹力提供向心力
解得
17.(1);(2)1:2;(3)(-1)L
【解析】
(1)质子在电场中加速,由动能定理得
qU=mv2﹣0
解得
(2)质子与氘核在磁场中都转过个圆周,
做圆周运动的周期
,
粒子在磁场中的运动时间
则
t1:t2=T1:T2=1:2
(3)质子在磁场中运动时,由几何知识得r=L
由牛顿第二定律得
氘核在电场中加速,由动能定理得
qU=2mv′2﹣0
在磁场中,由牛顿第二定律得
qv′B=2m
解得
R=L
横坐标
x=R﹣L=(﹣1)L
18.(1)(2)(3)
【解析】
(1)
根据题意可大体画出粒子在复合场中的运动轨迹如图所示,
由几何关系可得
rcos45°=h
即
解得
(2)
粒子第一次经过x轴的位置为x1,到达b点速度大小为vb
粒子做类平抛运动,有:
vb=v1cos45°
所以
设粒子进入电场经过时间t运动到b点,b点的纵坐标为-yb,
由类平抛运动得??
r+rsin45°=vbt
由动能定理
所以
(3)
粒子在磁场中的周期为
第一次经过x轴的时间
在电场中运动的时间
在第二次经过x轴到第三次经过x轴的时间
所以总时间
