相似三角形
图片预览

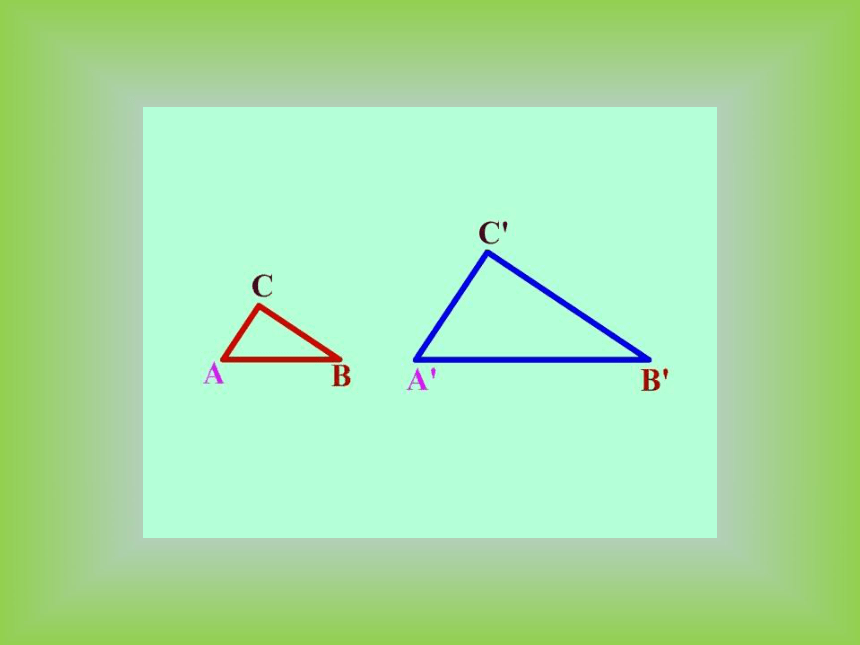
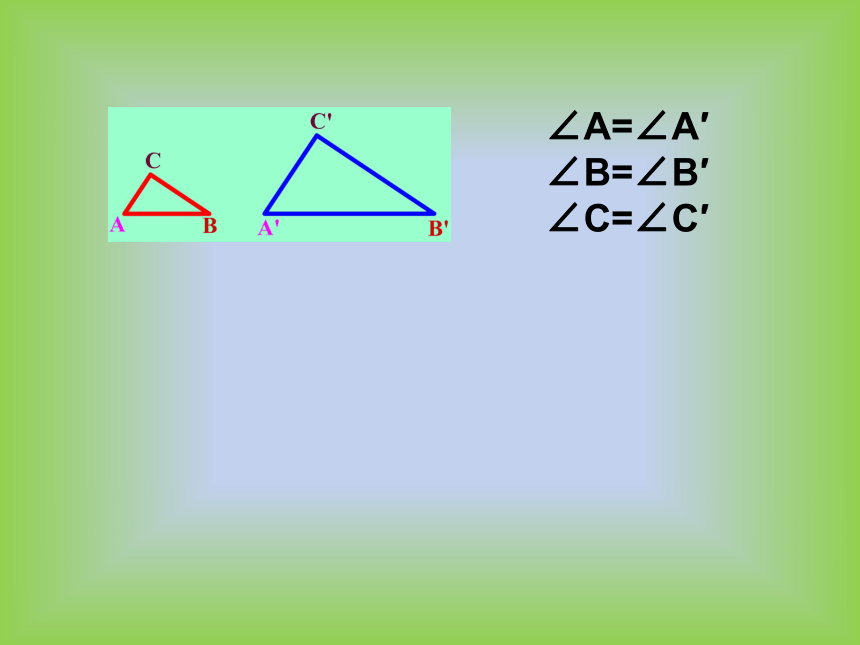
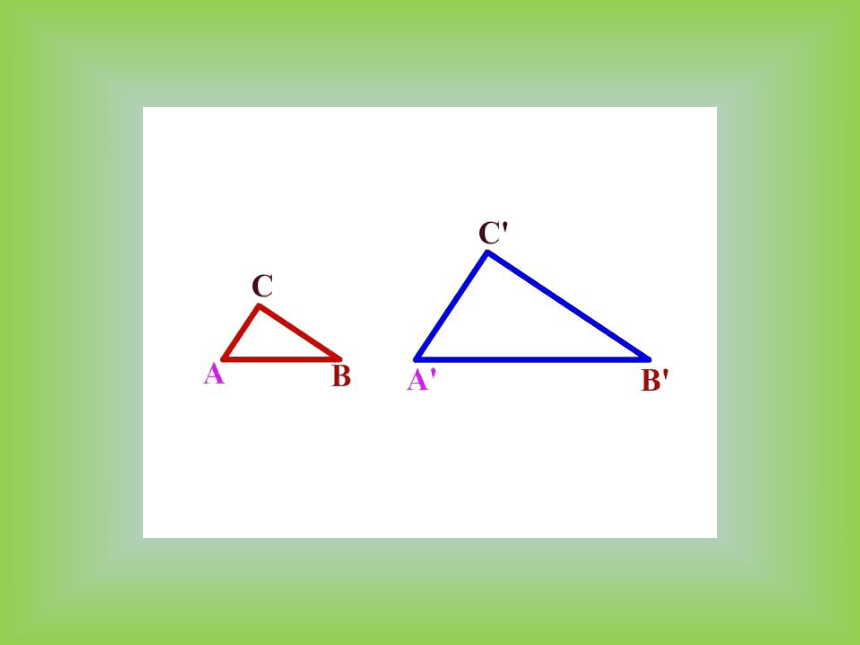

文档简介
(共21张PPT)
蓬莱市郝斌中学 赵慧超
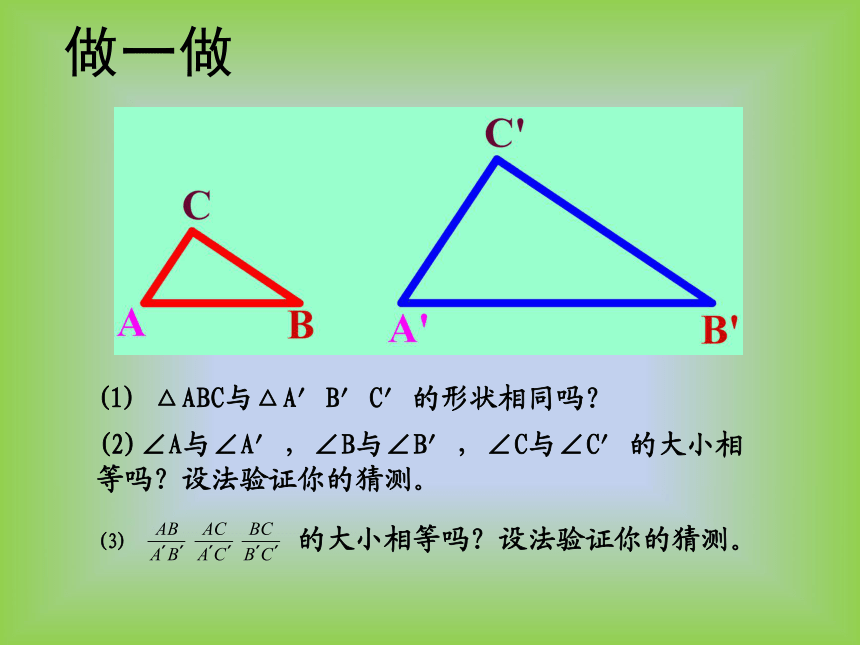
做一做
(1) △ABC与△A′B′C′的形状相同吗?
的大小相等吗?设法验证你的猜测。
(2)∠A与∠A′,∠B与∠B′,∠C与∠C′的大小相等吗?设法验证你的猜测。
(3)
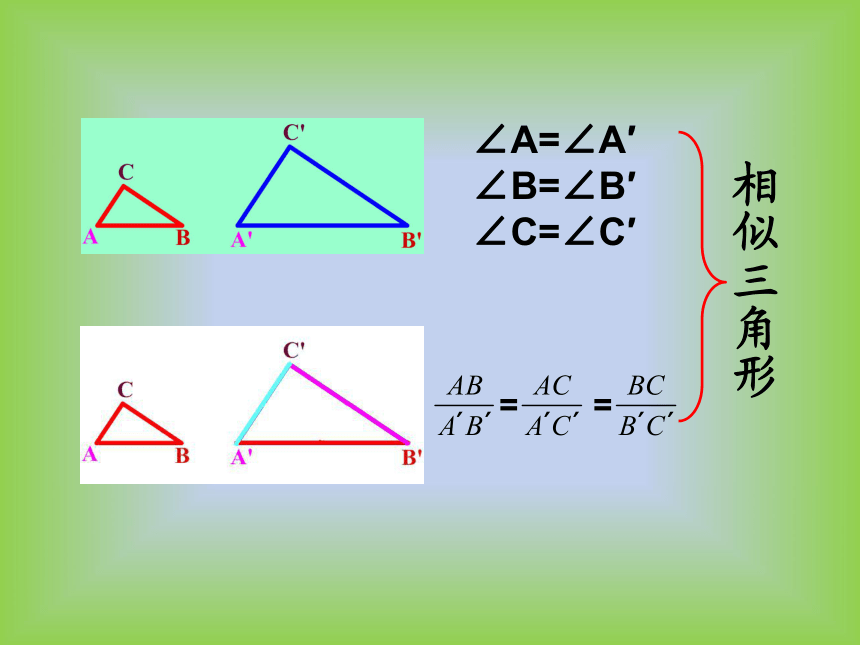
∠A=∠A′
∠B=∠B′
∠C=∠C′
∠A=∠A′
∠B=∠B′
∠C=∠C′
=
=
相似三角形
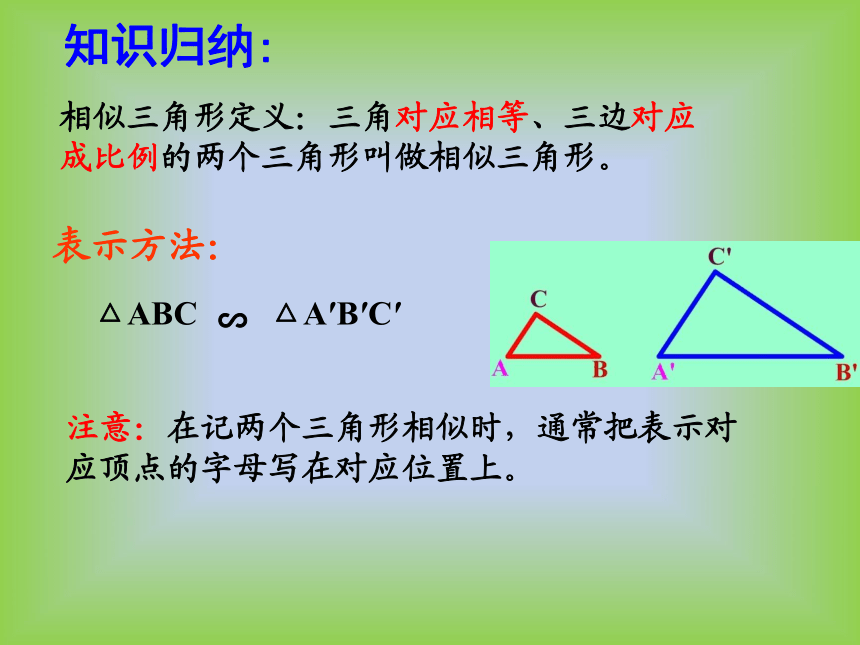
知识归纳:
相似三角形定义:三角对应相等、三边对应成比例的两个三角形叫做相似三角形。
表示方法:
注意:在记两个三角形相似时,通常把表示对应顶点的字母写在对应位置上。
△ABC
∽
△A′B′C′
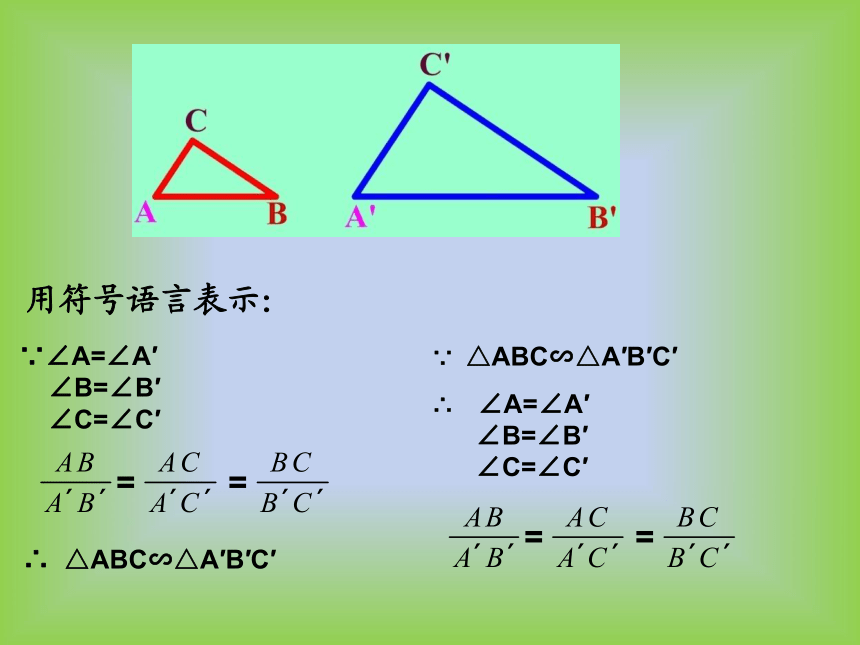
用符号语言表示:
∵∠A=∠A′
∠B=∠B′
∠C=∠C′
∴ △ABC∽△A′B′C′
=
=
=
=
∵ △ABC∽△A′B′C′
∴ ∠A=∠A′
∠B=∠B′
∠C=∠C′
判断下列各对三角形是否相似。正确的打√错误的打×,并说明理由。
(1)两个全等三角形一定相似。 ( )
(2)两个等腰直角三角形一定相似。( )
(3)两个直角三角形一定相似。 ( )
(4)两个等边三角形一定相似。 ( )
(5)两个等腰三角形一定相似。 ( )
议一议:
√
×
√
√
×
1、已知△ABC∽△DEF ,哪些角是对应角?哪些边是对应边?
想一想:
对应角有什么关系?对应边呢?
相似比:相似三角形对应边的比叫做相似比(用字母k表示)。
注意:三角形的相似比有顺序性,△ABC与△DEF的相似比为k1,△DEF与△ABC的相似比为k2,则k1= 。两个全等三角形的相似比是1。
知识归纳:
实践应用
例1 如图有一块三角形的草坪,其中一边的长是20米,在这个草坪的图纸上,这条边的长画成5厘米,其他两边长都画成3.5厘米,求该草坪其他两边的实际长度。
20m
5cm
3.5cm
3.5cm
xcm
xcm
解:设其他两边的实际长度都是x厘米。
由题知两个三角形相似,且相似比是2000:5=400:1
∴
=
∴ x=1400(厘米)=14米
答:该草坪其他两边的实际长度都是14米。
拓展提高
例2 如图,已知△ADE∽△ABC
( 1)如果∠BAC=45°,∠ACB=40°,
求∠AED和∠ADE的度数
(2)如果AE=50cm,EC=30cm,BC=70cm,求DE的长
变式练习
如图:△ADE∽△ABC,如果AD:BD=1:3,BC=70cm,求DE的长。
1、相似三角形的定义:对应角相等、对应边成比例的两个三角形。
2、表示方法:
3、相似比: 相似三角形对应边的比(有顺序性)。
4、相似三角形的性质:对应角相等、对应边成比例。
5、 利用相似三角形的性质求角和边。
△ABC
△A′B′C′
∽
本节课的收获:
分层检测:
1、已知△ABC∽△DEF,AB=3cm,
BC=4cm,CA=2cm,
EF=6cm,那么DE= ( ) DF= ( )
2、已知两个三角形相似,其中一个三角形的两个内角
分别为 50°和 60°, 则另一个三角形的最大内
角为( ) 。最小内角为( ) 。
拓展:已知Rt△ABC的两条直角边的长分别为5和12,Rt△ABC∽Rt△A′B′C′,且Rt△A′B′C′的最长边为52,则Rt△A′B′C′的周长为( ) 。
A
B
C
A’
B’
C’
a
a
b
b
2、已知△ABC∽△DEF ,AC=2cm,DF =3cm
△ABC与△DEF的相似比k1=
△DEF与△ABC的相似比k2=
K1和k2有什么关系?当这两个相似比相等时,两个三角形之间有什么关系?
想一想:
想一想:
3、已知△ABC∽△DEF ,AC=2cm,DF =3cm
若BC=4cm,你能求出哪条线段?
即
=
∴EF =
= 6
解:∵ △ABC∽△DEF
∴
=
课后延伸
必做:课本35页 随堂练习1、2
选作:课本35页 随堂练习3
蓬莱市郝斌中学 赵慧超
做一做
(1) △ABC与△A′B′C′的形状相同吗?
的大小相等吗?设法验证你的猜测。
(2)∠A与∠A′,∠B与∠B′,∠C与∠C′的大小相等吗?设法验证你的猜测。
(3)
∠A=∠A′
∠B=∠B′
∠C=∠C′
∠A=∠A′
∠B=∠B′
∠C=∠C′
=
=
相似三角形
知识归纳:
相似三角形定义:三角对应相等、三边对应成比例的两个三角形叫做相似三角形。
表示方法:
注意:在记两个三角形相似时,通常把表示对应顶点的字母写在对应位置上。
△ABC
∽
△A′B′C′
用符号语言表示:
∵∠A=∠A′
∠B=∠B′
∠C=∠C′
∴ △ABC∽△A′B′C′
=
=
=
=
∵ △ABC∽△A′B′C′
∴ ∠A=∠A′
∠B=∠B′
∠C=∠C′
判断下列各对三角形是否相似。正确的打√错误的打×,并说明理由。
(1)两个全等三角形一定相似。 ( )
(2)两个等腰直角三角形一定相似。( )
(3)两个直角三角形一定相似。 ( )
(4)两个等边三角形一定相似。 ( )
(5)两个等腰三角形一定相似。 ( )
议一议:
√
×
√
√
×
1、已知△ABC∽△DEF ,哪些角是对应角?哪些边是对应边?
想一想:
对应角有什么关系?对应边呢?
相似比:相似三角形对应边的比叫做相似比(用字母k表示)。
注意:三角形的相似比有顺序性,△ABC与△DEF的相似比为k1,△DEF与△ABC的相似比为k2,则k1= 。两个全等三角形的相似比是1。
知识归纳:
实践应用
例1 如图有一块三角形的草坪,其中一边的长是20米,在这个草坪的图纸上,这条边的长画成5厘米,其他两边长都画成3.5厘米,求该草坪其他两边的实际长度。
20m
5cm
3.5cm
3.5cm
xcm
xcm
解:设其他两边的实际长度都是x厘米。
由题知两个三角形相似,且相似比是2000:5=400:1
∴
=
∴ x=1400(厘米)=14米
答:该草坪其他两边的实际长度都是14米。
拓展提高
例2 如图,已知△ADE∽△ABC
( 1)如果∠BAC=45°,∠ACB=40°,
求∠AED和∠ADE的度数
(2)如果AE=50cm,EC=30cm,BC=70cm,求DE的长
变式练习
如图:△ADE∽△ABC,如果AD:BD=1:3,BC=70cm,求DE的长。
1、相似三角形的定义:对应角相等、对应边成比例的两个三角形。
2、表示方法:
3、相似比: 相似三角形对应边的比(有顺序性)。
4、相似三角形的性质:对应角相等、对应边成比例。
5、 利用相似三角形的性质求角和边。
△ABC
△A′B′C′
∽
本节课的收获:
分层检测:
1、已知△ABC∽△DEF,AB=3cm,
BC=4cm,CA=2cm,
EF=6cm,那么DE= ( ) DF= ( )
2、已知两个三角形相似,其中一个三角形的两个内角
分别为 50°和 60°, 则另一个三角形的最大内
角为( ) 。最小内角为( ) 。
拓展:已知Rt△ABC的两条直角边的长分别为5和12,Rt△ABC∽Rt△A′B′C′,且Rt△A′B′C′的最长边为52,则Rt△A′B′C′的周长为( ) 。
A
B
C
A’
B’
C’
a
a
b
b
2、已知△ABC∽△DEF ,AC=2cm,DF =3cm
△ABC与△DEF的相似比k1=
△DEF与△ABC的相似比k2=
K1和k2有什么关系?当这两个相似比相等时,两个三角形之间有什么关系?
想一想:
想一想:
3、已知△ABC∽△DEF ,AC=2cm,DF =3cm
若BC=4cm,你能求出哪条线段?
即
=
∴EF =
= 6
解:∵ △ABC∽△DEF
∴
=
课后延伸
必做:课本35页 随堂练习1、2
选作:课本35页 随堂练习3
