14.1.1直角三角形的三边关系学案
文档属性
| 名称 | 14.1.1直角三角形的三边关系学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 66.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-17 00:00:00 | ||
图片预览

文档简介
14.1 直角三角形的三边关系~~学案
学习目标:1、学生通过预习、合作、交流初步探索直角三角形的三边关系。
2、能利用直角三角形的三边关系解决直角三角形的边长和面积的计算问题。
学习重点:探索直角三角形的三边关系(勾股定理)及数形结合思想。
学习难点:熟练运用直角三角形的三边关系解决有关的计算问题及分类讨论和方程思想。
① (c为斜边)
公式
公式变形
一、预习:
1、结合教材,通过自主学习、合作学习初步探索出直角三角形的三边具有怎样的特殊关系?
2、利用直角三角形的三边关系可以解决哪些问题?(请列举或举例说明)
二、反馈
1、Rt⊿ABC中,∠C=90°,(1)若a=5, b=12, 则c= ;
(2)若a=7, c=25, 则b= ;
(3)若a∶b=3∶4, c=10 则a= .
2、已知矩形的邻边之比为4∶3,且周长为42cm,则矩形的对角线长为 cm。
3、已知Rt⊿ABC中,∠A=90°,a=25cm, b=24cm, 求第三边c .
三、解疑
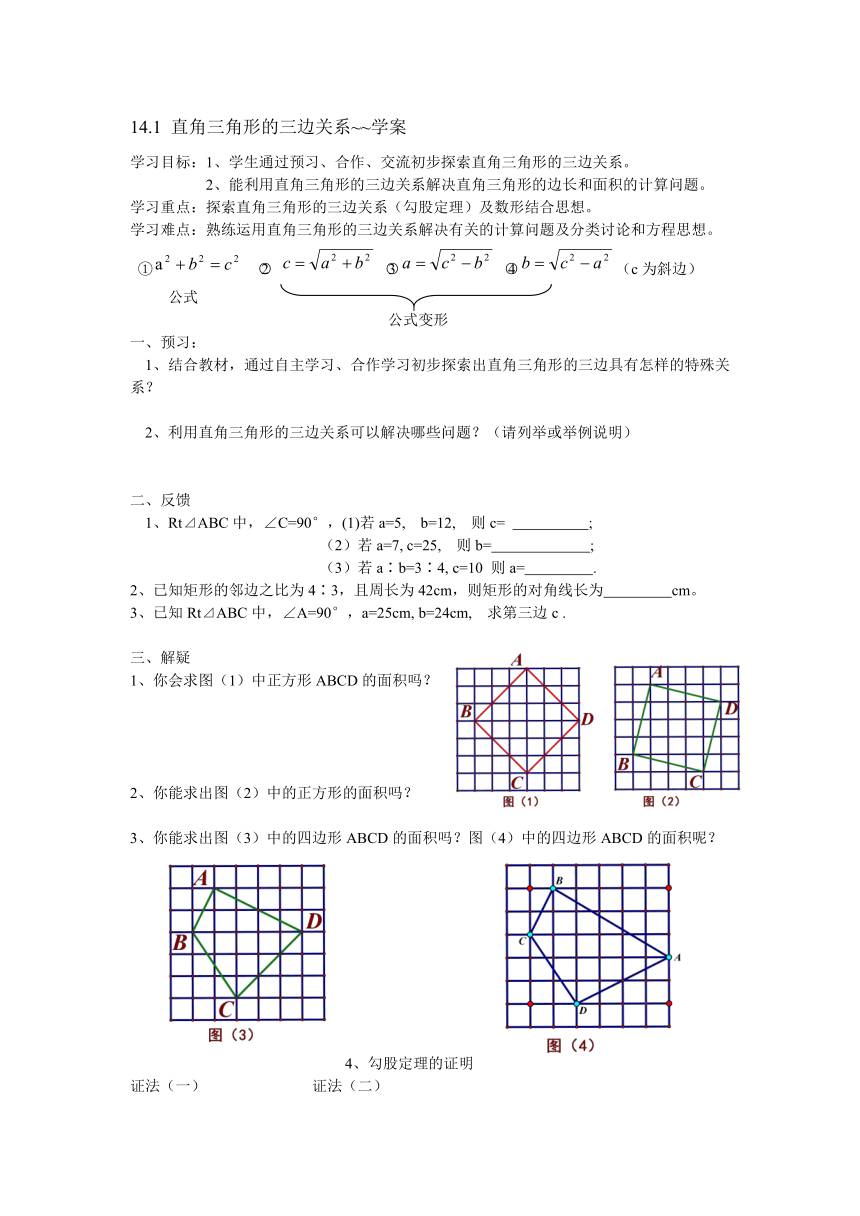
1、你会求图(1)中正方形ABCD的面积吗?
2、你能求出图(2)中的正方形的面积吗?
3、你能求出图(3)中的四边形ABCD的面积吗?图(4)中的四边形ABCD的面积呢?
4、勾股定理的证明
证法(一) 证法(二)
四、练习
1、在Rt⊿ABC中,∠C=90°,下列式子成立的是( )
A、AB2+BC2=AC2 B、AB2-BC2=AC2
C、BC2=AB2+AC2 D、BC2-AB2=AC2
2、已知一直角三角形的两条边长分别为3cm和4cm ,则第三边的长是 cm.(保留根号)
3、如图,一架17m长的云梯斜靠在MC墙面上,梯子的顶端A距墙根15m,求梯子的底端B距墙根的距离。(注意解题格式)
五、反馈
1、如图,S1=169cm2,
S2=144cm2,则
S3= cm2.
2、在Rt⊿ABC中,
∠C=90°斜边AB=2cm,则AB2+BC2+CA2= cm2
3、一根长为4cm的铅芯放置在底面直径为1cm,高为3cm的无盖圆筒中,铅芯露出圆筒的长度为xcm,则x的取值范围是 。
4、如图,是由16块边长为1m的正方形地砖铺设的地面示意 图,小明沿图中所示的折线从A经 B 到 C所走的
路程为 m.(结果保留根号)
5、已知Rt⊿ABC中,∠C=90°,BC=8cm, AB=17cm,
求该三角形的斜边上的高CD的长及面积。
学习目标:1、学生通过预习、合作、交流初步探索直角三角形的三边关系。
2、能利用直角三角形的三边关系解决直角三角形的边长和面积的计算问题。
学习重点:探索直角三角形的三边关系(勾股定理)及数形结合思想。
学习难点:熟练运用直角三角形的三边关系解决有关的计算问题及分类讨论和方程思想。
① (c为斜边)
公式
公式变形
一、预习:
1、结合教材,通过自主学习、合作学习初步探索出直角三角形的三边具有怎样的特殊关系?
2、利用直角三角形的三边关系可以解决哪些问题?(请列举或举例说明)
二、反馈
1、Rt⊿ABC中,∠C=90°,(1)若a=5, b=12, 则c= ;
(2)若a=7, c=25, 则b= ;
(3)若a∶b=3∶4, c=10 则a= .
2、已知矩形的邻边之比为4∶3,且周长为42cm,则矩形的对角线长为 cm。
3、已知Rt⊿ABC中,∠A=90°,a=25cm, b=24cm, 求第三边c .
三、解疑
1、你会求图(1)中正方形ABCD的面积吗?
2、你能求出图(2)中的正方形的面积吗?
3、你能求出图(3)中的四边形ABCD的面积吗?图(4)中的四边形ABCD的面积呢?
4、勾股定理的证明
证法(一) 证法(二)
四、练习
1、在Rt⊿ABC中,∠C=90°,下列式子成立的是( )
A、AB2+BC2=AC2 B、AB2-BC2=AC2
C、BC2=AB2+AC2 D、BC2-AB2=AC2
2、已知一直角三角形的两条边长分别为3cm和4cm ,则第三边的长是 cm.(保留根号)
3、如图,一架17m长的云梯斜靠在MC墙面上,梯子的顶端A距墙根15m,求梯子的底端B距墙根的距离。(注意解题格式)
五、反馈
1、如图,S1=169cm2,
S2=144cm2,则
S3= cm2.
2、在Rt⊿ABC中,
∠C=90°斜边AB=2cm,则AB2+BC2+CA2= cm2
3、一根长为4cm的铅芯放置在底面直径为1cm,高为3cm的无盖圆筒中,铅芯露出圆筒的长度为xcm,则x的取值范围是 。
4、如图,是由16块边长为1m的正方形地砖铺设的地面示意 图,小明沿图中所示的折线从A经 B 到 C所走的
路程为 m.(结果保留根号)
5、已知Rt⊿ABC中,∠C=90°,BC=8cm, AB=17cm,
求该三角形的斜边上的高CD的长及面积。
