2020年秋苏科版九年级数学上册 第4章 等可能条件下的概率单元测试卷(含解析)
文档属性
| 名称 | 2020年秋苏科版九年级数学上册 第4章 等可能条件下的概率单元测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 21:17:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020年秋苏科版九年级数学上册第4章 等可能条件下的概率单元测试卷解析版
一、选择题
1.投掷一枚普通的正方体骰子,有下列事件:①掷得的点数是6;②掷得的点数是奇数;③掷得的点数不大于4;④掷得的点数不小于2,这些事件发生的可能性由大到小排列正确的是(?? ).
A.?①②③④???????????????????????????B.?④③②①???????????????????????????C.?③④②①???????????????????????????D.?②③①④
2.一个质地均匀的小正方体的六个面上分别标有数字1,2,3,4,5,6.如果任意抛掷小正方体两次,那么下列说法正确的是(?? ).
A.?得到的数字和必然是4?????????????????????????????????????????B.?得到的数字和可能是3
C.?得到的数字和不可能是2?????????????????????????????????????D.?得到的数字和有可能是1
3.已知电流在一定时间段内正常通过电子元件“ ”的概率是0.5;则在一定时间段内,由该元件组成的图示电路A、B之间,电流能够正常通过的概率是(??? )
A.?0.75?????????????????????????????????????B.?0.625?????????????????????????????????????C.?0.5?????????????????????????????????????D.?0.25
4.已知一个质地均匀的正四面体的每个面上分别标有1,2,3,4四个数字,抛掷这个正四面体,则接地的那一面为偶数的概率为(??? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
5.如图,飞镖游戏板中每一块小正方形除颜色外都相同。若一个人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是(??? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
6.一个不透明的袋子中有3个白球、2个黄球和1个红球,这些球除颜色外其他完全相同,那么从袋子中随机摸出一个球是黄球的概率为( ???)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
7.一个密码箱的密码,每个位数上的数都是从0到9的自然数,若要使不知道密码的一次就拨对密码的概率小于 ,则密码的位数至少需要(???? )位.
A.?3位??????????????????????????????????????B.?2位??????????????????????????????????????C.?9位??????????????????????????????????????D.?10位
8.从九(1)班2名优秀班干部和九(2)班2名优秀班干部中,随机选取两名学生担任升旗手,则选取的两名升旗手不是同一个班的概率为(?? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
9.一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机选择一条路径,则它获取食物的概率是( )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
10.如图所示,小明、小刚利用两个转盘进行游戏,规则为小明将两个转盘各转一次,如配成紫色(红与蓝),小明胜,否则小刚胜,此规则(?? )
A.?公平????????????????????????B.?对小明有利????????????????????????C.?对小刚有利????????????????????????D.?公平性不可预测
二、填空题
11.一个不透明的盒子里放置三张完全相同的卡片,分别标有数字1,2,3.随机抽取1张,放回后再随机抽取1张,则抽得的第二张卡片上的数字大于第一张卡片上的数字的概率为________.
12.口袋内装有大小、质量和材料都相同的两种颜色的球,其中红色球3个,白色球2个,从中任意摸出一球,摸出白色球的概率是________.
13.在一个不透明的袋子中有 个红球、 个绿球和 个白球,这些球除颜色外都相同,摇匀后从袋子中任意摸出一个球,摸出________颜色的球的可能性最大.
14.桌子上有6杯同样型号的杯子,其中1杯白糖水,2杯矿泉水,3杯凉白开,从6个杯子中随机取出1杯,请你将下列事件发生的可能性从大到小排列:________ .(填序号即可)①取到凉白开 ②取到白糖水 ③取到矿泉水 ④没有取到矿泉水
15.向如图所示的正三角形区域扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形是等可能的,扔沙包1次击中阴影区域的概率等于________.
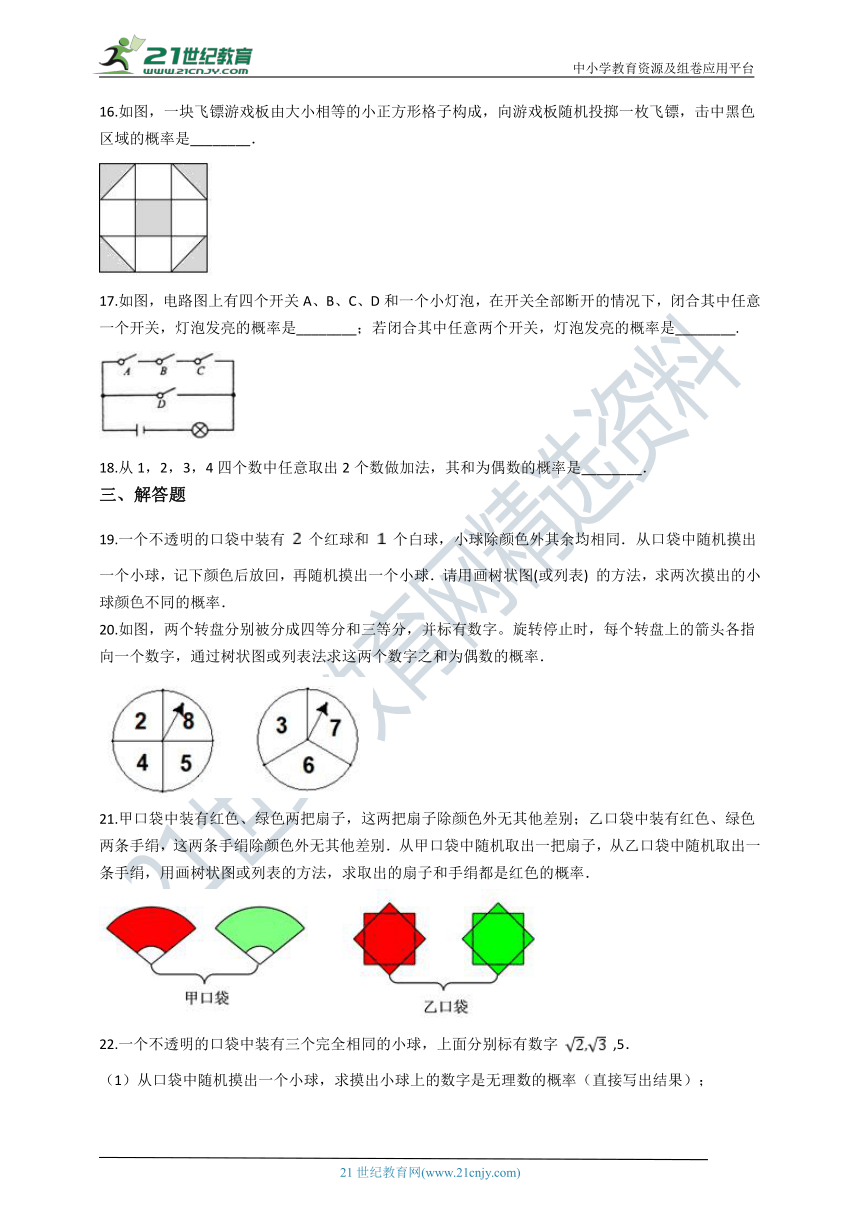
16.如图,一块飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是________.
17.如图,电路图上有四个开关A、B、C、D和一个小灯泡,在开关全部断开的情况下,闭合其中任意一个开关,灯泡发亮的概率是________;若闭合其中任意两个开关,灯泡发亮的概率是________.
18.从1,2,3,4四个数中任意取出2个数做加法,其和为偶数的概率是________.
三、解答题
19.一个不透明的口袋中装有 个红球和 个白球,小球除颜色外其余均相同.从口袋中随机摸出一个小球,记下颜色后放回,再随机摸出一个小球.请用画树状图(或列表) 的方法,求两次摸出的小球颜色不同的概率.
20.如图,两个转盘分别被分成四等分和三等分,并标有数字。旋转停止时,每个转盘上的箭头各指向一个数字,通过树状图或列表法求这两个数字之和为偶数的概率.
21.甲口袋中装有红色、绿色两把扇子,这两把扇子除颜色外无其他差别;乙口袋中装有红色、绿色两条手绢,这两条手绢除颜色外无其他差别.从甲口袋中随机取出一把扇子,从乙口袋中随机取出一条手绢,用画树状图或列表的方法,求取出的扇子和手绢都是红色的概率.
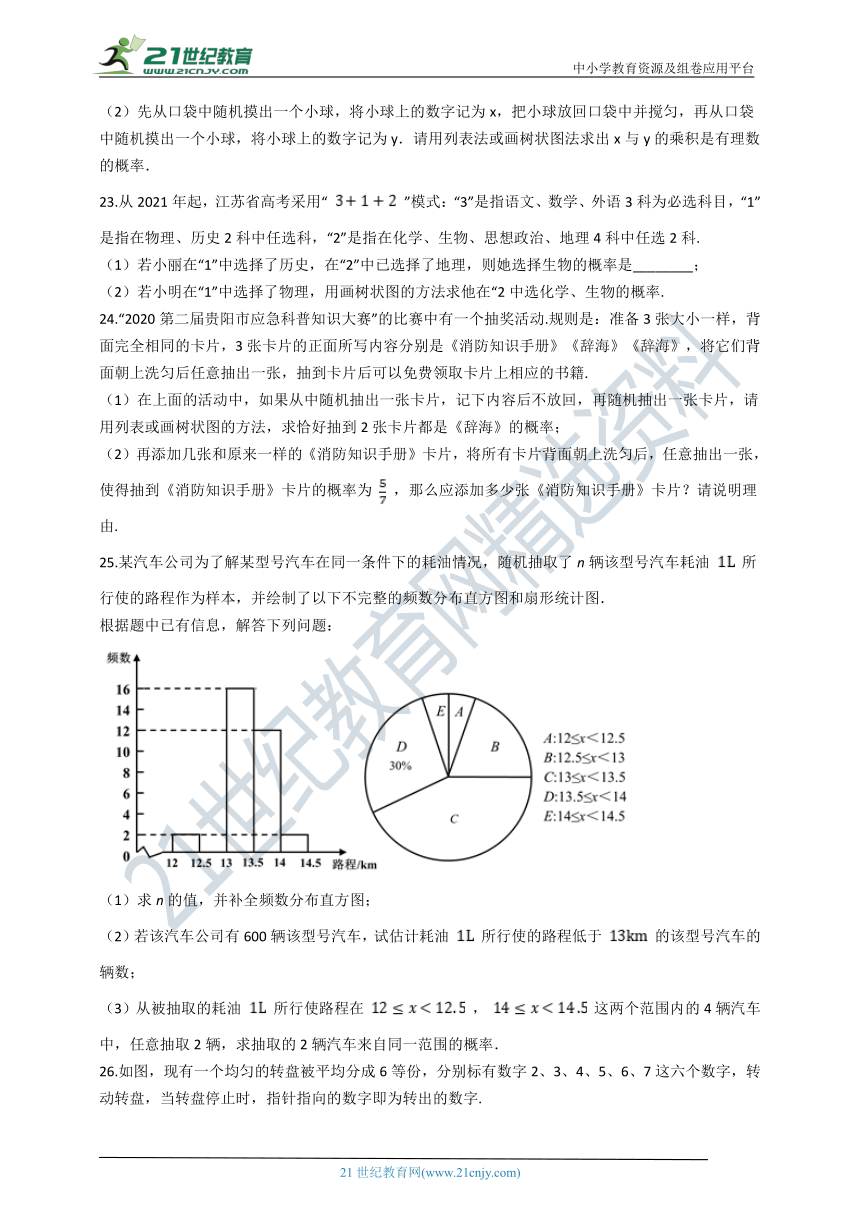
22.一个不透明的口袋中装有三个完全相同的小球,上面分别标有数字 ,5.
(1)从口袋中随机摸出一个小球,求摸出小球上的数字是无理数的概率(直接写出结果);
(2)先从口袋中随机摸出一个小球,将小球上的数字记为x,把小球放回口袋中并搅匀,再从口袋中随机摸出一个小球,将小球上的数字记为y.请用列表法或画树状图法求出x与y的乘积是有理数的概率.
23.从2021年起,江苏省高考采用“ ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
(1)若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是________;
(2)若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.
24.“2020第二届贵阳市应急科普知识大赛”的比赛中有一个抽奖活动.规则是:准备3张大小一样,背面完全相同的卡片,3张卡片的正面所写内容分别是《消防知识手册》《辞海》《辞海》,将它们背面朝上洗匀后任意抽出一张,抽到卡片后可以免费领取卡片上相应的书籍.
(1)在上面的活动中,如果从中随机抽出一张卡片,记下内容后不放回,再随机抽出一张卡片,请用列表或画树状图的方法,求恰好抽到2张卡片都是《辞海》的概率;
(2)再添加几张和原来一样的《消防知识手册》卡片,将所有卡片背面朝上洗匀后,任意抽出一张,使得抽到《消防知识手册》卡片的概率为 ,那么应添加多少张《消防知识手册》卡片?请说明理由.
25.某汽车公司为了解某型号汽车在同一条件下的耗油情况,随机抽取了n辆该型号汽车耗油 所行使的路程作为样本,并绘制了以下不完整的频数分布直方图和扇形统计图.
根据题中已有信息,解答下列问题:
(1)求n的值,并补全频数分布直方图;
(2)若该汽车公司有600辆该型号汽车,试估计耗油 所行使的路程低于 的该型号汽车的辆数;
(3)从被抽取的耗油 所行使路程在 , 这两个范围内的4辆汽车中,任意抽取2辆,求抽取的2辆汽车来自同一范围的概率.
26.如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
求:
(1)转动转盘,转出的数字大于3的概率是多少?
(2)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是________.
②这三条线段能构成等腰三角形的概率是________.
答案
一、选择题
1.① 掷得的点数是6,包含1种情况; ②掷得的点数是奇数,包含3种情况; ③掷得的点数不大于4,包含4种情况;④掷得的点数不小于2包含5中情况;
∴可能性大小顺序为:④③②①.
故选:B.
2.解:因为抛掷小正方体两次,每个面出现的机会是均等的:
A、得到的数字和有可能是4,A不符合题意;
B、得到的数字和有可能是3,B符合题意;
C、得到的数字和有可能是2,C不符合题意;
D、得到的数字和一定不可能是1,D不符合题意.
故答案为:B.
3.解:根据题意,电流在一定时间段内正常通过电子元件的概率是0.5,
即某一个电子元件不正常工作的概率为0.5,
则两个元件同时不正常工作的概率为0.25;
故在一定时间段内AB之间电流能够正常通过的概率为 =0.75,
故答案为:A.
4.解:∵随机抛掷一次,向下一面的数有1、2、3、4这4种等可能结果,其中向下一面数字是偶数的有2、4两种情况,
∴随机抛掷一次,向下一面的数是偶数的概率为 ,
故答案为:B.
5.解:大正方形的面积为:3×3=9,
阴影部分的面积为: ,
∴飞镖落在阴影部分的概率是:.
故答案为:C.
6.?∵袋子中有3个白球、2个黄球和1个红球,共6个小球,
∴从袋子中随机摸出一个球共有6种等可能结果,其中黄球有2种结果,
∴?从袋子中随机摸出一个球是黄球的概率为.
故答案为:B.
7.解:因为取一位数时一次就拨对密码的概率为 ,取两位数时一次就拨对密码的概率为 ,取三位数时一次就拨对密码的概率为 ,故密码的位数至少需要3位.
故答案为:3.
8.画树状图为:(用A、A表示九(1)班2名优秀班干部,用B、B表示九(2)班2名优秀班干部)
共有12种等可能的结果数,其中选取的两名升旗手不是同一个班的结果数为8,
所以选取的两名升旗手不是同一个班的概率= = .
故答案为:A.
9.解:根据树形图,可知
蚂蚁可选择的所有可能的路径有5条,有食物的两条,
所以它获取食物的概率是 .
故答案为:C.
10.解:如图:
根据树形图可知:
所有等可能的情况有8种,
其中配成紫色(红与蓝)的有3种,
所以
所以此规则对小刚有利.
故答案为:C .
二、填空题
11.解:分别从标有数字1、2、3的3张卡片中随机抽取1张,放回后再随机抽取1张,基本事件总数3×3=9,抽得的第二张卡片上的数字大于第一张卡片上的数字的情况有(1,2)、(1,3)和(2,3)3种情况
则抽得的第二张卡片上的数字大于第一张卡片上的数字的概率为: .
故答案为 .
12.由题可知,摸出白球的概率 .
故答案为 .
13.根据题意,袋子中共6个球,其中有1个红球,2个绿球和3个白球,故将球摇匀,从中任取1球,
①恰好取出红球的可能性为 ,
②恰好取出绿球的可能性为 ,
③恰好取出白球的可能性为 ,
摸出白颜色的球的可能性最大.
故答案是:白.
14.①取到凉白开的概率是 ;
②取到白糖水的概率是 ;
③取到矿泉水的概率是
④没有取到矿泉水的概率是
故发生的可能性从大到小排列为:④①③②
故填:④①③②.
15.解:由图可以看出,一共有最小规格的正三角形16个,其中涂黑了的有6个.有等可能的情况之下,扔沙包1次击中阴影区域的概率等于 .
故答案为: .
16.解:设小正方形边长为1,由图可知:∵.向游戏板随机投掷一枚飞镖,击中黑色区域的概率为: = .
故答案为: .
17.解:∵四个开关A、B、C、D和一个小灯泡,闭合开关D,灯泡发亮,
∴闭合其中任意一个开关,灯泡发亮的概率是;
若闭合其中任意两个开关,一共有AB,AC,AD,BC,BD,CD6种结果,
灯泡发亮的有AD,BD,CD,3种情况,
∴若闭合其中任意两个开关,灯泡发亮的概率是.
故答案为: , .
18. 解:如下表:
? 1 2 3 4
1 ? 1+2=3 1+3=4 1+4=5
2 1+2=3 ? 2+3=5 2+4=6
3 3+1=4 3+2=5 ? 4+3=7
4 4+1=5 4+2=6 4+3=7 ?
∴P(和为偶数)= .
三、解答题
19. 根据题意画出树状图如下:
?
所以 一共有9种情况,
两个小球颜色不相同的有4种, 所以,P(颜色不相同)=
20. 解:列表如下:
2 4 5 8
3 5 7 8 11
6 8 10 11 14
7 9 11 12 15
共有12种等可能结果数,和为偶数的有5个
所以 (和为偶数) .
21.解:画树状图如下:
共有4种可能结果,其中取出的扇子和手绢都是红色的有1种可能,
所以,所求的概率为:
22. (1)解:摸出小球上的数字是无理数的概率= ;
(2)解:画树状图如下:
可知:共有9种等可能的结果,其中两个数字的乘积为有理数的有3种,
∴两次摸出的小球所标数字乘积是有理数的概率为 = .
23.(1)
(2)解:列出树状图如图所示:
由图可知,共有12种可能结果,其中选化学、生物的有2种,
所以,P(选化学、生物) .
答:小明同学选化学、生物的概率是 .
24. (1)解:先将《消防知识手册》《辞海》《辞海》分别记作A, , ,然后列表如下:
第2次 第1次 A
A
总共有6种结果,每种结果出现的可能性相同,而2张卡片都是《辞海》的
有2种: ,
所以, (2张卡片都是《辞海》) ;
(2)解:设再添加x张和原来一样的《消防知识手册》卡片,由题意得:
,解得, ,
经检验, 是原方程的根,
答:应添加4张《消防知识手册》卡片.
25. (1)解:n=12÷30%=40(辆),
B:40-2-16-12-2=8,
补全频数分布直方图如下:
(2)解: =150(辆),
答:耗油 所行使的路程低于 的该型号汽车的有150辆;
(3)解:从被抽取的耗油 所行使路程在 的有2辆,记为A,B,行使路程在 的有2辆,记为1,2,任意抽取2辆的可能结果有6种,分别为:
(A,1),(A,2),(A,B),(B,1),(B,2),(1,2)
其中抽取的2辆汽车来自同一范围的的结果有2种,
所以抽取的2辆汽车来自同一范围的的概率P= = .
26. (1)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于3的结果有4种,
∴转出的数字大于3的概率是
(2);
(2)①转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成三角形的结果有5种,
∴这三条线段能构成三角形的概率是
②转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成等腰三角形的结果有2种,
∴这三条线段能构成等腰三角形的概率是
_21?????????è?????(www.21cnjy.com)_
2020年秋苏科版九年级数学上册第4章 等可能条件下的概率单元测试卷解析版
一、选择题
1.投掷一枚普通的正方体骰子,有下列事件:①掷得的点数是6;②掷得的点数是奇数;③掷得的点数不大于4;④掷得的点数不小于2,这些事件发生的可能性由大到小排列正确的是(?? ).
A.?①②③④???????????????????????????B.?④③②①???????????????????????????C.?③④②①???????????????????????????D.?②③①④
2.一个质地均匀的小正方体的六个面上分别标有数字1,2,3,4,5,6.如果任意抛掷小正方体两次,那么下列说法正确的是(?? ).
A.?得到的数字和必然是4?????????????????????????????????????????B.?得到的数字和可能是3
C.?得到的数字和不可能是2?????????????????????????????????????D.?得到的数字和有可能是1
3.已知电流在一定时间段内正常通过电子元件“ ”的概率是0.5;则在一定时间段内,由该元件组成的图示电路A、B之间,电流能够正常通过的概率是(??? )
A.?0.75?????????????????????????????????????B.?0.625?????????????????????????????????????C.?0.5?????????????????????????????????????D.?0.25
4.已知一个质地均匀的正四面体的每个面上分别标有1,2,3,4四个数字,抛掷这个正四面体,则接地的那一面为偶数的概率为(??? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
5.如图,飞镖游戏板中每一块小正方形除颜色外都相同。若一个人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是(??? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
6.一个不透明的袋子中有3个白球、2个黄球和1个红球,这些球除颜色外其他完全相同,那么从袋子中随机摸出一个球是黄球的概率为( ???)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
7.一个密码箱的密码,每个位数上的数都是从0到9的自然数,若要使不知道密码的一次就拨对密码的概率小于 ,则密码的位数至少需要(???? )位.
A.?3位??????????????????????????????????????B.?2位??????????????????????????????????????C.?9位??????????????????????????????????????D.?10位
8.从九(1)班2名优秀班干部和九(2)班2名优秀班干部中,随机选取两名学生担任升旗手,则选取的两名升旗手不是同一个班的概率为(?? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
9.一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机选择一条路径,则它获取食物的概率是( )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
10.如图所示,小明、小刚利用两个转盘进行游戏,规则为小明将两个转盘各转一次,如配成紫色(红与蓝),小明胜,否则小刚胜,此规则(?? )
A.?公平????????????????????????B.?对小明有利????????????????????????C.?对小刚有利????????????????????????D.?公平性不可预测
二、填空题
11.一个不透明的盒子里放置三张完全相同的卡片,分别标有数字1,2,3.随机抽取1张,放回后再随机抽取1张,则抽得的第二张卡片上的数字大于第一张卡片上的数字的概率为________.
12.口袋内装有大小、质量和材料都相同的两种颜色的球,其中红色球3个,白色球2个,从中任意摸出一球,摸出白色球的概率是________.
13.在一个不透明的袋子中有 个红球、 个绿球和 个白球,这些球除颜色外都相同,摇匀后从袋子中任意摸出一个球,摸出________颜色的球的可能性最大.
14.桌子上有6杯同样型号的杯子,其中1杯白糖水,2杯矿泉水,3杯凉白开,从6个杯子中随机取出1杯,请你将下列事件发生的可能性从大到小排列:________ .(填序号即可)①取到凉白开 ②取到白糖水 ③取到矿泉水 ④没有取到矿泉水
15.向如图所示的正三角形区域扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形是等可能的,扔沙包1次击中阴影区域的概率等于________.
16.如图,一块飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是________.
17.如图,电路图上有四个开关A、B、C、D和一个小灯泡,在开关全部断开的情况下,闭合其中任意一个开关,灯泡发亮的概率是________;若闭合其中任意两个开关,灯泡发亮的概率是________.
18.从1,2,3,4四个数中任意取出2个数做加法,其和为偶数的概率是________.
三、解答题
19.一个不透明的口袋中装有 个红球和 个白球,小球除颜色外其余均相同.从口袋中随机摸出一个小球,记下颜色后放回,再随机摸出一个小球.请用画树状图(或列表) 的方法,求两次摸出的小球颜色不同的概率.
20.如图,两个转盘分别被分成四等分和三等分,并标有数字。旋转停止时,每个转盘上的箭头各指向一个数字,通过树状图或列表法求这两个数字之和为偶数的概率.
21.甲口袋中装有红色、绿色两把扇子,这两把扇子除颜色外无其他差别;乙口袋中装有红色、绿色两条手绢,这两条手绢除颜色外无其他差别.从甲口袋中随机取出一把扇子,从乙口袋中随机取出一条手绢,用画树状图或列表的方法,求取出的扇子和手绢都是红色的概率.
22.一个不透明的口袋中装有三个完全相同的小球,上面分别标有数字 ,5.
(1)从口袋中随机摸出一个小球,求摸出小球上的数字是无理数的概率(直接写出结果);
(2)先从口袋中随机摸出一个小球,将小球上的数字记为x,把小球放回口袋中并搅匀,再从口袋中随机摸出一个小球,将小球上的数字记为y.请用列表法或画树状图法求出x与y的乘积是有理数的概率.
23.从2021年起,江苏省高考采用“ ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
(1)若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是________;
(2)若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.
24.“2020第二届贵阳市应急科普知识大赛”的比赛中有一个抽奖活动.规则是:准备3张大小一样,背面完全相同的卡片,3张卡片的正面所写内容分别是《消防知识手册》《辞海》《辞海》,将它们背面朝上洗匀后任意抽出一张,抽到卡片后可以免费领取卡片上相应的书籍.
(1)在上面的活动中,如果从中随机抽出一张卡片,记下内容后不放回,再随机抽出一张卡片,请用列表或画树状图的方法,求恰好抽到2张卡片都是《辞海》的概率;
(2)再添加几张和原来一样的《消防知识手册》卡片,将所有卡片背面朝上洗匀后,任意抽出一张,使得抽到《消防知识手册》卡片的概率为 ,那么应添加多少张《消防知识手册》卡片?请说明理由.
25.某汽车公司为了解某型号汽车在同一条件下的耗油情况,随机抽取了n辆该型号汽车耗油 所行使的路程作为样本,并绘制了以下不完整的频数分布直方图和扇形统计图.
根据题中已有信息,解答下列问题:
(1)求n的值,并补全频数分布直方图;
(2)若该汽车公司有600辆该型号汽车,试估计耗油 所行使的路程低于 的该型号汽车的辆数;
(3)从被抽取的耗油 所行使路程在 , 这两个范围内的4辆汽车中,任意抽取2辆,求抽取的2辆汽车来自同一范围的概率.
26.如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
求:
(1)转动转盘,转出的数字大于3的概率是多少?
(2)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是________.
②这三条线段能构成等腰三角形的概率是________.
答案
一、选择题
1.① 掷得的点数是6,包含1种情况; ②掷得的点数是奇数,包含3种情况; ③掷得的点数不大于4,包含4种情况;④掷得的点数不小于2包含5中情况;
∴可能性大小顺序为:④③②①.
故选:B.
2.解:因为抛掷小正方体两次,每个面出现的机会是均等的:
A、得到的数字和有可能是4,A不符合题意;
B、得到的数字和有可能是3,B符合题意;
C、得到的数字和有可能是2,C不符合题意;
D、得到的数字和一定不可能是1,D不符合题意.
故答案为:B.
3.解:根据题意,电流在一定时间段内正常通过电子元件的概率是0.5,
即某一个电子元件不正常工作的概率为0.5,
则两个元件同时不正常工作的概率为0.25;
故在一定时间段内AB之间电流能够正常通过的概率为 =0.75,
故答案为:A.
4.解:∵随机抛掷一次,向下一面的数有1、2、3、4这4种等可能结果,其中向下一面数字是偶数的有2、4两种情况,
∴随机抛掷一次,向下一面的数是偶数的概率为 ,
故答案为:B.
5.解:大正方形的面积为:3×3=9,
阴影部分的面积为: ,
∴飞镖落在阴影部分的概率是:.
故答案为:C.
6.?∵袋子中有3个白球、2个黄球和1个红球,共6个小球,
∴从袋子中随机摸出一个球共有6种等可能结果,其中黄球有2种结果,
∴?从袋子中随机摸出一个球是黄球的概率为.
故答案为:B.
7.解:因为取一位数时一次就拨对密码的概率为 ,取两位数时一次就拨对密码的概率为 ,取三位数时一次就拨对密码的概率为 ,故密码的位数至少需要3位.
故答案为:3.
8.画树状图为:(用A、A表示九(1)班2名优秀班干部,用B、B表示九(2)班2名优秀班干部)
共有12种等可能的结果数,其中选取的两名升旗手不是同一个班的结果数为8,
所以选取的两名升旗手不是同一个班的概率= = .
故答案为:A.
9.解:根据树形图,可知
蚂蚁可选择的所有可能的路径有5条,有食物的两条,
所以它获取食物的概率是 .
故答案为:C.
10.解:如图:
根据树形图可知:
所有等可能的情况有8种,
其中配成紫色(红与蓝)的有3种,
所以
所以此规则对小刚有利.
故答案为:C .
二、填空题
11.解:分别从标有数字1、2、3的3张卡片中随机抽取1张,放回后再随机抽取1张,基本事件总数3×3=9,抽得的第二张卡片上的数字大于第一张卡片上的数字的情况有(1,2)、(1,3)和(2,3)3种情况
则抽得的第二张卡片上的数字大于第一张卡片上的数字的概率为: .
故答案为 .
12.由题可知,摸出白球的概率 .
故答案为 .
13.根据题意,袋子中共6个球,其中有1个红球,2个绿球和3个白球,故将球摇匀,从中任取1球,
①恰好取出红球的可能性为 ,
②恰好取出绿球的可能性为 ,
③恰好取出白球的可能性为 ,
摸出白颜色的球的可能性最大.
故答案是:白.
14.①取到凉白开的概率是 ;
②取到白糖水的概率是 ;
③取到矿泉水的概率是
④没有取到矿泉水的概率是
故发生的可能性从大到小排列为:④①③②
故填:④①③②.
15.解:由图可以看出,一共有最小规格的正三角形16个,其中涂黑了的有6个.有等可能的情况之下,扔沙包1次击中阴影区域的概率等于 .
故答案为: .
16.解:设小正方形边长为1,由图可知:∵.向游戏板随机投掷一枚飞镖,击中黑色区域的概率为: = .
故答案为: .
17.解:∵四个开关A、B、C、D和一个小灯泡,闭合开关D,灯泡发亮,
∴闭合其中任意一个开关,灯泡发亮的概率是;
若闭合其中任意两个开关,一共有AB,AC,AD,BC,BD,CD6种结果,
灯泡发亮的有AD,BD,CD,3种情况,
∴若闭合其中任意两个开关,灯泡发亮的概率是.
故答案为: , .
18. 解:如下表:
? 1 2 3 4
1 ? 1+2=3 1+3=4 1+4=5
2 1+2=3 ? 2+3=5 2+4=6
3 3+1=4 3+2=5 ? 4+3=7
4 4+1=5 4+2=6 4+3=7 ?
∴P(和为偶数)= .
三、解答题
19. 根据题意画出树状图如下:
?
所以 一共有9种情况,
两个小球颜色不相同的有4种, 所以,P(颜色不相同)=
20. 解:列表如下:
2 4 5 8
3 5 7 8 11
6 8 10 11 14
7 9 11 12 15
共有12种等可能结果数,和为偶数的有5个
所以 (和为偶数) .
21.解:画树状图如下:
共有4种可能结果,其中取出的扇子和手绢都是红色的有1种可能,
所以,所求的概率为:
22. (1)解:摸出小球上的数字是无理数的概率= ;
(2)解:画树状图如下:
可知:共有9种等可能的结果,其中两个数字的乘积为有理数的有3种,
∴两次摸出的小球所标数字乘积是有理数的概率为 = .
23.(1)
(2)解:列出树状图如图所示:
由图可知,共有12种可能结果,其中选化学、生物的有2种,
所以,P(选化学、生物) .
答:小明同学选化学、生物的概率是 .
24. (1)解:先将《消防知识手册》《辞海》《辞海》分别记作A, , ,然后列表如下:
第2次 第1次 A
A
总共有6种结果,每种结果出现的可能性相同,而2张卡片都是《辞海》的
有2种: ,
所以, (2张卡片都是《辞海》) ;
(2)解:设再添加x张和原来一样的《消防知识手册》卡片,由题意得:
,解得, ,
经检验, 是原方程的根,
答:应添加4张《消防知识手册》卡片.
25. (1)解:n=12÷30%=40(辆),
B:40-2-16-12-2=8,
补全频数分布直方图如下:
(2)解: =150(辆),
答:耗油 所行使的路程低于 的该型号汽车的有150辆;
(3)解:从被抽取的耗油 所行使路程在 的有2辆,记为A,B,行使路程在 的有2辆,记为1,2,任意抽取2辆的可能结果有6种,分别为:
(A,1),(A,2),(A,B),(B,1),(B,2),(1,2)
其中抽取的2辆汽车来自同一范围的的结果有2种,
所以抽取的2辆汽车来自同一范围的的概率P= = .
26. (1)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于3的结果有4种,
∴转出的数字大于3的概率是
(2);
(2)①转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成三角形的结果有5种,
∴这三条线段能构成三角形的概率是
②转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成等腰三角形的结果有2种,
∴这三条线段能构成等腰三角形的概率是
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
