2020年秋苏科版八年级数学上册 第三章 勾股定理单元测试卷(含解析)
文档属性
| 名称 | 2020年秋苏科版八年级数学上册 第三章 勾股定理单元测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 20:55:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020年秋苏科版八年级数学上册第三章 勾股定理单元测试卷
一、选择题(共10题;共30分)
1.在△ABC,∠A,∠B,∠C的对应边分别是a,b,c,若∠B=90°,则下列等式中成立的是(???? )
A.?a2+b2=c2 ???????????????????????B.?b2+c2=a2???????????????????????C.??? a2+c2=b2???????????????????????D.?c2- a2= b2
2.由线段 组成的三角形不是直角三角形的是(?? )
A.?????? B.??????
C.?????? D.?
3.直角三角形中,两条直角边长分别是12和5,则斜边中线长是(?? )
A.?26????????????????????????????????????????B.?13????????????????????????????????????????C.?????????????????????????????????????????D.?6.5
4.古代数学的“折竹抵地”问题:“今有竹高九尺,末折抵地,去本三尺,问折者高几何?”意思是:现有竹子高9尺,折后竹尖抵地与竹子底部的距离为3尺,问折处高几尺?即:如图,AB+AC=9尺,BC=3尺,则AC等于(??? )尺.
A.?3.5??????????????????????????????????????????B.?4??????????????????????????????????????????C.?4.5??????????????????????????????????????????D.?5
5.以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形A的面积为(?? )
A.?6??????????????????????????????????????????B.?36??????????????????????????????????????????C.?64??????????????????????????????????????????D.?8
6.如图所示,有一个高 ,底面周长为 的圆柱形玻璃容器,在外侧距下底 的点 处有一只蚂蚁,与蚂蚁相对的圆柱形容器的上口内侧距开口处 的点 处有一滴凝固的蜂蜜,则蚂蚁到凝固蜂蜜所走的最短路径的长度是(? )
A.????????????????????????????????????????B.?20???????????????????????????????????????C.?24???????????????????????????????????????D.?28
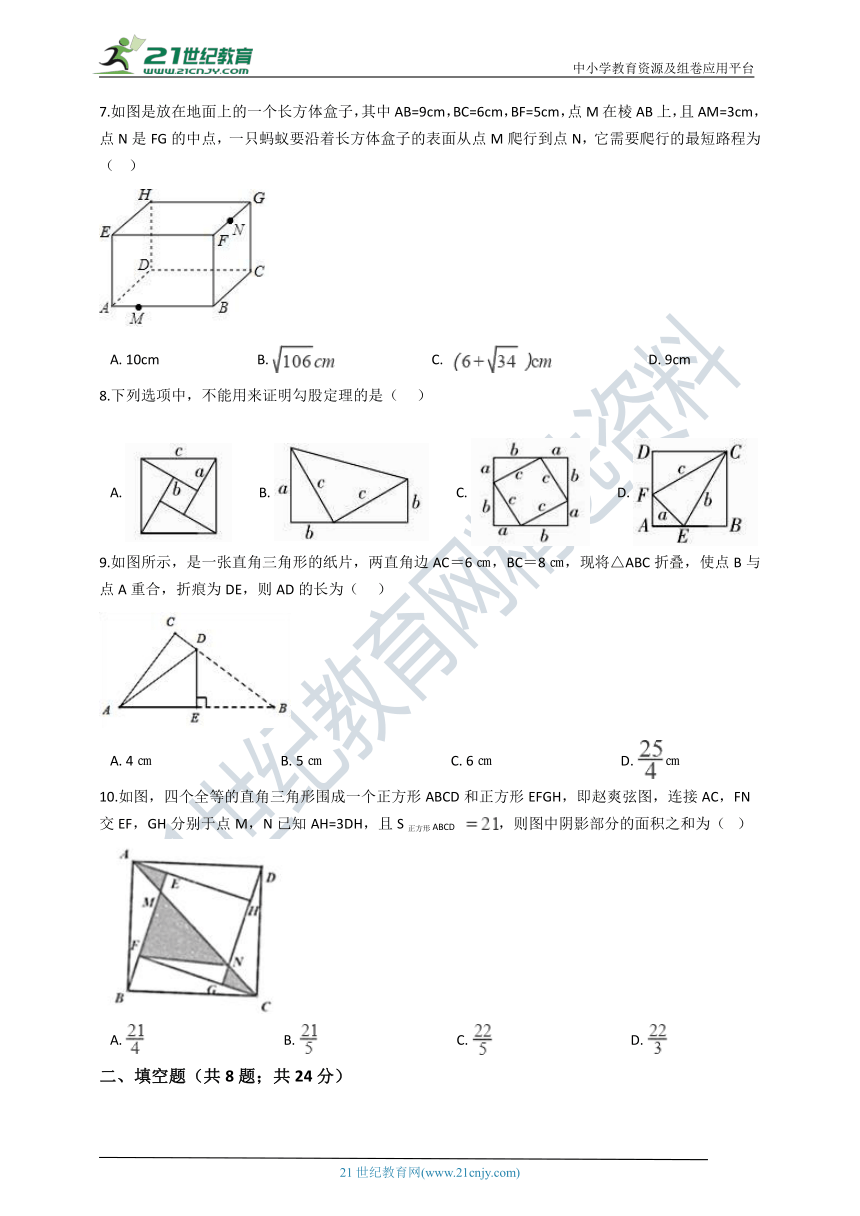
7.如图是放在地面上的一个长方体盒子,其中AB=9cm,BC=6cm,BF=5cm,点M在棱AB上,且AM=3cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为(?? )
A.?10cm????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?9cm
8.下列选项中,不能用来证明勾股定理的是(??? )
A.?????????B.?????????C.?????????D.?
9.如图所示,是一张直角三角形的纸片,两直角边AC=6㎝,BC=8㎝,现将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为(??? )
A.?4㎝?????????????????????????????????????B.?5㎝?????????????????????????????????????C.?6㎝?????????????????????????????????????D.?㎝
10.如图,四个全等的直角三角形围成一个正方形ABCD和正方形EFGH,即赵爽弦图,连接AC,FN交EF,GH分别于点M,N已知AH=3DH,且S正方形ABCD ,则图中阴影部分的面积之和为(? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
二、填空题(共8题;共24分)
11.如图,为修铁路需凿通隧道BC , 测得∠C=90°,AB=5km , AC=4km , 若每天凿隧道0.3km , 则需________天才能把隧道凿通.
12.有一个三角形的两边长是9和12,要使这个三角形成为直角三角形,则第三条边长的平方是________.
13.如图,在 中, , ,分别以点A和B为圆心,以大于 的长为半径作弧,两弧相交于点M和N,作直线 ,交 于点E,连接 ,若 ,则 的长为________.
14.在 中, ,若 ,则 的长是________.
15.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=2,BC=4,则AB2+CD2=________.
16.如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(片在结合部分不重叠无缝隙),则图2中阴影部分面积为________。
17.如图,所有阴影四边形都是正方形,两个空白三角形均为直角三角形,且A、B、C三个正方形的边长分别为2、3、4,则正方形D的面积为________.
18.如图, , , ,一机器人在点B处看见一个小球从点A出发沿着 方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC为________.
三、解答题(共7题;共46分)
19.已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.
20.如图,一高层住宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面2米,问:发生火灾的住户窗口距离地面多高?
21.如图,AB⊥BC,CD⊥BC,点E在BC上,且AE=DE. 若AB=20,CD=30,BC=50,求AE的长.
22.如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.求:四边形ABDC的面积.
23.如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90,点A,C,D依次在同一直线上,且AB平行DE.
(1)求证:△ABC≌△DCE
(2)连结AE,当BC=5,AC=12时,求AE的长.
24.如图,已知正方体纸盒的表面积为12cm2;
(1)求正方体的棱长;
(2)剪去盖子后,插入一根长为5cm的细木棒,则细木棒露在外面的最短长度是多少?
(3)一只蚂蚁在纸盒的表面由A爬到B,求蚂蚁行走的最短路线.
25.教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为 ,较小的直角边长都为 ,斜边长都为 ),大正方形的面积可以表示为 ,也可以表示为 ,由此推导出重要的勾股定理:如果直角三角形两条直角边长为 ,斜边长为 ,则 .
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在 中, 是 边上的高, , , ,设 ,求 的值.
(3)试构造一个图形,使它的面积能够解释 ,画在如图4的网格中,并标出字母 所表示的线段.
答案
一、选择题
1.解:∵∠B=90°,
∴ a2+c2=b2?.
故答案为:C.
2.解:A、32+42=52 , 符合勾股定理的逆定理,是直角三角形;
B、82+92≠102不符合勾股定理的逆定理,不是直角三角形;
C、82+152=172 , 符合勾股定理的逆定理,是直角三角形;
D、52+122=132 , 符合勾股定理的逆定理,是直角三角形.
故答案为:B.
3.解:∵直角三角形中,两直角边长分别为12和5,
∴斜边= =13,
则斜边中线长是6.5,
故答案为:D.
4.解:设竹子折断处离地面AC=x尺,则斜边为AB=(9-x)尺,根据勾股定理得:
解得:x=4,
∴AC=4尺.
故答案为:B.
5.解:根据直角三角形的勾股定理,两直角边的平方和等于斜边的平方,三角形边长的平方即为正方形的面积,故8+A=14,A=6;
故答案为:A。
6.如图:
过F点作容器上沿的对称点B,过S作SC⊥BC于C,
连接SB,则SB即为最短距离,
由题意得:SC为圆柱体的底面周长的一半, (cm),
FD=BD=2,
∴B (cm),
∴ .
故答案为:B.
7.如图1.
∵AB=9cm,BC=GF=6cm,BF=5cm,∴BM=9﹣3=6,BN=5+3=8,∴MN= =10;
如图2.∵AB=9cm,BC=GF=6cm,BF=5cm,∴PM=6+3=9,NP=5,∴MN= = .
∵10< ,∴蚂蚁沿长方体表面爬到米粒处的最短距离为10.
故答案为:A.
8.A.∵四个直角三角形面积+小正方形面积=大正方形面积,∴ ,整理得: ,可以证明勾股定理;
B.∵三个直角三角形的面积和=梯形面积,∴ ,整理得: ,可以证明勾股定理;
C.∵四个直角三角形面积+小正方形面积=大正方形面积,∴ ,整理得: ,可以证明勾股定理;
D.不能利用图形面积证明勾股定理,故此选项符合题意.
故答案为:D.
9.设AD=xcm,
由折叠的性质得:BD=AD=xcm,
∵在Rt△ABC中,AC=6cm,BC=8cm,
∴CD=BC?BD=8?x(cm),AB=10cm,
在Rt△ACD中,AC +CD =AD ,
即:6 +(8?x) =x ,
解得:x= .
故答案为:D.
10解:∵AH=3DH,且S正方形ABCD ,
∴AH2+DH2=AD2=21
即(3DH)2+DH2=21
解得:DH= ,
∴AH=
由全等三角形的性质可得AE=DH=CG= ,CG:FG=AE:EH=1:2
∴正方形EFGH的边长EH=AH-AE= ,S△FGN=2S△CGN
∵AH∥CF
∴∠HEN=∠FCM
∵∠AEM=∠CGN=90°,AE=CG,∠AHN=∠CFM=90°,AH=CF
∴ AEM≌ CGN, AHN≌ CFM
∴S△AEM= S△CGN , S△AHN = S△CFM
∴S四边形MFGN= S△CFM-S△CGN= S△AHN-S△AEM=S四边形EMNH= S正方形EFGH= × =
∵S△FGN=2S△CGN
∴S阴影=S△MNF+S△AEM+S△CGN
= S△MNF+2S△CGN
= S△MNF+S△FGN
= S四边形MFGN
=
故答案为:B.
二、填空题
11.解:根据题意,
∵∠C=90°,AB=5km , AC=4km ,
则由勾股定理,得 ,
∴所需的时间为: (天);
故答案为:10.
12.解:当第三边是斜边时,第三边的长的平方是:92+122=225;
当第三边是直角边时,第三边长的平方是:122-92=144-81=63;
故答案是:225或63.
13.解:由题意得MN垂直平分AB,∴AE=BE,
设BE=AE=x,∴AC=CE+AE=x+3,
∵AC=2BC,∴BC=,
在Rt△BCE中,BC2+CE2=BE2 ,
即()2+32=x2 , 解得x1=5,x2=-3(舍去),
∴BE=5.
故答案为:5.
14.解:∵在Rt△ABC中,∠C=90°,AB-AC=2,BC=8,
∴AC2+BC2=AB2 ,
即(AB-2)2+82=AB2 ,
解得AB=17.
故答案为:17.
15.解:∵AC⊥BD,
∵AD2=OA2+OD2 , AB2=OA2+OB2 , CD2=OC2+OD2 , BC2=OB2+OC2 ,
∴AD2+BC2=AB2+CD2=OA2+OB2+OC2+OD2
=22+42=20.
故答案为:20.
16解:由题意可得,
直角三角形的斜边长为3,一条直角边长为2,
故直角三角形的另一条直角边长为: ,
故阴影部分的面积是: ,
故答案为: .
17.解:设正方形A,B,C,D的边长分别为a,b,c,d,根据勾股定理得
,
∵正方形A、B、C的面积依次为2、4、3,
∴根据图形得:2+4= ﹣3,
解得: =9,
故答案为:9.
18.解:∵小球滚动的速度与机器人行走的速度相等,
∴BC=AC,
设BC=AC=xm,
则OC=(9-x)m,
在Rt△BOC中,
∵OB2+OC2=BC2 ,
∴32+(9-x)2=x2 ,
解得x=5.
故答案为:5m.
三、解答题
19.解:在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,
由勾股定理得:AB=? =10,
∵S△ABC= AB?CD= AC?BC,
∴CD= = =4.8
20. 解:由题意,AB=15,AC=DE=9,CD=AE=2,BD⊥AC,
在Rt△ACB中,由勾股定理得:
,
∴BD=BC+CD=14(米),
答:发生火灾的住户窗口距离地面14米.
21. 解:设BE=x,则EC=50-x.
在Rt△ABE中,AE2=AB2+BE2=400+x2
在Rt△DCE中,DE2=CD2+CE2=900+(50-x)2
∵AE=DE,∴400+x2=900+(50-x)2
∴x=30.
∴AE2=400+x2=1300,∴AE= .
22. 解:∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,
∴BC= = =5;
∵在△BCD中,CD=4,BD=3,BC=5,
∴CD2+BD2=BC2 ,
∴△BCD是直角三角形,
∴四边形ABDC的面积=S△ABC+S△BCD= ×12×5+ ×3×4=36.
23. (1)证明:∵AB∥DE,
∴∠BAC=∠CDE,
在△ABC和△DCE中,
,
∴△ABC≌△DCE(AAS);
(2)解:∵△ABC≌△DCE,
∴CE=BC=5,
∴AE==13.
24. (1)解:正方体有六个表面,表面积为 .
每个表面的面积为 ;
设棱长为为xcm( ),即 ,
∴ ,
即棱长为 ;
(2)解:如图1所示:
由题意知:插入细木棒后,看不见的部分恰好是正方体的对角线 ,
∵
;
又∵ ,
,
则细木棒露在外面的最短长度为 .
(3)解:如图2所示:
在Rt△AGB中,AG=GD=DB= ,AB= ,
蚂蚁爬行的路径 ,
蚂蚁爬行的最短距离是 .
25. (1)解:梯形 的面积为 ,
也可以表示为 ,
,
即
(2)解:在 中,
在 中,
所以 ,
解得
(3)解:∵图形面积为:(a+b)(a+2b)=a?+3ab+b?
∴边长为:(a+b),(a+2b)
由此可画出的图形为:
_21?????????è?????(www.21cnjy.com)_
2020年秋苏科版八年级数学上册第三章 勾股定理单元测试卷
一、选择题(共10题;共30分)
1.在△ABC,∠A,∠B,∠C的对应边分别是a,b,c,若∠B=90°,则下列等式中成立的是(???? )
A.?a2+b2=c2 ???????????????????????B.?b2+c2=a2???????????????????????C.??? a2+c2=b2???????????????????????D.?c2- a2= b2
2.由线段 组成的三角形不是直角三角形的是(?? )
A.?????? B.??????
C.?????? D.?
3.直角三角形中,两条直角边长分别是12和5,则斜边中线长是(?? )
A.?26????????????????????????????????????????B.?13????????????????????????????????????????C.?????????????????????????????????????????D.?6.5
4.古代数学的“折竹抵地”问题:“今有竹高九尺,末折抵地,去本三尺,问折者高几何?”意思是:现有竹子高9尺,折后竹尖抵地与竹子底部的距离为3尺,问折处高几尺?即:如图,AB+AC=9尺,BC=3尺,则AC等于(??? )尺.
A.?3.5??????????????????????????????????????????B.?4??????????????????????????????????????????C.?4.5??????????????????????????????????????????D.?5
5.以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形A的面积为(?? )
A.?6??????????????????????????????????????????B.?36??????????????????????????????????????????C.?64??????????????????????????????????????????D.?8
6.如图所示,有一个高 ,底面周长为 的圆柱形玻璃容器,在外侧距下底 的点 处有一只蚂蚁,与蚂蚁相对的圆柱形容器的上口内侧距开口处 的点 处有一滴凝固的蜂蜜,则蚂蚁到凝固蜂蜜所走的最短路径的长度是(? )
A.????????????????????????????????????????B.?20???????????????????????????????????????C.?24???????????????????????????????????????D.?28
7.如图是放在地面上的一个长方体盒子,其中AB=9cm,BC=6cm,BF=5cm,点M在棱AB上,且AM=3cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为(?? )
A.?10cm????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?9cm
8.下列选项中,不能用来证明勾股定理的是(??? )
A.?????????B.?????????C.?????????D.?
9.如图所示,是一张直角三角形的纸片,两直角边AC=6㎝,BC=8㎝,现将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为(??? )
A.?4㎝?????????????????????????????????????B.?5㎝?????????????????????????????????????C.?6㎝?????????????????????????????????????D.?㎝
10.如图,四个全等的直角三角形围成一个正方形ABCD和正方形EFGH,即赵爽弦图,连接AC,FN交EF,GH分别于点M,N已知AH=3DH,且S正方形ABCD ,则图中阴影部分的面积之和为(? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
二、填空题(共8题;共24分)
11.如图,为修铁路需凿通隧道BC , 测得∠C=90°,AB=5km , AC=4km , 若每天凿隧道0.3km , 则需________天才能把隧道凿通.
12.有一个三角形的两边长是9和12,要使这个三角形成为直角三角形,则第三条边长的平方是________.
13.如图,在 中, , ,分别以点A和B为圆心,以大于 的长为半径作弧,两弧相交于点M和N,作直线 ,交 于点E,连接 ,若 ,则 的长为________.
14.在 中, ,若 ,则 的长是________.
15.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=2,BC=4,则AB2+CD2=________.
16.如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(片在结合部分不重叠无缝隙),则图2中阴影部分面积为________。
17.如图,所有阴影四边形都是正方形,两个空白三角形均为直角三角形,且A、B、C三个正方形的边长分别为2、3、4,则正方形D的面积为________.
18.如图, , , ,一机器人在点B处看见一个小球从点A出发沿着 方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC为________.
三、解答题(共7题;共46分)
19.已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.
20.如图,一高层住宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面2米,问:发生火灾的住户窗口距离地面多高?
21.如图,AB⊥BC,CD⊥BC,点E在BC上,且AE=DE. 若AB=20,CD=30,BC=50,求AE的长.
22.如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.求:四边形ABDC的面积.
23.如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90,点A,C,D依次在同一直线上,且AB平行DE.
(1)求证:△ABC≌△DCE
(2)连结AE,当BC=5,AC=12时,求AE的长.
24.如图,已知正方体纸盒的表面积为12cm2;
(1)求正方体的棱长;
(2)剪去盖子后,插入一根长为5cm的细木棒,则细木棒露在外面的最短长度是多少?
(3)一只蚂蚁在纸盒的表面由A爬到B,求蚂蚁行走的最短路线.
25.教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为 ,较小的直角边长都为 ,斜边长都为 ),大正方形的面积可以表示为 ,也可以表示为 ,由此推导出重要的勾股定理:如果直角三角形两条直角边长为 ,斜边长为 ,则 .
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在 中, 是 边上的高, , , ,设 ,求 的值.
(3)试构造一个图形,使它的面积能够解释 ,画在如图4的网格中,并标出字母 所表示的线段.
答案
一、选择题
1.解:∵∠B=90°,
∴ a2+c2=b2?.
故答案为:C.
2.解:A、32+42=52 , 符合勾股定理的逆定理,是直角三角形;
B、82+92≠102不符合勾股定理的逆定理,不是直角三角形;
C、82+152=172 , 符合勾股定理的逆定理,是直角三角形;
D、52+122=132 , 符合勾股定理的逆定理,是直角三角形.
故答案为:B.
3.解:∵直角三角形中,两直角边长分别为12和5,
∴斜边= =13,
则斜边中线长是6.5,
故答案为:D.
4.解:设竹子折断处离地面AC=x尺,则斜边为AB=(9-x)尺,根据勾股定理得:
解得:x=4,
∴AC=4尺.
故答案为:B.
5.解:根据直角三角形的勾股定理,两直角边的平方和等于斜边的平方,三角形边长的平方即为正方形的面积,故8+A=14,A=6;
故答案为:A。
6.如图:
过F点作容器上沿的对称点B,过S作SC⊥BC于C,
连接SB,则SB即为最短距离,
由题意得:SC为圆柱体的底面周长的一半, (cm),
FD=BD=2,
∴B (cm),
∴ .
故答案为:B.
7.如图1.
∵AB=9cm,BC=GF=6cm,BF=5cm,∴BM=9﹣3=6,BN=5+3=8,∴MN= =10;
如图2.∵AB=9cm,BC=GF=6cm,BF=5cm,∴PM=6+3=9,NP=5,∴MN= = .
∵10< ,∴蚂蚁沿长方体表面爬到米粒处的最短距离为10.
故答案为:A.
8.A.∵四个直角三角形面积+小正方形面积=大正方形面积,∴ ,整理得: ,可以证明勾股定理;
B.∵三个直角三角形的面积和=梯形面积,∴ ,整理得: ,可以证明勾股定理;
C.∵四个直角三角形面积+小正方形面积=大正方形面积,∴ ,整理得: ,可以证明勾股定理;
D.不能利用图形面积证明勾股定理,故此选项符合题意.
故答案为:D.
9.设AD=xcm,
由折叠的性质得:BD=AD=xcm,
∵在Rt△ABC中,AC=6cm,BC=8cm,
∴CD=BC?BD=8?x(cm),AB=10cm,
在Rt△ACD中,AC +CD =AD ,
即:6 +(8?x) =x ,
解得:x= .
故答案为:D.
10解:∵AH=3DH,且S正方形ABCD ,
∴AH2+DH2=AD2=21
即(3DH)2+DH2=21
解得:DH= ,
∴AH=
由全等三角形的性质可得AE=DH=CG= ,CG:FG=AE:EH=1:2
∴正方形EFGH的边长EH=AH-AE= ,S△FGN=2S△CGN
∵AH∥CF
∴∠HEN=∠FCM
∵∠AEM=∠CGN=90°,AE=CG,∠AHN=∠CFM=90°,AH=CF
∴ AEM≌ CGN, AHN≌ CFM
∴S△AEM= S△CGN , S△AHN = S△CFM
∴S四边形MFGN= S△CFM-S△CGN= S△AHN-S△AEM=S四边形EMNH= S正方形EFGH= × =
∵S△FGN=2S△CGN
∴S阴影=S△MNF+S△AEM+S△CGN
= S△MNF+2S△CGN
= S△MNF+S△FGN
= S四边形MFGN
=
故答案为:B.
二、填空题
11.解:根据题意,
∵∠C=90°,AB=5km , AC=4km ,
则由勾股定理,得 ,
∴所需的时间为: (天);
故答案为:10.
12.解:当第三边是斜边时,第三边的长的平方是:92+122=225;
当第三边是直角边时,第三边长的平方是:122-92=144-81=63;
故答案是:225或63.
13.解:由题意得MN垂直平分AB,∴AE=BE,
设BE=AE=x,∴AC=CE+AE=x+3,
∵AC=2BC,∴BC=,
在Rt△BCE中,BC2+CE2=BE2 ,
即()2+32=x2 , 解得x1=5,x2=-3(舍去),
∴BE=5.
故答案为:5.
14.解:∵在Rt△ABC中,∠C=90°,AB-AC=2,BC=8,
∴AC2+BC2=AB2 ,
即(AB-2)2+82=AB2 ,
解得AB=17.
故答案为:17.
15.解:∵AC⊥BD,
∵AD2=OA2+OD2 , AB2=OA2+OB2 , CD2=OC2+OD2 , BC2=OB2+OC2 ,
∴AD2+BC2=AB2+CD2=OA2+OB2+OC2+OD2
=22+42=20.
故答案为:20.
16解:由题意可得,
直角三角形的斜边长为3,一条直角边长为2,
故直角三角形的另一条直角边长为: ,
故阴影部分的面积是: ,
故答案为: .
17.解:设正方形A,B,C,D的边长分别为a,b,c,d,根据勾股定理得
,
∵正方形A、B、C的面积依次为2、4、3,
∴根据图形得:2+4= ﹣3,
解得: =9,
故答案为:9.
18.解:∵小球滚动的速度与机器人行走的速度相等,
∴BC=AC,
设BC=AC=xm,
则OC=(9-x)m,
在Rt△BOC中,
∵OB2+OC2=BC2 ,
∴32+(9-x)2=x2 ,
解得x=5.
故答案为:5m.
三、解答题
19.解:在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,
由勾股定理得:AB=? =10,
∵S△ABC= AB?CD= AC?BC,
∴CD= = =4.8
20. 解:由题意,AB=15,AC=DE=9,CD=AE=2,BD⊥AC,
在Rt△ACB中,由勾股定理得:
,
∴BD=BC+CD=14(米),
答:发生火灾的住户窗口距离地面14米.
21. 解:设BE=x,则EC=50-x.
在Rt△ABE中,AE2=AB2+BE2=400+x2
在Rt△DCE中,DE2=CD2+CE2=900+(50-x)2
∵AE=DE,∴400+x2=900+(50-x)2
∴x=30.
∴AE2=400+x2=1300,∴AE= .
22. 解:∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,
∴BC= = =5;
∵在△BCD中,CD=4,BD=3,BC=5,
∴CD2+BD2=BC2 ,
∴△BCD是直角三角形,
∴四边形ABDC的面积=S△ABC+S△BCD= ×12×5+ ×3×4=36.
23. (1)证明:∵AB∥DE,
∴∠BAC=∠CDE,
在△ABC和△DCE中,
,
∴△ABC≌△DCE(AAS);
(2)解:∵△ABC≌△DCE,
∴CE=BC=5,
∴AE==13.
24. (1)解:正方体有六个表面,表面积为 .
每个表面的面积为 ;
设棱长为为xcm( ),即 ,
∴ ,
即棱长为 ;
(2)解:如图1所示:
由题意知:插入细木棒后,看不见的部分恰好是正方体的对角线 ,
∵
;
又∵ ,
,
则细木棒露在外面的最短长度为 .
(3)解:如图2所示:
在Rt△AGB中,AG=GD=DB= ,AB= ,
蚂蚁爬行的路径 ,
蚂蚁爬行的最短距离是 .
25. (1)解:梯形 的面积为 ,
也可以表示为 ,
,
即
(2)解:在 中,
在 中,
所以 ,
解得
(3)解:∵图形面积为:(a+b)(a+2b)=a?+3ab+b?
∴边长为:(a+b),(a+2b)
由此可画出的图形为:
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
