2020年苏科版八年级数学上册 第五章 平面直角坐标系单元测试卷(含解析)
文档属性
| 名称 | 2020年苏科版八年级数学上册 第五章 平面直角坐标系单元测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 21:02:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020年苏科版八年级数学上册第五章 平面直角坐标系单元测试卷解析版
一、选择题(共10题;共30分)
1.小李、小王、小张、小谢原有位置如图(横为排、竖为列),小李在第2排第4列,小王在第3排第3列,小张在第4排第2列,小谢在第5排第4列.撤走第一排,仍按照原有确定位置的方法确定新的位置,下列说法正确的是(?? ).
A.?小李现在位置为第1排第2列????????????????????????????????B.?小张现在位置为第3排第2列
C.?小王现在位置为第2排第2列????????????????????????????????D.?小谢现在位置为第4排第2列
2.根据下列表述,能确定位置的是(?? )
A.?五一广场南区????????????B.?岳麓山北偏东42?????????????C.?学校致诚厅5排9座????????????D.?学校操场的西面
3.在平面直角坐标系中,点P(-1, 3)关于y轴对称点的坐标为(??? )
A.?(1,3)??????????????????????????????????B.?(-1,-3??????????????????????????????????C.?(-1,3)??????????????????????????????????D.?(1,-3)
4.已知点P(2a,1-3a)在第二象限,且点P到x轴的距离与到y轴的距离之和为6,则a的值为(??? )
A.?-1???????????????????????????????????????????B.?1???????????????????????????????????????????C.?5???????????????????????????????????????????D.?3
5.如图,? 的坐标为 若将线段 平移至 ,则a-b的值为( )?
A.?-1???????????????????????????????????????????B.?0???????????????????????????????????????????C.?1???????????????????????????????????????????D.?2
6.已知 ,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是(??? )
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
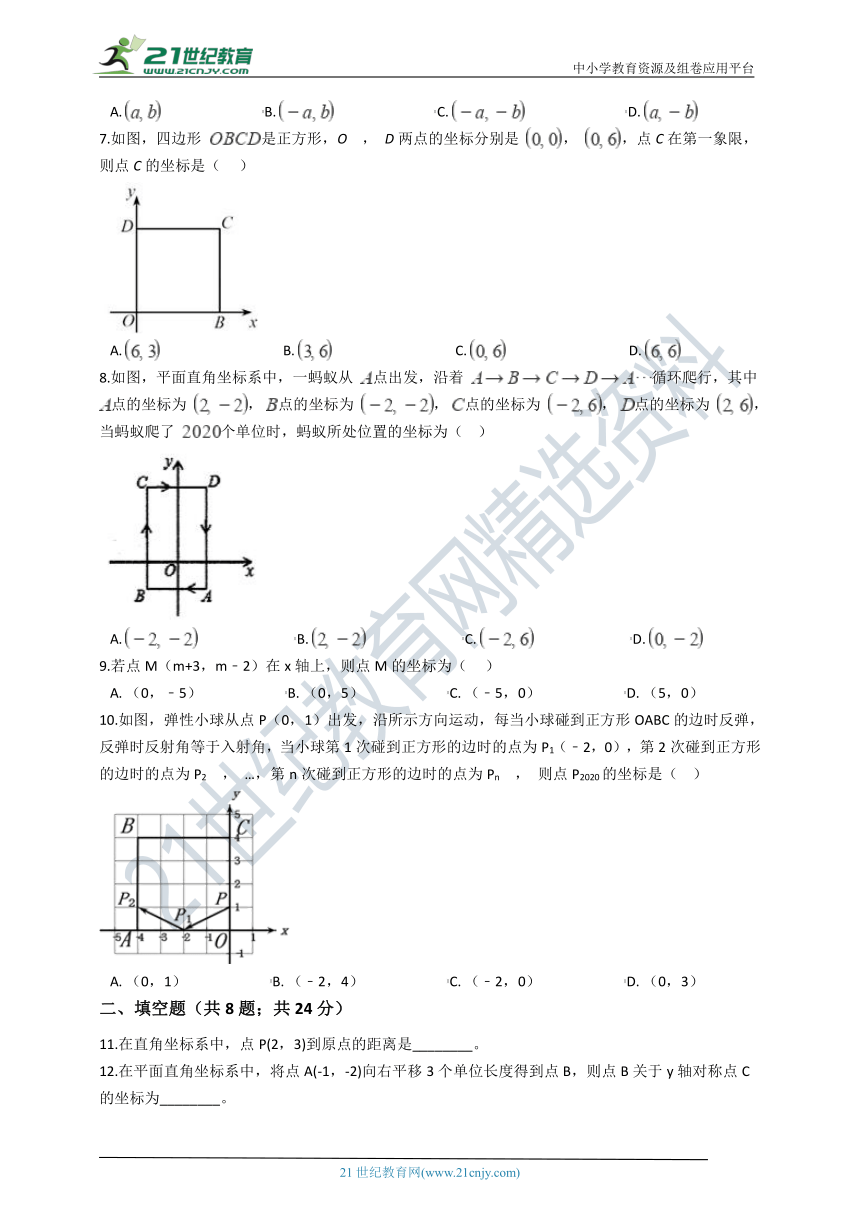
7.如图,四边形 是正方形,O , D两点的坐标分别是 , ,点C在第一象限,则点C的坐标是(??? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
8.如图,平面直角坐标系中,一蚂蚁从 点出发,沿着 循环爬行,其中 点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 ,当蚂蚁爬了 个单位时,蚂蚁所处位置的坐标为(?? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
9.若点M(m+3,m﹣2)在x轴上,则点M的坐标为(??? )
A.?(0,﹣5)????????????????????????B.?(0,5)????????????????????????C.?(﹣5,0)????????????????????????D.?(5,0)
10.如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为P1(﹣2,0),第2次碰到正方形的边时的点为P2 , …,第n次碰到正方形的边时的点为Pn , 则点P2020的坐标是(?? )
A.?(0,1)????????????????????????B.?(﹣2,4)????????????????????????C.?(﹣2,0)????????????????????????D.?(0,3)
二、填空题(共8题;共24分)
11.在直角坐标系中,点P(2,3)到原点的距离是________。
12.在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度得到点B,则点B关于y轴对称点C的坐标为________。
13.以水平数轴的原点 为圆心过正半轴 上的每一刻度点画同心圆,将 逆时针依次旋转 、 、 、 、 得到 条射线,构成如图所示的“圆”坐标系,点 、 的坐标分别表示为 、 ,则点 的坐标表示为________.
14.如图,在平面直角坐标系中, 的顶点A,B的坐标分别为 , ,把 沿x轴向右平移得到 ,如果点D的坐标为 ,则点E的坐标为________.
15.在平面直角坐标系中,已知点 和点 ,且直线 与坐标轴围成的三角形的面积等于 ,则 的值是________.
16.如果点 在第二象限,那么关于 的不等式 的解集是________.
17.北京市为了全民健身,举办“健步走”活动,活动场地位于奥林匹克公园(路线:森林公园→玲珑塔→国家体育馆→水立方)。如果体育局的工作人员在奥林匹克公园设计图上标记玲珑塔的坐标为 (-1,0) ,森林公园的坐标为 (-2,3) ,则终点水立方的坐标是________.
18.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“ ”方向排列,如(1,0),? (2,0),(2,1),(3,2),(3,1),(3,0)…根据这个规律探究可得,第115个点的坐标为________.
三、解答题(共6题;共46分)
19.在直角坐标系中,用线段顺次连结点(-2,0),(0,3),(3,3),
(0,4),(-2,0)。
(1)这是一个什么图形?
(2)求出它的面积;
20.写出如图中△ABC各顶点的坐标且求出此三角形的面积.
21.阅读与理解:
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右)爬行记为“+”,向下(或向左)爬行记为“-”,并且第一个数表示左右方向,第二个数表示上下方向。
例如:从A到B记为:A→B(+1,+4),
从D到C记为:D→C(-1,+2)。
思考与应用:
(1)图中A→C(________,________);
B→C(________,________);
D→A(________,________)。
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,-2),请在图中标出P的位置。
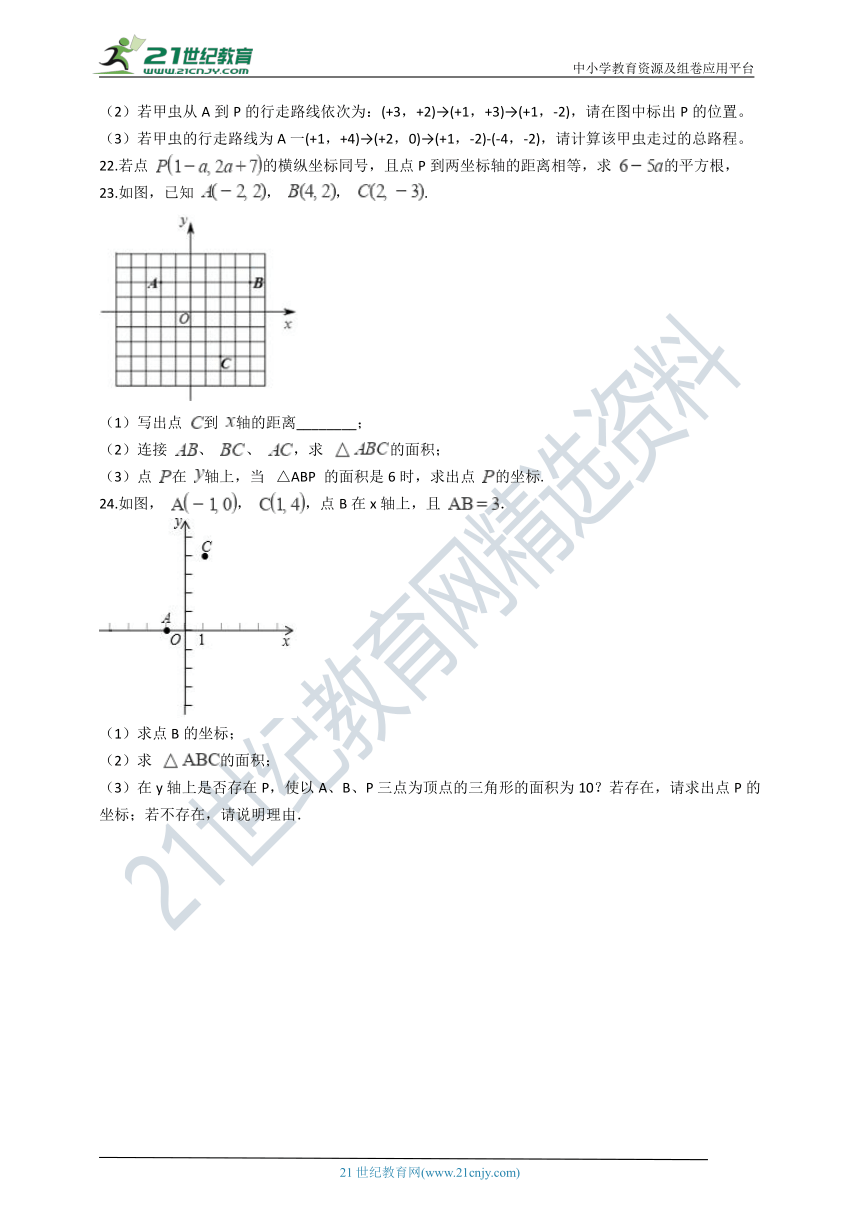
(3)若甲虫的行走路线为A一(+1,+4)→(+2,0)→(+1,-2)-(-4,-2),请计算该甲虫走过的总路程。
22.若点 的横纵坐标同号,且点P到两坐标轴的距离相等,求 的平方根,
23.如图,已知 , , .
(1)写出点 到 轴的距离________;
(2)连接 、 、 ,求 的面积;
(3)点 在 轴上,当? △ABP 的面积是6时,求出点 的坐标.
24.如图, , ,点B在x轴上,且 .
(1)求点B的坐标;
(2)求 的面积;
(3)在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
答案
一、选择题
1.解:A. 小李现在位置为第1排第4列,故A选项错误;
B. 小张现在位置为第3排第2列,故B选项正确;
C. 小王现在位置为第2排第3列,故C选项错误;
D. 小谢现在位置为第4排第4列,故D选项错误.
故答案为:B.
2.解:A、五一广场南区,不能确定位置,故本选项错误;
B、岳麓山北偏东42°,没有明确具体位置,故本选项错误;
C、学校致诚厅5排9座,能确定位置,故本选项正确;
D、学校操场的西面,不能确定位置,故本选项错误;
故答案为:C.
3.∵关于y轴对称的点,纵坐标相同,横坐标互为相反数,
∴点 关于y轴的对称点的坐标为 ,
故答案为:A.
4.∵点P(2a,1-3a)在第二象限,
∴2a<0,1-3a>0,
∴a<0,a< ,
∴a<0,
∵点P到x轴的距离与到y轴的距离之和为6,
∴|2a|+|1-3a|=6,
-2a+1-3a=6,
a=-1,
故答案为:A.
5.解:根据A(1,0)、B(0,2)、A1(3,b)、B1(a,4)可得
线段向右平移2个单位长度,向上平移两个单位长度,
则a=0+2=2,b=0+2=2,
所以a-b=2-2=0.
故答案为:B.
6.∵
∴
A: 在第一象限
B: 在第二象限
C: 在第三象限
D: 在第四象限
小手盖住的点位于第二象限
故答案为:B
7.解:∵O , D两点的坐标分别是 , ,
∴OD=6,
∵四边形 是正方形,
∴OB⊥BC , OB=BC=6
∴C点的坐标为: ,
故答案为:D .
8.解:∵A点坐标为(2,﹣2),B点坐标为(﹣2,﹣2),C点坐标为(﹣2,6),
∴AB=2﹣(﹣2)=4,BC=6﹣(﹣2)=8,
∴从A→B→C→D→A一圈的长度为2(AB+BC)=24.
∵2020=84×24+4,
∴当蚂蚁爬了2020个单位时,它所处位置在点A左边4个单位长度处,即(-2,﹣2).
故答案为:A
9.解:∵M(m+3,m﹣2)是x轴上的点,
∴m﹣2=0,
解得:m=2.
∴点M的坐标为(5,0).
故答案为:D.
10.解:如图,
根据反射角等于入射角画图,可知光线从P2反射后到P3(0,3),再反射到P4(-2,4),再反射到P5(-4,3),再反射到P点(0,1)之后,再循环反射,每6次一循环,2020÷6=336……4,即点P2020的坐标是(-2,4),
故答案为:B.
二、填空题
11.解:∵点P(2,3)到x轴的距离为3,到y轴的距离为2,
∴ 点P(2,3)到原点的距离=.
故答案为:.
12.解:将点A(-1,-2)向右平移3个单位长度得到点B,
∴B(-1+3,-2),即(2,-2),
点B关于y轴对称点C的坐标为:(-2,-2).
故答案为:(-2,-2).
13.解:图中为5个同心圆,且每条射线与x轴所形成的角度已知, 、 的坐标分别表示为 、 ,根据点的特征,所以点 的坐标表示为 ;
故答案为: .
14.解:由题意知:A、B两点之间的横坐标差为: ,
由平移性质可知:E、D两点横坐标之差与B、A两点横坐标之差相等,
设E点横坐标为a,
则a-6=1,∴a=7,
∴E点坐标为(7,0) .
故答案为:(7,0) .
15.解:∵点A的坐标为(a,0),点B的坐标为(0,4),
∴OA=|a|,OB=4.
又∵S△OAB=12,
∴ ×4×|a|=12,
解得:a= .
故答案为: .
16.∵点 在第二象限,
∴ ,
解得 ,
∴ .
∵ ,
∴ ,
故答案为: .
17.解:根据玲珑塔的坐标可知,原点的坐标位置
∴水立方的坐标为(-2,-3)
18.解:∵横坐标为1的点只有1个,纵坐标为0;
横坐标为2的点有2个,纵坐标分别为0,1;
横坐标为3的点有3个,纵坐标分别为0,1,2
横坐标为4的点有4个,纵坐标分别为0,1,2,3
偶数行箭头向上,奇数行箭头向下;
1+2+3++14=105.
∵偶数列箭头向上,第105个点的坐标为(14,13)
∵115-10=105
∵奇函数列的箭头向下,
∴第115个点的横坐标为15,纵坐标为14-10+1=5‘’
∴第115个点为:(15,5).
故答案为:(15,5).
三、解答题
19.解:(1)如图所示:得到一个四边形;
(2)面积=1/2×1×2+1/2×1×3=2.5;
20. 解:根据图形得:A(2,2)、B(-2,-1)、C(3,-2),
三角形的面积是 =5×4-6-2-2.5=9.5.
故答案为:A(2,2)、B(-2,-1)、C(3,-2),三角形的面积是9.5.
21. (1)+3;+4;+2;0;﹣4;﹣2
(2)解:如图2所示.
(3)解:甲虫走过的总路程:
|+1|+|+4|+|+2|+|+1|+|﹣2|+|﹣4|+|﹣2|=16.
22. 解:由题意,得 ,解得 ,
故 ,
的平方根为
23. (1)3
(2)解:如图,
(3)解:设点P的坐标为(0,b),
则点P到AB的距离为 ,AB=6
S△ABP= =6解得b=0或b=4
∴点P的坐标为(0,0)或(0,4)
解:(1)∵C(2,-3),
∴点C到x轴的距离是3,
故答案为:3.
24. (1)解:当点B在点A的右边时,点B的坐标为(2,0);
当点B在点A的左边时,点B的坐标为(-4,0).
所以点B的坐标为(2,0)或(-4,0)
(2)解:三角形ABC的面积为 ×3×4=6.
(3)解:设点P到x轴的距离为h,则
×3h=10,解得h= .
①当点P在y轴正半轴时,点P的坐标为(0, );
②当点P在y轴负半轴时,点P的坐标为(0,- ).
综上所述,点P的坐标为(0, )或(0,- )
_21?????????è?????(www.21cnjy.com)_
2020年苏科版八年级数学上册第五章 平面直角坐标系单元测试卷解析版
一、选择题(共10题;共30分)
1.小李、小王、小张、小谢原有位置如图(横为排、竖为列),小李在第2排第4列,小王在第3排第3列,小张在第4排第2列,小谢在第5排第4列.撤走第一排,仍按照原有确定位置的方法确定新的位置,下列说法正确的是(?? ).
A.?小李现在位置为第1排第2列????????????????????????????????B.?小张现在位置为第3排第2列
C.?小王现在位置为第2排第2列????????????????????????????????D.?小谢现在位置为第4排第2列
2.根据下列表述,能确定位置的是(?? )
A.?五一广场南区????????????B.?岳麓山北偏东42?????????????C.?学校致诚厅5排9座????????????D.?学校操场的西面
3.在平面直角坐标系中,点P(-1, 3)关于y轴对称点的坐标为(??? )
A.?(1,3)??????????????????????????????????B.?(-1,-3??????????????????????????????????C.?(-1,3)??????????????????????????????????D.?(1,-3)
4.已知点P(2a,1-3a)在第二象限,且点P到x轴的距离与到y轴的距离之和为6,则a的值为(??? )
A.?-1???????????????????????????????????????????B.?1???????????????????????????????????????????C.?5???????????????????????????????????????????D.?3
5.如图,? 的坐标为 若将线段 平移至 ,则a-b的值为( )?
A.?-1???????????????????????????????????????????B.?0???????????????????????????????????????????C.?1???????????????????????????????????????????D.?2
6.已知 ,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是(??? )
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
7.如图,四边形 是正方形,O , D两点的坐标分别是 , ,点C在第一象限,则点C的坐标是(??? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
8.如图,平面直角坐标系中,一蚂蚁从 点出发,沿着 循环爬行,其中 点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 ,当蚂蚁爬了 个单位时,蚂蚁所处位置的坐标为(?? )
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
9.若点M(m+3,m﹣2)在x轴上,则点M的坐标为(??? )
A.?(0,﹣5)????????????????????????B.?(0,5)????????????????????????C.?(﹣5,0)????????????????????????D.?(5,0)
10.如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为P1(﹣2,0),第2次碰到正方形的边时的点为P2 , …,第n次碰到正方形的边时的点为Pn , 则点P2020的坐标是(?? )
A.?(0,1)????????????????????????B.?(﹣2,4)????????????????????????C.?(﹣2,0)????????????????????????D.?(0,3)
二、填空题(共8题;共24分)
11.在直角坐标系中,点P(2,3)到原点的距离是________。
12.在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度得到点B,则点B关于y轴对称点C的坐标为________。
13.以水平数轴的原点 为圆心过正半轴 上的每一刻度点画同心圆,将 逆时针依次旋转 、 、 、 、 得到 条射线,构成如图所示的“圆”坐标系,点 、 的坐标分别表示为 、 ,则点 的坐标表示为________.
14.如图,在平面直角坐标系中, 的顶点A,B的坐标分别为 , ,把 沿x轴向右平移得到 ,如果点D的坐标为 ,则点E的坐标为________.
15.在平面直角坐标系中,已知点 和点 ,且直线 与坐标轴围成的三角形的面积等于 ,则 的值是________.
16.如果点 在第二象限,那么关于 的不等式 的解集是________.
17.北京市为了全民健身,举办“健步走”活动,活动场地位于奥林匹克公园(路线:森林公园→玲珑塔→国家体育馆→水立方)。如果体育局的工作人员在奥林匹克公园设计图上标记玲珑塔的坐标为 (-1,0) ,森林公园的坐标为 (-2,3) ,则终点水立方的坐标是________.
18.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“ ”方向排列,如(1,0),? (2,0),(2,1),(3,2),(3,1),(3,0)…根据这个规律探究可得,第115个点的坐标为________.
三、解答题(共6题;共46分)
19.在直角坐标系中,用线段顺次连结点(-2,0),(0,3),(3,3),
(0,4),(-2,0)。
(1)这是一个什么图形?
(2)求出它的面积;
20.写出如图中△ABC各顶点的坐标且求出此三角形的面积.
21.阅读与理解:
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右)爬行记为“+”,向下(或向左)爬行记为“-”,并且第一个数表示左右方向,第二个数表示上下方向。
例如:从A到B记为:A→B(+1,+4),
从D到C记为:D→C(-1,+2)。
思考与应用:
(1)图中A→C(________,________);
B→C(________,________);
D→A(________,________)。
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,-2),请在图中标出P的位置。
(3)若甲虫的行走路线为A一(+1,+4)→(+2,0)→(+1,-2)-(-4,-2),请计算该甲虫走过的总路程。
22.若点 的横纵坐标同号,且点P到两坐标轴的距离相等,求 的平方根,
23.如图,已知 , , .
(1)写出点 到 轴的距离________;
(2)连接 、 、 ,求 的面积;
(3)点 在 轴上,当? △ABP 的面积是6时,求出点 的坐标.
24.如图, , ,点B在x轴上,且 .
(1)求点B的坐标;
(2)求 的面积;
(3)在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
答案
一、选择题
1.解:A. 小李现在位置为第1排第4列,故A选项错误;
B. 小张现在位置为第3排第2列,故B选项正确;
C. 小王现在位置为第2排第3列,故C选项错误;
D. 小谢现在位置为第4排第4列,故D选项错误.
故答案为:B.
2.解:A、五一广场南区,不能确定位置,故本选项错误;
B、岳麓山北偏东42°,没有明确具体位置,故本选项错误;
C、学校致诚厅5排9座,能确定位置,故本选项正确;
D、学校操场的西面,不能确定位置,故本选项错误;
故答案为:C.
3.∵关于y轴对称的点,纵坐标相同,横坐标互为相反数,
∴点 关于y轴的对称点的坐标为 ,
故答案为:A.
4.∵点P(2a,1-3a)在第二象限,
∴2a<0,1-3a>0,
∴a<0,a< ,
∴a<0,
∵点P到x轴的距离与到y轴的距离之和为6,
∴|2a|+|1-3a|=6,
-2a+1-3a=6,
a=-1,
故答案为:A.
5.解:根据A(1,0)、B(0,2)、A1(3,b)、B1(a,4)可得
线段向右平移2个单位长度,向上平移两个单位长度,
则a=0+2=2,b=0+2=2,
所以a-b=2-2=0.
故答案为:B.
6.∵
∴
A: 在第一象限
B: 在第二象限
C: 在第三象限
D: 在第四象限
小手盖住的点位于第二象限
故答案为:B
7.解:∵O , D两点的坐标分别是 , ,
∴OD=6,
∵四边形 是正方形,
∴OB⊥BC , OB=BC=6
∴C点的坐标为: ,
故答案为:D .
8.解:∵A点坐标为(2,﹣2),B点坐标为(﹣2,﹣2),C点坐标为(﹣2,6),
∴AB=2﹣(﹣2)=4,BC=6﹣(﹣2)=8,
∴从A→B→C→D→A一圈的长度为2(AB+BC)=24.
∵2020=84×24+4,
∴当蚂蚁爬了2020个单位时,它所处位置在点A左边4个单位长度处,即(-2,﹣2).
故答案为:A
9.解:∵M(m+3,m﹣2)是x轴上的点,
∴m﹣2=0,
解得:m=2.
∴点M的坐标为(5,0).
故答案为:D.
10.解:如图,
根据反射角等于入射角画图,可知光线从P2反射后到P3(0,3),再反射到P4(-2,4),再反射到P5(-4,3),再反射到P点(0,1)之后,再循环反射,每6次一循环,2020÷6=336……4,即点P2020的坐标是(-2,4),
故答案为:B.
二、填空题
11.解:∵点P(2,3)到x轴的距离为3,到y轴的距离为2,
∴ 点P(2,3)到原点的距离=.
故答案为:.
12.解:将点A(-1,-2)向右平移3个单位长度得到点B,
∴B(-1+3,-2),即(2,-2),
点B关于y轴对称点C的坐标为:(-2,-2).
故答案为:(-2,-2).
13.解:图中为5个同心圆,且每条射线与x轴所形成的角度已知, 、 的坐标分别表示为 、 ,根据点的特征,所以点 的坐标表示为 ;
故答案为: .
14.解:由题意知:A、B两点之间的横坐标差为: ,
由平移性质可知:E、D两点横坐标之差与B、A两点横坐标之差相等,
设E点横坐标为a,
则a-6=1,∴a=7,
∴E点坐标为(7,0) .
故答案为:(7,0) .
15.解:∵点A的坐标为(a,0),点B的坐标为(0,4),
∴OA=|a|,OB=4.
又∵S△OAB=12,
∴ ×4×|a|=12,
解得:a= .
故答案为: .
16.∵点 在第二象限,
∴ ,
解得 ,
∴ .
∵ ,
∴ ,
故答案为: .
17.解:根据玲珑塔的坐标可知,原点的坐标位置
∴水立方的坐标为(-2,-3)
18.解:∵横坐标为1的点只有1个,纵坐标为0;
横坐标为2的点有2个,纵坐标分别为0,1;
横坐标为3的点有3个,纵坐标分别为0,1,2
横坐标为4的点有4个,纵坐标分别为0,1,2,3
偶数行箭头向上,奇数行箭头向下;
1+2+3++14=105.
∵偶数列箭头向上,第105个点的坐标为(14,13)
∵115-10=105
∵奇函数列的箭头向下,
∴第115个点的横坐标为15,纵坐标为14-10+1=5‘’
∴第115个点为:(15,5).
故答案为:(15,5).
三、解答题
19.解:(1)如图所示:得到一个四边形;
(2)面积=1/2×1×2+1/2×1×3=2.5;
20. 解:根据图形得:A(2,2)、B(-2,-1)、C(3,-2),
三角形的面积是 =5×4-6-2-2.5=9.5.
故答案为:A(2,2)、B(-2,-1)、C(3,-2),三角形的面积是9.5.
21. (1)+3;+4;+2;0;﹣4;﹣2
(2)解:如图2所示.
(3)解:甲虫走过的总路程:
|+1|+|+4|+|+2|+|+1|+|﹣2|+|﹣4|+|﹣2|=16.
22. 解:由题意,得 ,解得 ,
故 ,
的平方根为
23. (1)3
(2)解:如图,
(3)解:设点P的坐标为(0,b),
则点P到AB的距离为 ,AB=6
S△ABP= =6解得b=0或b=4
∴点P的坐标为(0,0)或(0,4)
解:(1)∵C(2,-3),
∴点C到x轴的距离是3,
故答案为:3.
24. (1)解:当点B在点A的右边时,点B的坐标为(2,0);
当点B在点A的左边时,点B的坐标为(-4,0).
所以点B的坐标为(2,0)或(-4,0)
(2)解:三角形ABC的面积为 ×3×4=6.
(3)解:设点P到x轴的距离为h,则
×3h=10,解得h= .
①当点P在y轴正半轴时,点P的坐标为(0, );
②当点P在y轴负半轴时,点P的坐标为(0,- ).
综上所述,点P的坐标为(0, )或(0,- )
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
