2020-2021学年华东师大新版七年级上册数学《第5章 相交线与平行线》单元测试题(Word版 含解析)
文档属性
| 名称 | 2020-2021学年华东师大新版七年级上册数学《第5章 相交线与平行线》单元测试题(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 189.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 19:45:47 | ||
图片预览


文档简介
2020-2021学年华东师大新版七年级上册数学《第5章
相交线与平行线》单元测试题
一.选择题(共10小题)
1.下列四个图形中,∠1和∠2是对顶角的图形有( )
A.1个
B.2个
C.3个
D.4个
2.如图所示,AC⊥BC,AD⊥CD,AB=m,CD=n,则AC的取值范围是( )
A.大于n
B.小于m
C.大于n小于m
D.无法确定
3.如图,与∠α是同位角的有( )个.
A.3个
B.4个
C.5个
D.6个
4.下列说法中,正确的是( )
A.不相交的两条直线是平行线
B.过一点有且只有一条直线与已知直线平行
C.从直线外一点作这条直线的垂线段叫做点到这条直线的距离
D.在同一平面内,一条直线与两条平行线中的一条垂直,则与另一条也垂直
5.如图,若AO⊥CO,BO⊥DO,且∠BOC=a,则∠AOD等于( )
A.180°﹣2a
B.180°﹣a
C.90°+a
D.2a﹣90°
6.直线MN外有一点P,如果点P到MN的距离为3,Q是直线MN上的任意一点,那么线段PQ的长度应满足关系( )
A.PQ≥3
B.PQ>3
C.PQ=3
D.PQ<3
7.如图,下列说法正确的是( )
A.∠1和∠B是同旁内角
B.∠1和∠C是内错角
C.∠2和∠B是同位角
D.∠3和∠C同旁内角
8.如图是一个安全用电标记图案,可以抽象为右边的几何图形,其中AB∥DC,BE∥FC.点E,F在AD上,若∠A=16°,∠B=66°,则∠AFC的度数是( )
A.50°
B.66°
C.82°
D.89°
9.如图,下列推理正确的是( )
A.∵∠1=∠2,∴AB∥CD
B.∵∠1+∠2=180°,∴AB∥CD
C.∵∠3=∠4,∴AB∥CD
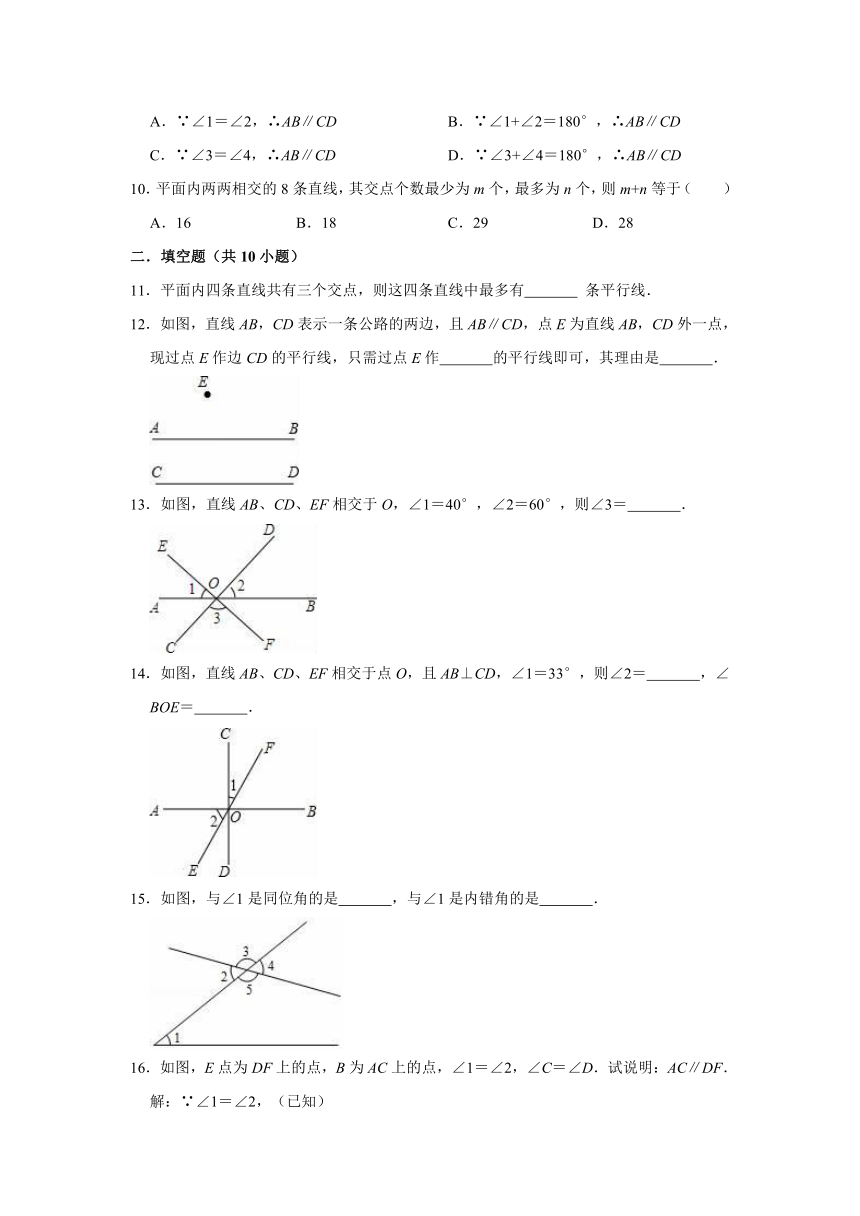
D.∵∠3+∠4=180°,∴AB∥CD
10.平面内两两相交的8条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.16
B.18
C.29
D.28
二.填空题(共10小题)
11.平面内四条直线共有三个交点,则这四条直线中最多有
条平行线.
12.如图,直线AB,CD表示一条公路的两边,且AB∥CD,点E为直线AB,CD外一点,现过点E作边CD的平行线,只需过点E作
的平行线即可,其理由是
.
13.如图,直线AB、CD、EF相交于O,∠1=40°,∠2=60°,则∠3=
.
14.如图,直线AB、CD、EF相交于点O,且AB⊥CD,∠1=33°,则∠2=
,∠BOE=
.
15.如图,与∠1是同位角的是
,与∠1是内错角的是
.
16.如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
解:∵∠1=∠2,(已知)
∠1=∠3,(
)
∴∠2=∠3,(等量代换)
∴
∥
,(
)
∴∠C=∠ABD,(
)
又∵∠C=∠D,(已知)
∴∠D=∠ABD,(
)
∴AC∥DF.(
)
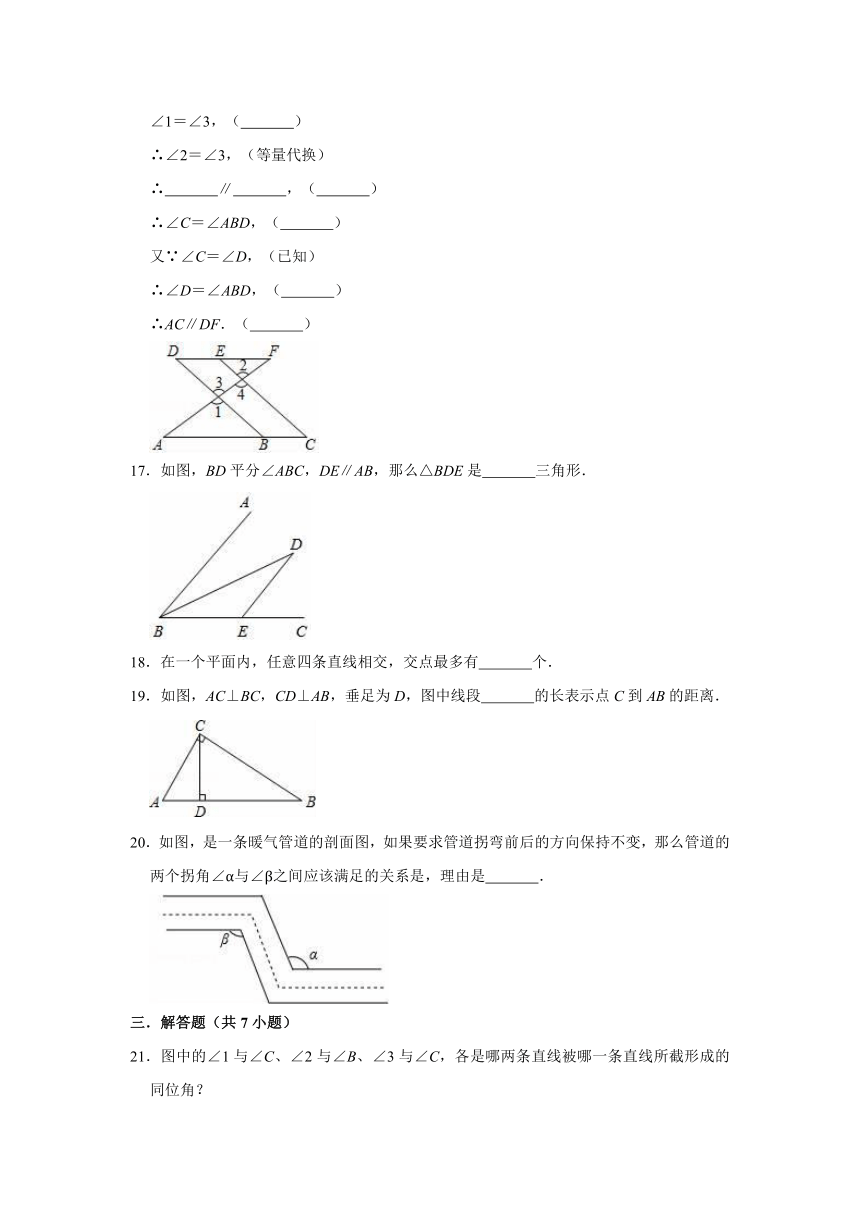
17.如图,BD平分∠ABC,DE∥AB,那么△BDE是
三角形.
18.在一个平面内,任意四条直线相交,交点最多有
个.
19.如图,AC⊥BC,CD⊥AB,垂足为D,图中线段
的长表示点C到AB的距离.
20.如图,是一条暖气管道的剖面图,如果要求管道拐弯前后的方向保持不变,那么管道的两个拐角∠α与∠β之间应该满足的关系是,理由是
.
三.解答题(共7小题)
21.图中的∠1与∠C、∠2与∠B、∠3与∠C,各是哪两条直线被哪一条直线所截形成的同位角?
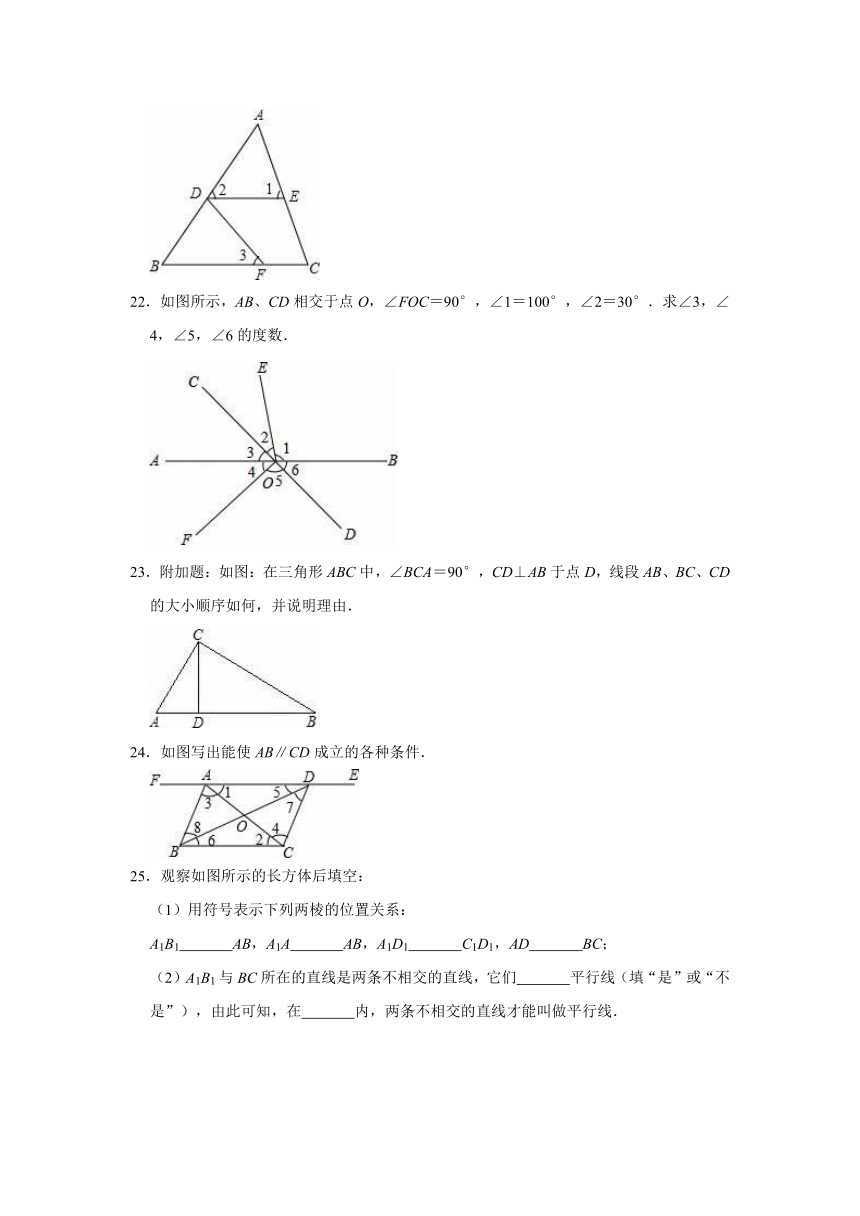
22.如图所示,AB、CD相交于点O,∠FOC=90°,∠1=100°,∠2=30°.求∠3,∠4,∠5,∠6的度数.
23.附加题:如图:在三角形ABC中,∠BCA=90°,CD⊥AB于点D,线段AB、BC、CD的大小顺序如何,并说明理由.
24.如图写出能使AB∥CD成立的各种条件.
25.观察如图所示的长方体后填空:
(1)用符号表示下列两棱的位置关系:
A1B1
AB,A1A
AB,A1D1
C1D1,AD
BC;
(2)A1B1与BC所在的直线是两条不相交的直线,它们
平行线(填“是”或“不是”),由此可知,在
内,两条不相交的直线才能叫做平行线.
26.平面上有9条直线,任意两条都不平行,欲使它们出现29个交点,能否做到,如果能,怎么安排才能做到?如果不能,请说明理由.
27.如图,已知AB∥CD,BE平分∠ABC.BE垂直于CE,求证:CE平分∠BCD.
参考答案与试题解析
一.选择题(共10小题)
1.解:图①,∠1和∠2不是对顶角,
图②,∠1和∠2是对顶角,
图③,∠1和∠2是对顶角,
图④,∠1和∠2是对顶角,
综上所述,∠1和∠2是对顶角有3个.
故选:C.
2.解:∵AC⊥BC,
∴AC<AB,
∵AD⊥CD,
∴AC>CD,
∴CD<AC<AB,
∵AB=m,CD=n,
∴AC的取值范围是:大于n小于m.
故选:C.
3.解:此题中构成∠α的两线m、y都可作为截线,
①以y为截线,∠α有1个同位角,
②以m为截线,∠α有2个同位角.
因此共有3个∠α的同位角.
故选:A.
4.解:A、不相交的两条直线是平行线,要在同一平面内的前提条件下,故A选项错误;
B、过一点有且只有一条直线与已知直线平行,过直线外一点,故B选项错误;
C、从直线外一点作这条直线的垂线段叫做点到这条直线的距离,应为垂线段的长度,故C选项错误;
D、在同一平面内,一条直线与两条平行线中的一条垂直,则与另一条也垂直,故D选项正确.
故选:D.
5.解:∵AO⊥CO,BO⊥DO,
∴∠BOD=∠AOC=90°,
∵∠BOC=α,
∴∠DOC=α﹣90°,
∴∠AOD=90°﹣∠DOC=90°﹣(α﹣90°)
=180°﹣α.
故选:B.
6.解:∵点P到MN的距离为3,Q是直线MN上的任意一点,
∴PQ≥3,
故选:A.
7.解:A、∠1和∠B是同位角,故本选项错误;
B、∠1和∠C既不是同位角、内错角,也不是同旁内角,故本选项错误;
C、∠2和∠B既不是同位角、内错角,也不是同旁内角,故本选项错误;
D、∠3和∠C是同旁内角,故本选项正确.
故选:D.
8.解:在△ABE中,∵∠A=16°,∠B=66°,
∴∠BEA=98°.
∵BE∥FC,
∴∠CFE=∠BEA=98°,
∴∠AFC=82°.
故选:C.
9.解:∵∠1+∠2=180°,∴AB∥CD,故A选项错误;
∵∠1+∠2=180°,∴AB∥CD,故B选项正确;
∵∠3=∠4,∴EF∥GH,故C选项错误;
∠3+∠4=180°不能判定AB∥CD,故D选项错误.
故选:B.
10.解:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,
∵任意三条直线不过同一点,
∴此时交点为:8×(8﹣1)÷2=28,即n=28;
则m+n=29.
故选:C.
二.填空题(共10小题)
11.解:若四条直线相互平行,则没有交点;
若四条直线中有三条直线相互平行,则此时恰好有三个交点;
若四条直线中有两条直线相互平行,另两条不平行,则此时有三个交点或五个交点;
若四条直线中有两条直线相互平行,另两条也平行,但它们之间相互不平行,则此时有四个交点;
若四条直线中没有平行线,则此时的交点是一个或四个或六个.
综上可知,平面内四条直线共有三个交点,则这四条直线中最多有三条平行线.
故答案是:三.
12.解:只需过点E作AB的平行线即可,其理由是平行于同一直线的两直线互相平行.
故答案为:AB,平行于同一直线的两直线互相平行.
13.解:从图上可以知道∠1+∠2+∠3=180°,
∵∠1=40°,∠2=60°,
∴∠3=80°,
故答案为:80°
14.解:∵∠EOD与∠1互为对顶角,
∴∠EOD=∠1=33°,
又∵AB⊥CD,
∴∠AOD=∠BOD=90°,
∴∠2=90°﹣∠EOD=57°,∠BOE=90°+∠EOD=123°.
故答案为:57°,123°.
15.解:与∠1是同位角的是∠4,与∠1是内错角的是∠2,
故答案为:∠4;∠2.
16.解:∵∠1=∠2(已知),
∠1=∠3(对顶角相等),
∴∠2=∠3(等量代换),
∴EC∥DB(同位角相等,两直线平行),
∴∠C=∠ABD
(两直线平行,同位角相等),
又∵∠C=∠D(已知),
∴∠D=∠ABD(等量代换),
∴AC∥DF(内错角相等,两直线平行).
故答案为:对顶角相等;BD;CE;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行.
17.解:∵BD平分∠ABC,
∴∠ABD=∠EBD,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠BDE=∠EBD,
∴BE=DE,
∴△BDE是等腰三角形三角形.
故答案为:等腰.
18.解:如图所示:
①当4条直线经过同一个点时,
有1个交点;
②当3条直线经过同一个点,第4条不经过该点时,
有4个交点;
③当4条直线不经过同一点时,
有6个交点.
综上所述,4条直线相交最多有6个交点.
故答案为:6.
19.解:∵CD⊥AB,
∴线段CD的长度表示点C到AB的距离.
故答案为;CD.
20.解:∵管道拐弯前后的方向保持不变,
∴管道的两个拐角∠α=∠β.
故答案为:内错角相等,两直线平行.
三.解答题(共7小题)
21.解:如图,∠1与∠C是直线DE、BC被直线AC所截形成的同位角,∠2与∠B是直线DE、BC被直线AB所截形成的同位角,∠3与∠C是直线DF、
AC被直线BC所截形成的同位角.
22.解:如图,∵∠1+∠2+∠3=180°,∠1=100°,∠2=30°,
∴∠3=50°,
∴∠6=∠3=50°.
又∵∠FOC=90°,
∴∠3+∠4=90°,
∴∠4=40°.
∵∠FOC+∠5=180°,
∴∠5=90°.
综上所述,∠3,∠4,∠5,∠6的度数分别是:50°、40°、90°、50°.
23.解:∵CD⊥AB于点D,
∴BC>CD;
∵∠BCA=90°,
∴AB>BC;
∴AB>BC>CD.
24.解:AB∥CD的条件为∠7=∠8或∠3=∠4或∠BAD+∠ADC=180°或∠ABC+∠BCD=180°或∠FAB=∠FDC或∠EDC=∠EAB.
25.解:(1)如图,在矩形ABB1A1中,A1B1∥AB,A1A⊥AB;
在矩形A1B1C1D1中,A1D1⊥C1D1;
在矩形ABCD中,AD∥BC.
故答案分别是:∥,⊥,⊥,∥;
(2)根据图示知,直线A1B1与BC不在同一平面内,所以它们虽然没有交点,但是它们也不平行.
故答案是:不是,同一平面.
26.解:能.理由如下:
9条直线,任意两条都不平行,最多交点的个数是==36,
∵36>29,
∴能出现29个交点,
安排如下:先使4条直线相交于一点P,另外5条直线两两相交最多可得=10个交点,
与前四条直线相交最多可得5×4=20个交点,
让其中两个点重合为点O,所以交点减少1个,
交点个数一共有10+20﹣1=29个.
故能做到.
27.证明:过E作EF∥AB
交BC于点F,
∴∠ABE=∠FEB,
∵AB∥CD,
∴EF∥CD,∠ABC+∠BCD=180°,
∴∠DCE=∠FEC,
∵BE⊥CE,
∴∠BEF+∠CEF=∠ABE+∠DCE=90°,
∴∠EBC+∠ECB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠DCE=∠BCE,
∴CE平分∠BCD.
相交线与平行线》单元测试题
一.选择题(共10小题)
1.下列四个图形中,∠1和∠2是对顶角的图形有( )
A.1个
B.2个
C.3个
D.4个
2.如图所示,AC⊥BC,AD⊥CD,AB=m,CD=n,则AC的取值范围是( )
A.大于n
B.小于m
C.大于n小于m
D.无法确定
3.如图,与∠α是同位角的有( )个.
A.3个
B.4个
C.5个
D.6个
4.下列说法中,正确的是( )
A.不相交的两条直线是平行线
B.过一点有且只有一条直线与已知直线平行
C.从直线外一点作这条直线的垂线段叫做点到这条直线的距离
D.在同一平面内,一条直线与两条平行线中的一条垂直,则与另一条也垂直
5.如图,若AO⊥CO,BO⊥DO,且∠BOC=a,则∠AOD等于( )
A.180°﹣2a
B.180°﹣a
C.90°+a
D.2a﹣90°
6.直线MN外有一点P,如果点P到MN的距离为3,Q是直线MN上的任意一点,那么线段PQ的长度应满足关系( )
A.PQ≥3
B.PQ>3
C.PQ=3
D.PQ<3
7.如图,下列说法正确的是( )
A.∠1和∠B是同旁内角
B.∠1和∠C是内错角
C.∠2和∠B是同位角
D.∠3和∠C同旁内角
8.如图是一个安全用电标记图案,可以抽象为右边的几何图形,其中AB∥DC,BE∥FC.点E,F在AD上,若∠A=16°,∠B=66°,则∠AFC的度数是( )
A.50°
B.66°
C.82°
D.89°
9.如图,下列推理正确的是( )
A.∵∠1=∠2,∴AB∥CD
B.∵∠1+∠2=180°,∴AB∥CD
C.∵∠3=∠4,∴AB∥CD
D.∵∠3+∠4=180°,∴AB∥CD
10.平面内两两相交的8条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.16
B.18
C.29
D.28
二.填空题(共10小题)
11.平面内四条直线共有三个交点,则这四条直线中最多有
条平行线.
12.如图,直线AB,CD表示一条公路的两边,且AB∥CD,点E为直线AB,CD外一点,现过点E作边CD的平行线,只需过点E作
的平行线即可,其理由是
.
13.如图,直线AB、CD、EF相交于O,∠1=40°,∠2=60°,则∠3=
.
14.如图,直线AB、CD、EF相交于点O,且AB⊥CD,∠1=33°,则∠2=
,∠BOE=
.
15.如图,与∠1是同位角的是
,与∠1是内错角的是
.
16.如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
解:∵∠1=∠2,(已知)
∠1=∠3,(
)
∴∠2=∠3,(等量代换)
∴
∥
,(
)
∴∠C=∠ABD,(
)
又∵∠C=∠D,(已知)
∴∠D=∠ABD,(
)
∴AC∥DF.(
)
17.如图,BD平分∠ABC,DE∥AB,那么△BDE是
三角形.
18.在一个平面内,任意四条直线相交,交点最多有
个.
19.如图,AC⊥BC,CD⊥AB,垂足为D,图中线段
的长表示点C到AB的距离.
20.如图,是一条暖气管道的剖面图,如果要求管道拐弯前后的方向保持不变,那么管道的两个拐角∠α与∠β之间应该满足的关系是,理由是
.
三.解答题(共7小题)
21.图中的∠1与∠C、∠2与∠B、∠3与∠C,各是哪两条直线被哪一条直线所截形成的同位角?
22.如图所示,AB、CD相交于点O,∠FOC=90°,∠1=100°,∠2=30°.求∠3,∠4,∠5,∠6的度数.
23.附加题:如图:在三角形ABC中,∠BCA=90°,CD⊥AB于点D,线段AB、BC、CD的大小顺序如何,并说明理由.
24.如图写出能使AB∥CD成立的各种条件.
25.观察如图所示的长方体后填空:
(1)用符号表示下列两棱的位置关系:
A1B1
AB,A1A
AB,A1D1
C1D1,AD
BC;
(2)A1B1与BC所在的直线是两条不相交的直线,它们
平行线(填“是”或“不是”),由此可知,在
内,两条不相交的直线才能叫做平行线.
26.平面上有9条直线,任意两条都不平行,欲使它们出现29个交点,能否做到,如果能,怎么安排才能做到?如果不能,请说明理由.
27.如图,已知AB∥CD,BE平分∠ABC.BE垂直于CE,求证:CE平分∠BCD.
参考答案与试题解析
一.选择题(共10小题)
1.解:图①,∠1和∠2不是对顶角,
图②,∠1和∠2是对顶角,
图③,∠1和∠2是对顶角,
图④,∠1和∠2是对顶角,
综上所述,∠1和∠2是对顶角有3个.
故选:C.
2.解:∵AC⊥BC,
∴AC<AB,
∵AD⊥CD,
∴AC>CD,
∴CD<AC<AB,
∵AB=m,CD=n,
∴AC的取值范围是:大于n小于m.
故选:C.
3.解:此题中构成∠α的两线m、y都可作为截线,
①以y为截线,∠α有1个同位角,
②以m为截线,∠α有2个同位角.
因此共有3个∠α的同位角.
故选:A.
4.解:A、不相交的两条直线是平行线,要在同一平面内的前提条件下,故A选项错误;
B、过一点有且只有一条直线与已知直线平行,过直线外一点,故B选项错误;
C、从直线外一点作这条直线的垂线段叫做点到这条直线的距离,应为垂线段的长度,故C选项错误;
D、在同一平面内,一条直线与两条平行线中的一条垂直,则与另一条也垂直,故D选项正确.
故选:D.
5.解:∵AO⊥CO,BO⊥DO,
∴∠BOD=∠AOC=90°,
∵∠BOC=α,
∴∠DOC=α﹣90°,
∴∠AOD=90°﹣∠DOC=90°﹣(α﹣90°)
=180°﹣α.
故选:B.
6.解:∵点P到MN的距离为3,Q是直线MN上的任意一点,
∴PQ≥3,
故选:A.
7.解:A、∠1和∠B是同位角,故本选项错误;
B、∠1和∠C既不是同位角、内错角,也不是同旁内角,故本选项错误;
C、∠2和∠B既不是同位角、内错角,也不是同旁内角,故本选项错误;
D、∠3和∠C是同旁内角,故本选项正确.
故选:D.
8.解:在△ABE中,∵∠A=16°,∠B=66°,
∴∠BEA=98°.
∵BE∥FC,
∴∠CFE=∠BEA=98°,
∴∠AFC=82°.
故选:C.
9.解:∵∠1+∠2=180°,∴AB∥CD,故A选项错误;
∵∠1+∠2=180°,∴AB∥CD,故B选项正确;
∵∠3=∠4,∴EF∥GH,故C选项错误;
∠3+∠4=180°不能判定AB∥CD,故D选项错误.
故选:B.
10.解:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,
∵任意三条直线不过同一点,
∴此时交点为:8×(8﹣1)÷2=28,即n=28;
则m+n=29.
故选:C.
二.填空题(共10小题)
11.解:若四条直线相互平行,则没有交点;
若四条直线中有三条直线相互平行,则此时恰好有三个交点;
若四条直线中有两条直线相互平行,另两条不平行,则此时有三个交点或五个交点;
若四条直线中有两条直线相互平行,另两条也平行,但它们之间相互不平行,则此时有四个交点;
若四条直线中没有平行线,则此时的交点是一个或四个或六个.
综上可知,平面内四条直线共有三个交点,则这四条直线中最多有三条平行线.
故答案是:三.
12.解:只需过点E作AB的平行线即可,其理由是平行于同一直线的两直线互相平行.
故答案为:AB,平行于同一直线的两直线互相平行.
13.解:从图上可以知道∠1+∠2+∠3=180°,
∵∠1=40°,∠2=60°,
∴∠3=80°,
故答案为:80°
14.解:∵∠EOD与∠1互为对顶角,
∴∠EOD=∠1=33°,
又∵AB⊥CD,
∴∠AOD=∠BOD=90°,
∴∠2=90°﹣∠EOD=57°,∠BOE=90°+∠EOD=123°.
故答案为:57°,123°.
15.解:与∠1是同位角的是∠4,与∠1是内错角的是∠2,
故答案为:∠4;∠2.
16.解:∵∠1=∠2(已知),
∠1=∠3(对顶角相等),
∴∠2=∠3(等量代换),
∴EC∥DB(同位角相等,两直线平行),
∴∠C=∠ABD
(两直线平行,同位角相等),
又∵∠C=∠D(已知),
∴∠D=∠ABD(等量代换),
∴AC∥DF(内错角相等,两直线平行).
故答案为:对顶角相等;BD;CE;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行.
17.解:∵BD平分∠ABC,
∴∠ABD=∠EBD,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠BDE=∠EBD,
∴BE=DE,
∴△BDE是等腰三角形三角形.
故答案为:等腰.
18.解:如图所示:
①当4条直线经过同一个点时,
有1个交点;
②当3条直线经过同一个点,第4条不经过该点时,
有4个交点;
③当4条直线不经过同一点时,
有6个交点.
综上所述,4条直线相交最多有6个交点.
故答案为:6.
19.解:∵CD⊥AB,
∴线段CD的长度表示点C到AB的距离.
故答案为;CD.
20.解:∵管道拐弯前后的方向保持不变,
∴管道的两个拐角∠α=∠β.
故答案为:内错角相等,两直线平行.
三.解答题(共7小题)
21.解:如图,∠1与∠C是直线DE、BC被直线AC所截形成的同位角,∠2与∠B是直线DE、BC被直线AB所截形成的同位角,∠3与∠C是直线DF、
AC被直线BC所截形成的同位角.
22.解:如图,∵∠1+∠2+∠3=180°,∠1=100°,∠2=30°,
∴∠3=50°,
∴∠6=∠3=50°.
又∵∠FOC=90°,
∴∠3+∠4=90°,
∴∠4=40°.
∵∠FOC+∠5=180°,
∴∠5=90°.
综上所述,∠3,∠4,∠5,∠6的度数分别是:50°、40°、90°、50°.
23.解:∵CD⊥AB于点D,
∴BC>CD;
∵∠BCA=90°,
∴AB>BC;
∴AB>BC>CD.
24.解:AB∥CD的条件为∠7=∠8或∠3=∠4或∠BAD+∠ADC=180°或∠ABC+∠BCD=180°或∠FAB=∠FDC或∠EDC=∠EAB.
25.解:(1)如图,在矩形ABB1A1中,A1B1∥AB,A1A⊥AB;
在矩形A1B1C1D1中,A1D1⊥C1D1;
在矩形ABCD中,AD∥BC.
故答案分别是:∥,⊥,⊥,∥;
(2)根据图示知,直线A1B1与BC不在同一平面内,所以它们虽然没有交点,但是它们也不平行.
故答案是:不是,同一平面.
26.解:能.理由如下:
9条直线,任意两条都不平行,最多交点的个数是==36,
∵36>29,
∴能出现29个交点,
安排如下:先使4条直线相交于一点P,另外5条直线两两相交最多可得=10个交点,
与前四条直线相交最多可得5×4=20个交点,
让其中两个点重合为点O,所以交点减少1个,
交点个数一共有10+20﹣1=29个.
故能做到.
27.证明:过E作EF∥AB
交BC于点F,
∴∠ABE=∠FEB,
∵AB∥CD,
∴EF∥CD,∠ABC+∠BCD=180°,
∴∠DCE=∠FEC,
∵BE⊥CE,
∴∠BEF+∠CEF=∠ABE+∠DCE=90°,
∴∠EBC+∠ECB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠DCE=∠BCE,
∴CE平分∠BCD.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
