2020-2021学年华东师大新版八年级上册数学《第13章 全等三角形》单元测试题(Word版 含解析)
文档属性
| 名称 | 2020-2021学年华东师大新版八年级上册数学《第13章 全等三角形》单元测试题(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 220.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 20:24:02 | ||
图片预览



文档简介
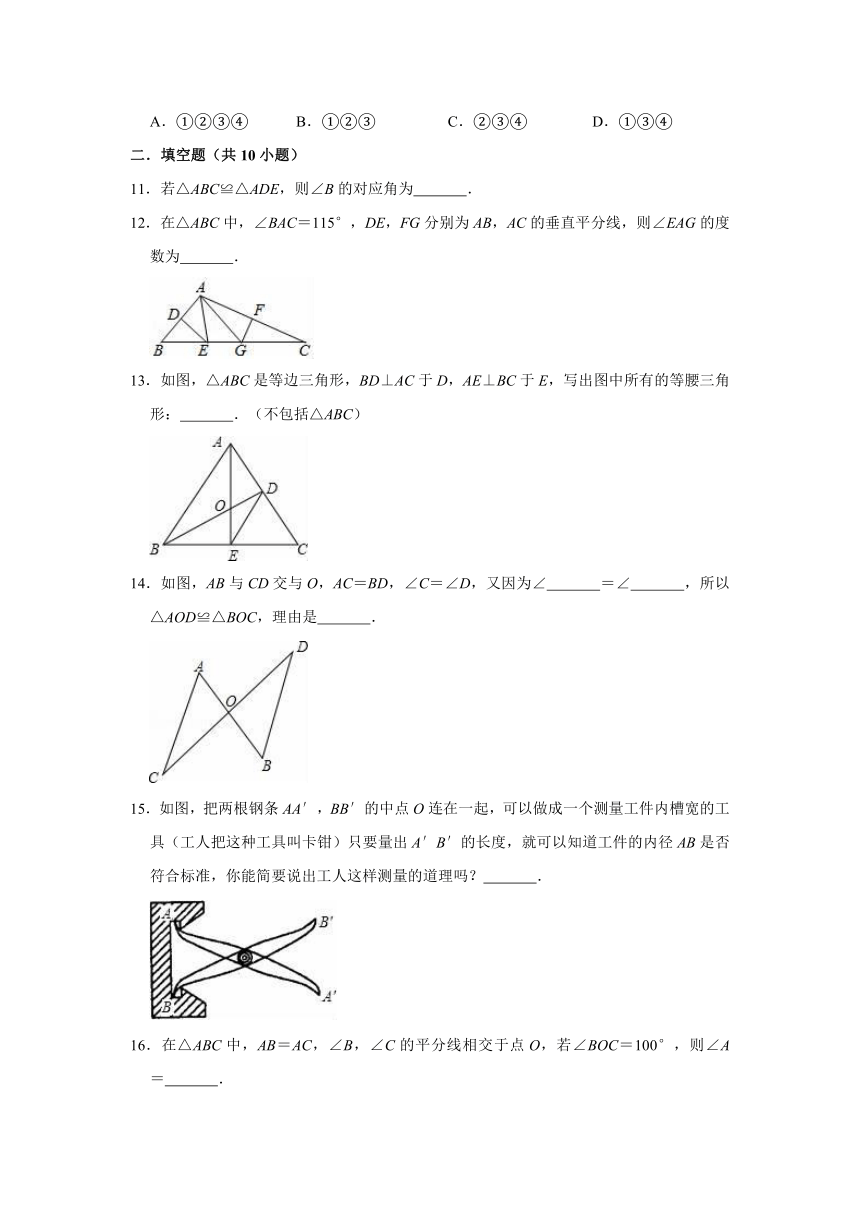
2020-2021学年华东师大新版八年级上册数学《第13章
全等三角形》单元测试题
一.选择题(共10小题)
1.A、B、C、D、E五支球队进行单循环比赛(每两支球队间都要进行一场比赛),当比赛进行到一定阶段时,统计A、B、C、D四个球队已赛过的场数,依次为A队4场,B队3场,C队2场,D队1场,这时,E队已赛过的场数是( )?
A.1
B.2
C.3?
D.4?
2.已知△ABC≌△A′C′B′,∠B与∠C′,∠C与∠B′是对应角,那么下列说法中:①BC=C′B′;②∠C的平分线与∠B的平分线相等;③AC上的高与A′B′边上的高相等;④AB上的中线与A′B′边上的中线相等,其中正确的说法的个数( )
A.1个
B.2个
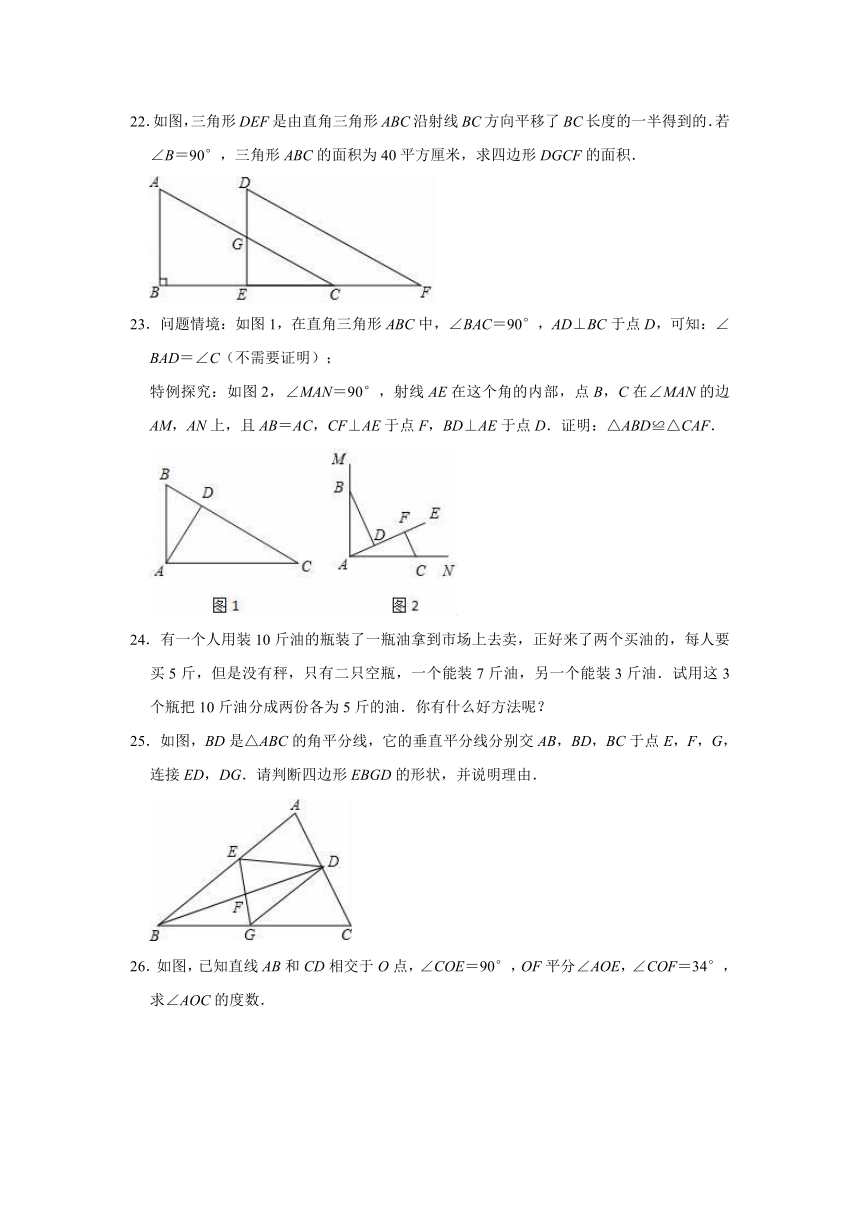
C.3个
D.4个
3.如图,AB=AC,AD=AE,∠BAC=60°,∠C=25°,则∠BMD的度数为( )
A.50°
B.65°
C.70°
D.85°
4.下列条件不能证明两个直角三角形全等的是( )
A.斜边和一直角边对应相等
B.两锐角对应相等
C.两条直角边对应相等
D.斜边和一锐角对应相等
5.举反例说明“一个角的余角大于这个角”是假命题,错误的是( )
A.设这个角是45°
B.设这个角是80°
C.设这个角是30°
D.设这个角是50°
6.如图中,在△ABC中画出AC边上的高正确的是( )
A.
B.
C.
D.
7.如图,在△ABC中,∠C=90°,AB的垂直平分线分别交BC,AB于点D,E,若∠DAB=∠CAD,则∠B=( )
A.45°
B.40°
C.35°
D.30°
8.如图所示,在△ABC中,AB=AC,OA=OB=OC,且∠OBC=2∠OBA,则∠BAC的度数为( )
A.22.5°
B.45°
C.36°
D.25°
9.如图,△AOB≌△COD,A和C,B和D是对应顶点,若BO=8,AO=2,AB=7,则AD的长为( )
A.10
B.8
C.5
D.不能确定
10.如图,在∠BAC的两边上截取AB=AC,AD=AE.连接BD,EC交于点P,则下列结论正确的是( )
①△ABD≌△ACE;②△BEP≌△CDP;③△APB≌△APC;④△APE≌△APD.
A.①②③④
B.①②③
C.②③④
D.①③④
二.填空题(共10小题)
11.若△ABC≌△ADE,则∠B的对应角为
.
12.在△ABC中,∠BAC=115°,DE,FG分别为AB,AC的垂直平分线,则∠EAG的度数为
.
13.如图,△ABC是等边三角形,BD⊥AC于D,AE⊥BC于E,写出图中所有的等腰三角形:
.(不包括△ABC)
14.如图,AB与CD交与O,AC=BD,∠C=∠D,又因为∠
=∠
,所以△AOD≌△BOC,理由是
.
15.如图,把两根钢条AA′,BB′的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳)只要量出A′B′的长度,就可以知道工件的内径AB是否符合标准,你能简要说出工人这样测量的道理吗?
.
16.在△ABC中,AB=AC,∠B,∠C的平分线相交于点O,若∠BOC=100°,则∠A=
.
17.4个人进行游泳比赛,赛前A,B,C,D等4名选手进行预测,A说:“我肯定得第一名”,B说:“我绝对不会得最后一名”,C说:“我不可能得第一名,也不会得最后一名”,D说:“那只有我是最后一名!”,比赛揭晓后,发现他们之中只有一位预测错误,预测错误的人是
.
18.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②BD=DC;③△ABC是等边三角形;④AC=3BF,其中正确的结论有
(写出序号即可).
19.用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是三角形全等,则判定三角形全等的依据是
.
20.如图,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,那么图中的全等三角形有
对.
三.解答题(共7小题)
21.如图,AB=AC,AD=AE,BD=CE.求证:∠BAC=∠DAE.
22.如图,三角形DEF是由直角三角形ABC沿射线BC方向平移了BC长度的一半得到的.若∠B=90°,三角形ABC的面积为40平方厘米,求四边形DGCF的面积.
23.问题情境:如图1,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图2,∠MAN=90°,射线AE在这个角的内部,点B,C在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF.
24.有一个人用装10斤油的瓶装了一瓶油拿到市场上去卖,正好来了两个买油的,每人要买5斤,但是没有秤,只有二只空瓶,一个能装7斤油,另一个能装3斤油.试用这3个瓶把10斤油分成两份各为5斤的油.你有什么好方法呢?
25.如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.请判断四边形EBGD的形状,并说明理由.
26.如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=34°,求∠AOC的度数.
27.如图,在△ABC中,D是BC边上一点,且BA=BD,∠DAC=∠B,∠C=50°.求∠BAC的度数.
参考答案与试题解析
一.选择题(共10小题)
1.解:A、B、C、D、E五支球队进行单循环比赛,已知A队赛过4场,所以A队必须和B、C、D、E这四个球队各赛一场,
已知B队赛过3场,B队已和A队赛过1场,那么B队只能和C、D、E中的两个队比赛,
又知D队只赛过一场(也就是和A队赛过的一场),
所以B队必须和C、E各赛1场,这样满足C队赛过2场,从而推断E队赛过2场.
故选:B.
2.解:∵△ABC≌△A′C′B′
∴BC=C′B′,AC上的高与A′B′边上的高相等.
①、③项正确.
故选:B.
3.证明:∵∠BAC=60°,∠C=25°,
∴∠BDC=25°+60°=85°,
在△AEB和△ADC中,
,
∴△AEB≌△ADC(SAS),
∴∠B=∠C=25°,
∴∠DNB=180°﹣25°﹣85°=70°,
故选:C.
4.A、符合HL,能判定全等;
B、两锐角对应相等不能判定出这两个直角三角形全等;
C、知道两直角边,可以求得第三边,从而利用SSS,能判定全等;
D、知道斜边和一锐角,可以推出另一角的度数,符合AAS,能判定全等.
故选:B.
5.解:设一个角是30°,
那么这个角的余角是:90°﹣30°=60°,
∵30°<60°,
∴“一个角的余角大于这个角”是假命题,
故选:C.
6.解:根据三角形高线的定义,AC边上的高是过点B向AC作垂线垂足为E,
纵观各图形,B、C、D都不符合高线的定义,
A符合高线的定义.
故选:A.
7.解:∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B,
∵∠DAB=∠CAD,
∴∠DAB=∠CAD=∠B,
∵∠C=90°,
∴∠DAB=∠CAD=∠B=30°,
故选:D.
8.解:∵OA=OB=OC,
∴∠OBC=∠OCB,∠OBA=∠OAB,∠OCA=∠OAC,
设∠OBA=x,则∠OBC=2x,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABC+∠ACB+∠BAC=180°,
∴2x+x+2x+x+x+x=180°,
解得x=22.5°,
∴∠BAC=45°,
故选:B.
9.解:∵△AOB≌△COD,A和C,B和D是对应顶点,BO=8,AO=2,AB=7,
∴OD=OB=8,
∴AD=2+8=10,
故选:A.
10.解:在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),故①正确;
∴∠B=∠C,
∵AB=AC,AD=AE,
∴BE=CD,
在△BEP和△CDP中,
,
∴△BEP≌△CDP(AAS),故②正确;
∴BP=CP,
在APB和△APC中,
,
∴APB≌△APC(SSS),故③正确;
∴∠BAP=∠CAP,
∴∠EAP=∠DAP,
在△APE和△APD中,
,
∴△APE≌△APD(SAS),故④正确;
故选:A.
二.填空题(共10小题)
11.解:∵△ABC≌△ADE,
∴∠B的对应角是∠D,
故答案为:∠D.
12.解:∵∠BAC=115°,
∴∠B+∠C=180°﹣115°=65°,
∵DE,FG分别为AB,AC的垂直平分线,
∴EA=EB,GA=GC,
∴∠EAB=∠B,∠GAC=∠C,
∴∠EAB+∠GAC=∠B+∠C=65°,
∴∠EAG=∠BAC﹣(∠EAB+∠GAC)=50°,
故答案为:50°.
13.解:∵△ABC是等边三角形,BD⊥AC于D,AE⊥BC于E
∴∠ABO=∠BAO=30°
∴△ABO是等腰三角形;
∵△ABC的三条角平分线交于一点,这点与三边的距离相等
∴OE=OD
∴△OED是等腰三角形;
∵BD⊥AC,AE⊥BC
∴∠CED=∠CDE
∴△CDE是等腰三角形;
∵∠DEA=∠DAE=30°
∴△ADE是等腰三角形.
根据直角三角形斜边上的中线等于斜边的一半知:ED=BE,
∴△BDE是等腰三角形
故答案为△ABO、△OED、△CDE、△ADE、△BDE.
14.解:AB与CD交与O,AC=BD,∠C=∠D,又因为∠AOC=∠BOD,所以△AOD≌△BOC,理由是AAS,
故答案为:AOC;BOD;AAS
15.解:此工具是根据三角形全等制作而成的.
∵O是AA′,BB′的中点,
∴AO=A′O,BO=B′O,
又∵∠AOB与∠A′OB′是对顶角,
∴∠AOB=∠A′OB′,
在△AOB和△A′OB′中,
∵,
∴△AOB≌△A′OB′(SAS),
∴A′B′=AB,
∴只要量出A′B′的长度,就可以知道工作的内径AB是否符合标准.
16.解:如图,
∵∠BOC=100°,
∴∠OBC+∠OCB=80°,
∵∠ABC与∠ACB的平分线相交于O点,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=160°,
∴∠BAC=20°.
故答案为:20°.
17.解:如果A错,则B为第一,C为第二,D为最后一名,所以A是错的.
如果B错,则B最后,D也错,出现矛盾;
如果C错,则C是第一或最后一名,与A第一、D最后,矛盾;
如果D错,其他都对的话,则没有最后一名;
故答案为:A.
18.解:∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD是△ABC的角平分线,
∴BD=CD,AD⊥BC,故②正确,
无法得出BC=AC,故③错误;
在△CDE和△BDF中,
,
∴△CDE≌△BDF(ASA),
∴DE=DF,CE=BF,故①正确;
∵AE=2BF,
∴AC=3BF,故④正确.
故答案为:①②④.
19.解:由作图可知,OC=OD,O′C=O′D′,CD=C′D′,
∴△DOC≌△D′O′C′(SSS),
∴∠AOB=∠A′O′B′,
故答案为:SSS.
20.解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在△ABD和△ACD中,
∵,
∴△ABD≌△ACD(SAS);
∴∠B=∠C,∠BAD=∠CAD,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠AED=∠AFD=∠CFD=90°,
∴△BDE≌△CDF,△ADE≌△ADF.
全等三角形有3对;
故答案为3.
三.解答题(共7小题)
21.证明:在△ADB和△AEC中,,
∴△ADB≌△AEC(SSS).
∴∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
22.解:由平移的性质可知,三角形DEF的面积=三角形ABC的面积=40平方厘米,GE∥AB,CE=BC,
∴△CGE∽△CAB,
∴=()2=,
∴三角形CGE的面积=10平方厘米,
∴四边形DGCF的面积=40﹣10=30(平方厘米).
23.问题情境:∵∠BAC=90°
∴∠BAD+∠B=90°,
∵AD⊥BC于点D,
∴∠ADB=∠ADC=90°,
∴∠B+∠C=90°,
∴∠BAD=∠C;
特例探究:证明:∵CF⊥AE,BD⊥AE,∠MAN=90°,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°,∠ABD+∠CAF=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
∵,
∴△ABD≌△CAF(AAS).
24.解:先倒满7斤瓶,再分两次从7斤瓶倒满3斤瓶,3斤瓶每次都倒回10斤瓶,
再将7斤瓶中的1斤倒入3斤瓶中,再将7斤瓶倒满,再将7斤瓶中多余的2斤倒入3斤瓶中,
此时7斤瓶中刚好5斤,最后将3斤中的油倒回10斤瓶中就实现了.
25.解:四边形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形.
26.解:∵∠COE=90°,∠COF=34°,
∴∠EOF=90°﹣34°=56°.
∵OF平分∠AOE,
∴∠AOE=∠EOF=56°.
∴∠AOC=∠AOF﹣∠COF=56°﹣34°=22°.
27.解:设∠DAC=x°,则∠B=2x°,∠BDA=∠C+∠DAC=50°+x°.
∵BD=BA,
∴∠BAD=∠BDA=50°+x°,
∵∠B+∠BAD+∠BDA=180°,
即2x+50+x+50+x=180,
解得x=20.
∴∠BAD=∠BDA=50°+20°=70°,
∴∠BAC=∠BAD+∠DAC=70°+20°=90°.
全等三角形》单元测试题
一.选择题(共10小题)
1.A、B、C、D、E五支球队进行单循环比赛(每两支球队间都要进行一场比赛),当比赛进行到一定阶段时,统计A、B、C、D四个球队已赛过的场数,依次为A队4场,B队3场,C队2场,D队1场,这时,E队已赛过的场数是( )?
A.1
B.2
C.3?
D.4?
2.已知△ABC≌△A′C′B′,∠B与∠C′,∠C与∠B′是对应角,那么下列说法中:①BC=C′B′;②∠C的平分线与∠B的平分线相等;③AC上的高与A′B′边上的高相等;④AB上的中线与A′B′边上的中线相等,其中正确的说法的个数( )
A.1个
B.2个
C.3个
D.4个
3.如图,AB=AC,AD=AE,∠BAC=60°,∠C=25°,则∠BMD的度数为( )
A.50°
B.65°
C.70°
D.85°
4.下列条件不能证明两个直角三角形全等的是( )
A.斜边和一直角边对应相等
B.两锐角对应相等
C.两条直角边对应相等
D.斜边和一锐角对应相等
5.举反例说明“一个角的余角大于这个角”是假命题,错误的是( )
A.设这个角是45°
B.设这个角是80°
C.设这个角是30°
D.设这个角是50°
6.如图中,在△ABC中画出AC边上的高正确的是( )
A.
B.
C.
D.
7.如图,在△ABC中,∠C=90°,AB的垂直平分线分别交BC,AB于点D,E,若∠DAB=∠CAD,则∠B=( )
A.45°
B.40°
C.35°
D.30°
8.如图所示,在△ABC中,AB=AC,OA=OB=OC,且∠OBC=2∠OBA,则∠BAC的度数为( )
A.22.5°
B.45°
C.36°
D.25°
9.如图,△AOB≌△COD,A和C,B和D是对应顶点,若BO=8,AO=2,AB=7,则AD的长为( )
A.10
B.8
C.5
D.不能确定
10.如图,在∠BAC的两边上截取AB=AC,AD=AE.连接BD,EC交于点P,则下列结论正确的是( )
①△ABD≌△ACE;②△BEP≌△CDP;③△APB≌△APC;④△APE≌△APD.
A.①②③④
B.①②③
C.②③④
D.①③④
二.填空题(共10小题)
11.若△ABC≌△ADE,则∠B的对应角为
.
12.在△ABC中,∠BAC=115°,DE,FG分别为AB,AC的垂直平分线,则∠EAG的度数为
.
13.如图,△ABC是等边三角形,BD⊥AC于D,AE⊥BC于E,写出图中所有的等腰三角形:
.(不包括△ABC)
14.如图,AB与CD交与O,AC=BD,∠C=∠D,又因为∠
=∠
,所以△AOD≌△BOC,理由是
.
15.如图,把两根钢条AA′,BB′的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳)只要量出A′B′的长度,就可以知道工件的内径AB是否符合标准,你能简要说出工人这样测量的道理吗?
.
16.在△ABC中,AB=AC,∠B,∠C的平分线相交于点O,若∠BOC=100°,则∠A=
.
17.4个人进行游泳比赛,赛前A,B,C,D等4名选手进行预测,A说:“我肯定得第一名”,B说:“我绝对不会得最后一名”,C说:“我不可能得第一名,也不会得最后一名”,D说:“那只有我是最后一名!”,比赛揭晓后,发现他们之中只有一位预测错误,预测错误的人是
.
18.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②BD=DC;③△ABC是等边三角形;④AC=3BF,其中正确的结论有
(写出序号即可).
19.用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是三角形全等,则判定三角形全等的依据是
.
20.如图,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,那么图中的全等三角形有
对.
三.解答题(共7小题)
21.如图,AB=AC,AD=AE,BD=CE.求证:∠BAC=∠DAE.
22.如图,三角形DEF是由直角三角形ABC沿射线BC方向平移了BC长度的一半得到的.若∠B=90°,三角形ABC的面积为40平方厘米,求四边形DGCF的面积.
23.问题情境:如图1,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图2,∠MAN=90°,射线AE在这个角的内部,点B,C在∠MAN的边AM,AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF.
24.有一个人用装10斤油的瓶装了一瓶油拿到市场上去卖,正好来了两个买油的,每人要买5斤,但是没有秤,只有二只空瓶,一个能装7斤油,另一个能装3斤油.试用这3个瓶把10斤油分成两份各为5斤的油.你有什么好方法呢?
25.如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.请判断四边形EBGD的形状,并说明理由.
26.如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=34°,求∠AOC的度数.
27.如图,在△ABC中,D是BC边上一点,且BA=BD,∠DAC=∠B,∠C=50°.求∠BAC的度数.
参考答案与试题解析
一.选择题(共10小题)
1.解:A、B、C、D、E五支球队进行单循环比赛,已知A队赛过4场,所以A队必须和B、C、D、E这四个球队各赛一场,
已知B队赛过3场,B队已和A队赛过1场,那么B队只能和C、D、E中的两个队比赛,
又知D队只赛过一场(也就是和A队赛过的一场),
所以B队必须和C、E各赛1场,这样满足C队赛过2场,从而推断E队赛过2场.
故选:B.
2.解:∵△ABC≌△A′C′B′
∴BC=C′B′,AC上的高与A′B′边上的高相等.
①、③项正确.
故选:B.
3.证明:∵∠BAC=60°,∠C=25°,
∴∠BDC=25°+60°=85°,
在△AEB和△ADC中,
,
∴△AEB≌△ADC(SAS),
∴∠B=∠C=25°,
∴∠DNB=180°﹣25°﹣85°=70°,
故选:C.
4.A、符合HL,能判定全等;
B、两锐角对应相等不能判定出这两个直角三角形全等;
C、知道两直角边,可以求得第三边,从而利用SSS,能判定全等;
D、知道斜边和一锐角,可以推出另一角的度数,符合AAS,能判定全等.
故选:B.
5.解:设一个角是30°,
那么这个角的余角是:90°﹣30°=60°,
∵30°<60°,
∴“一个角的余角大于这个角”是假命题,
故选:C.
6.解:根据三角形高线的定义,AC边上的高是过点B向AC作垂线垂足为E,
纵观各图形,B、C、D都不符合高线的定义,
A符合高线的定义.
故选:A.
7.解:∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B,
∵∠DAB=∠CAD,
∴∠DAB=∠CAD=∠B,
∵∠C=90°,
∴∠DAB=∠CAD=∠B=30°,
故选:D.
8.解:∵OA=OB=OC,
∴∠OBC=∠OCB,∠OBA=∠OAB,∠OCA=∠OAC,
设∠OBA=x,则∠OBC=2x,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABC+∠ACB+∠BAC=180°,
∴2x+x+2x+x+x+x=180°,
解得x=22.5°,
∴∠BAC=45°,
故选:B.
9.解:∵△AOB≌△COD,A和C,B和D是对应顶点,BO=8,AO=2,AB=7,
∴OD=OB=8,
∴AD=2+8=10,
故选:A.
10.解:在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),故①正确;
∴∠B=∠C,
∵AB=AC,AD=AE,
∴BE=CD,
在△BEP和△CDP中,
,
∴△BEP≌△CDP(AAS),故②正确;
∴BP=CP,
在APB和△APC中,
,
∴APB≌△APC(SSS),故③正确;
∴∠BAP=∠CAP,
∴∠EAP=∠DAP,
在△APE和△APD中,
,
∴△APE≌△APD(SAS),故④正确;
故选:A.
二.填空题(共10小题)
11.解:∵△ABC≌△ADE,
∴∠B的对应角是∠D,
故答案为:∠D.
12.解:∵∠BAC=115°,
∴∠B+∠C=180°﹣115°=65°,
∵DE,FG分别为AB,AC的垂直平分线,
∴EA=EB,GA=GC,
∴∠EAB=∠B,∠GAC=∠C,
∴∠EAB+∠GAC=∠B+∠C=65°,
∴∠EAG=∠BAC﹣(∠EAB+∠GAC)=50°,
故答案为:50°.
13.解:∵△ABC是等边三角形,BD⊥AC于D,AE⊥BC于E
∴∠ABO=∠BAO=30°
∴△ABO是等腰三角形;
∵△ABC的三条角平分线交于一点,这点与三边的距离相等
∴OE=OD
∴△OED是等腰三角形;
∵BD⊥AC,AE⊥BC
∴∠CED=∠CDE
∴△CDE是等腰三角形;
∵∠DEA=∠DAE=30°
∴△ADE是等腰三角形.
根据直角三角形斜边上的中线等于斜边的一半知:ED=BE,
∴△BDE是等腰三角形
故答案为△ABO、△OED、△CDE、△ADE、△BDE.
14.解:AB与CD交与O,AC=BD,∠C=∠D,又因为∠AOC=∠BOD,所以△AOD≌△BOC,理由是AAS,
故答案为:AOC;BOD;AAS
15.解:此工具是根据三角形全等制作而成的.
∵O是AA′,BB′的中点,
∴AO=A′O,BO=B′O,
又∵∠AOB与∠A′OB′是对顶角,
∴∠AOB=∠A′OB′,
在△AOB和△A′OB′中,
∵,
∴△AOB≌△A′OB′(SAS),
∴A′B′=AB,
∴只要量出A′B′的长度,就可以知道工作的内径AB是否符合标准.
16.解:如图,
∵∠BOC=100°,
∴∠OBC+∠OCB=80°,
∵∠ABC与∠ACB的平分线相交于O点,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=160°,
∴∠BAC=20°.
故答案为:20°.
17.解:如果A错,则B为第一,C为第二,D为最后一名,所以A是错的.
如果B错,则B最后,D也错,出现矛盾;
如果C错,则C是第一或最后一名,与A第一、D最后,矛盾;
如果D错,其他都对的话,则没有最后一名;
故答案为:A.
18.解:∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD是△ABC的角平分线,
∴BD=CD,AD⊥BC,故②正确,
无法得出BC=AC,故③错误;
在△CDE和△BDF中,
,
∴△CDE≌△BDF(ASA),
∴DE=DF,CE=BF,故①正确;
∵AE=2BF,
∴AC=3BF,故④正确.
故答案为:①②④.
19.解:由作图可知,OC=OD,O′C=O′D′,CD=C′D′,
∴△DOC≌△D′O′C′(SSS),
∴∠AOB=∠A′O′B′,
故答案为:SSS.
20.解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在△ABD和△ACD中,
∵,
∴△ABD≌△ACD(SAS);
∴∠B=∠C,∠BAD=∠CAD,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠AED=∠AFD=∠CFD=90°,
∴△BDE≌△CDF,△ADE≌△ADF.
全等三角形有3对;
故答案为3.
三.解答题(共7小题)
21.证明:在△ADB和△AEC中,,
∴△ADB≌△AEC(SSS).
∴∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
22.解:由平移的性质可知,三角形DEF的面积=三角形ABC的面积=40平方厘米,GE∥AB,CE=BC,
∴△CGE∽△CAB,
∴=()2=,
∴三角形CGE的面积=10平方厘米,
∴四边形DGCF的面积=40﹣10=30(平方厘米).
23.问题情境:∵∠BAC=90°
∴∠BAD+∠B=90°,
∵AD⊥BC于点D,
∴∠ADB=∠ADC=90°,
∴∠B+∠C=90°,
∴∠BAD=∠C;
特例探究:证明:∵CF⊥AE,BD⊥AE,∠MAN=90°,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°,∠ABD+∠CAF=90°,
∴∠ABD=∠CAF,
在△ABD和△CAF中,
∵,
∴△ABD≌△CAF(AAS).
24.解:先倒满7斤瓶,再分两次从7斤瓶倒满3斤瓶,3斤瓶每次都倒回10斤瓶,
再将7斤瓶中的1斤倒入3斤瓶中,再将7斤瓶倒满,再将7斤瓶中多余的2斤倒入3斤瓶中,
此时7斤瓶中刚好5斤,最后将3斤中的油倒回10斤瓶中就实现了.
25.解:四边形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形.
26.解:∵∠COE=90°,∠COF=34°,
∴∠EOF=90°﹣34°=56°.
∵OF平分∠AOE,
∴∠AOE=∠EOF=56°.
∴∠AOC=∠AOF﹣∠COF=56°﹣34°=22°.
27.解:设∠DAC=x°,则∠B=2x°,∠BDA=∠C+∠DAC=50°+x°.
∵BD=BA,
∴∠BAD=∠BDA=50°+x°,
∵∠B+∠BAD+∠BDA=180°,
即2x+50+x+50+x=180,
解得x=20.
∴∠BAD=∠BDA=50°+20°=70°,
∴∠BAC=∠BAD+∠DAC=70°+20°=90°.
