人教版数学九年级上册:24.1.4圆周角-课件(34张)
文档属性
| 名称 | 人教版数学九年级上册:24.1.4圆周角-课件(34张) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 21:46:45 | ||
图片预览




文档简介
复习备用
弧、弦、圆心角
1、圆是中心对称图形,对称中心是: .
2、圆心角: .
3、在同圆或等圆中
圆心角相等
两条弧相等
两条弦相等
知一推二
弦心距相等,两条弦也相等
情景引入
哪一点射门最佳?
人教版九年级数学上册
第二十四章 圆
24.1 圆的有关性质
1.4 圆周角(1)圆周角定理
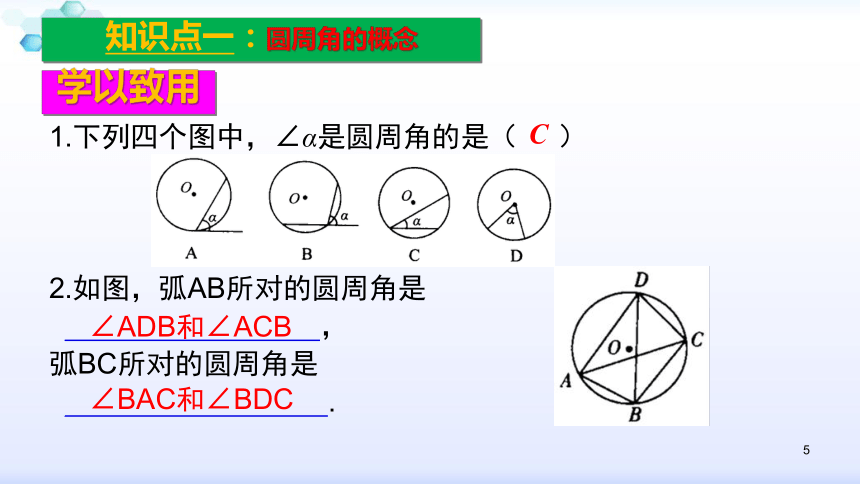
知识点一:圆周角的概念
如图:在圆中,除圆心角外,还有一类角(如图中的∠ACB),它的顶点在圆上①,并且两边都与圆相交②,
新知探究
C
A
O
B
我们把这样的角叫做圆周角.
学以致用
1.下列四个图中,∠α是圆周角的是( )
2.如图,弧AB所对的圆周角是
,
弧BC所对的圆周角是
.
C
∠ADB和∠ACB
知识点一:圆周角的概念
∠BAC和∠BDC
归纳总结
圆周角必须具备两个条件:
①顶点在圆上,
②两边都与圆相交.
知识点一:圆周角的概念
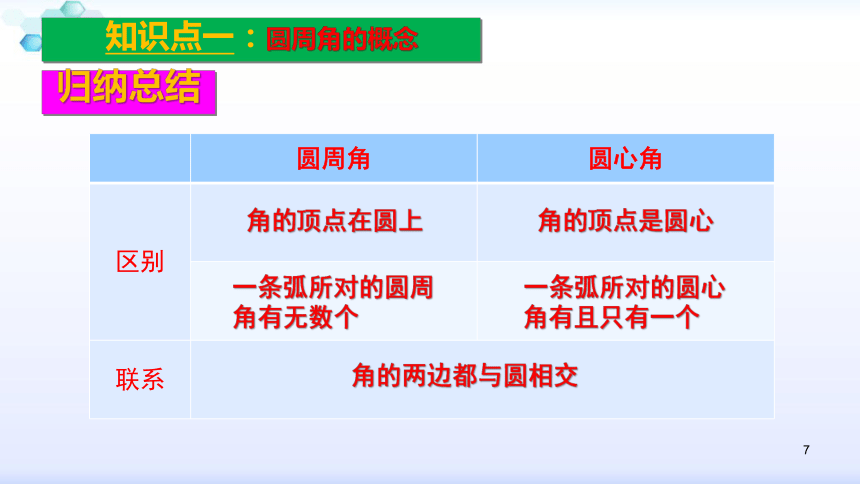
归纳总结
知识点一:圆周角的概念
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
圆周角
圆心角
区别
联系
角的顶点在圆上
角的顶点是圆心
一条弧所对的圆周角有无数个
一条弧所对的圆心角有且只有一个
角的两边都与圆相交
新知探究
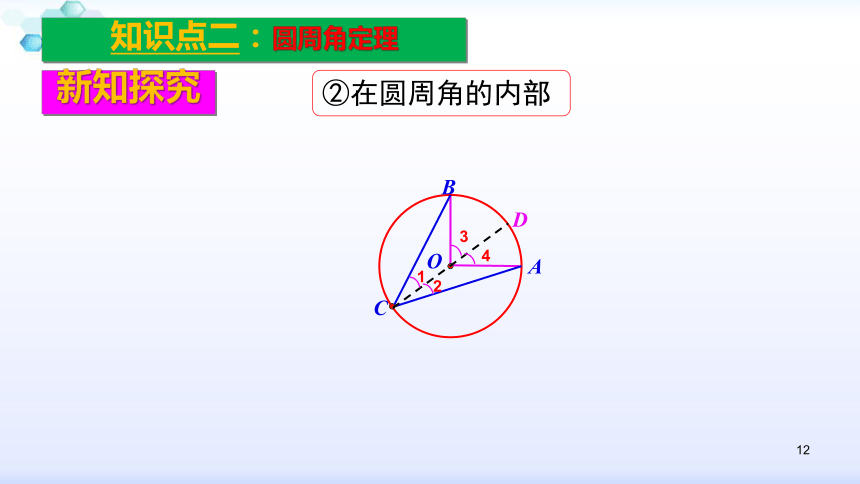
知识点二:圆周角定理
问题:如图,连接AO,BO,得到
圆心角∠AOB.
可以发现,∠ACB与∠AOB对着同
一条弧AB,它们之间存在什么关系
呢?
C
A
O
B
新知探究
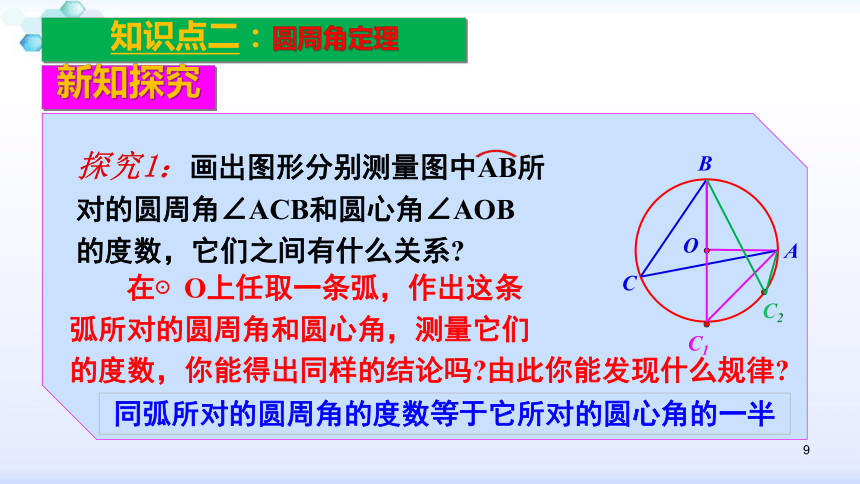
探究1:画出图形分别测量图中AB所
对的圆周角∠ACB和圆心角∠AOB
的度数,它们之间有什么关系?
知识点二:圆周角定理
C
A
O
B
在⊙O上任取一条弧,作出这条
弧所对的圆周角和圆心角,测量它们
的度数,你能得出同样的结论吗?由此你能发现什么规律?
同弧所对的圆周角的度数等于它所对的圆心角的一半
C1
C2
新知探究
知识点二:圆周角定理
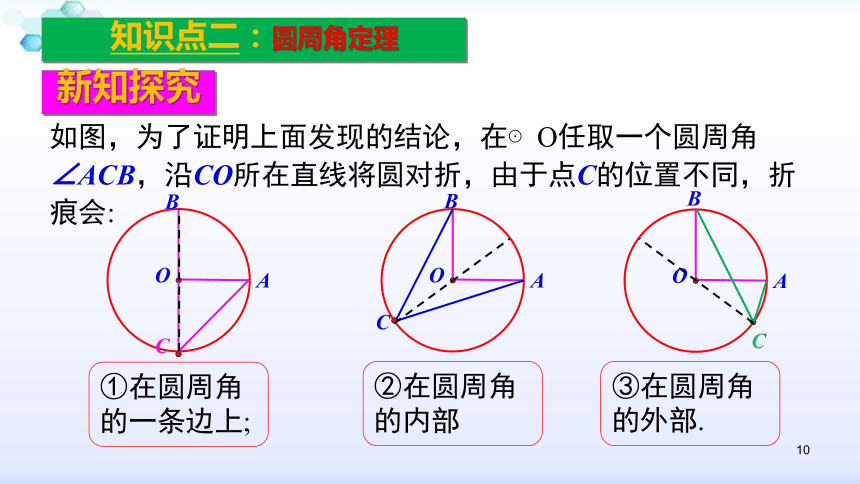
如图,为了证明上面发现的结论,在⊙O任取一个圆周角∠ACB,沿CO所在直线将圆对折,由于点C的位置不同,折痕会:
①在圆周角的一条边上;
②在圆周角的内部
③在圆周角的外部.
A
O
B
C
A
O
B
C
C
A
O
B
新知探究
知识点二:圆周角定理
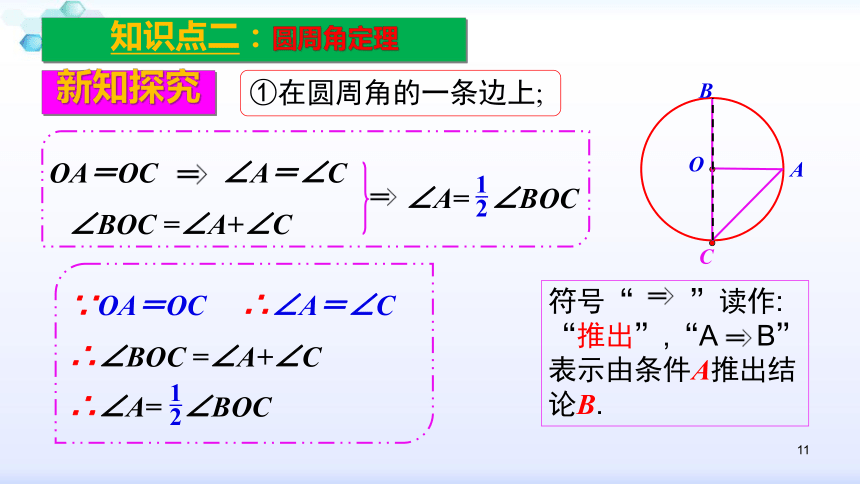
①在圆周角的一条边上;
A
O
B
C
∠A= ∠BOC
1
2
∠BOC =∠A+∠C
OA=OC ∠A=∠C
符号“ ”读作:
“推出”,“A B”表示由条件A推出结论B.
∵OA=OC ∴∠A=∠C
∴∠BOC =∠A+∠C
∴∠A= ∠BOC
1
2
新知探究
知识点二:圆周角定理
②在圆周角的内部
C
A
O
B
1
2
3
4
D
新知探究
知识点二:圆周角定理
③在圆周角的外部.
A
O
B
C
D
1
2
归纳总结
知识点二:圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半
圆周角定理
C
A
O
B
几何语言
∵ ∠C是AB所对的一个圆周角
∠AOB是AB所对的一个圆心角
∴∠C= ∠AOB
1
2
归纳总结
知识点二:圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半
化归
圆周角定理
分类讨论
完全归纳法
圆周角定理
化归
学以致用
1.如图,⊙O是△ABC的外接圆,已知∠ABO=30°,则∠ACB的度数为( )
A.40° B.30° C.50° D.60°
2.如图,点A,B,C在⊙O上,点D在⊙O外,下列结论正确的是( )
A.∠C>∠D B.∠C<∠D
C.∠C=∠D D.∠C=2∠D
D
知识点二:圆周角定理
A
A
O
B
C
A
O
B
C
D
学以致用
40°
知识点二:圆周角定理
A
O
B
C
3.如图,⊙O是△ABC的外接圆,∠AOB=80°,AB=AC,则∠ABC= .
4.如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若AB的度数是120°,则∠ACB= .
A
O
B
C
60°
先独立完成导学案互动探究2,再同桌相互交
流,最后小组交流;
合作探究
知识点二:圆周角定理
①弦AB所对的弧有哪几条?
②一条弦所对的圆周角分几类?自己画一画.
A
O
B
归纳总结
定理:一条弧所对的圆周角等于它所对的圆心角的一半.
也可以理解为:①一条弧所对的圆心角是它所对的圆周角的二倍;②圆周角的度数等于它所对的弧的度数的一半.
知识点二:圆周角定理
新知探究
知识点三:圆周角定理的推论
探究2:⑴如图①,比较∠ACB、∠ADB、
∠AEB的大小.
⑵如图②,如果AB=CD,那么∠E
和∠F是什么关系?反过来呢?
O
B
A
D
E
C
①
D
C
E
B
F
A
O
②
你能用一句话概括得到结论吗?
典例讲评
知识点三:圆周角定理的推论
探究2:⑶ 如图③,⊙O1和⊙O2是等圆,
如果AB=CD,那么∠E和∠F是什么关系?
反过来呢?
D
C
E
O1
B
F
A
O2
结合⑴、⑵你能得到什么结论?
归纳总结
同弧或等弧所对的圆周角相等;
在同圆或等圆中,相等的圆周角所对的弧相等.
知识点三:圆周角定理的推论
圆周角定理推理1
几何语言
D
C
E
B
F
A
O
∵ AB=CD
∴∠E=∠F
在⊙O中∵∠E=∠F
∴AB=CD
学以致用
1、如图,在⊙O中,弦AB,CD相交于点P,∠A=40,∠APD=75°,则∠B=( )
A.15°B.40°C.75°D.35°
2.如图,CD⊥AB于点E,若∠B=60°,则∠A= .
知识点三:圆周角定理的推论
D
30°
学以致用
知识点三:圆周角定理的推论
3、下列结论:在同圆或等圆中,①圆心角相等,圆心角所对的弧也相等;②两条弦相等,弦所对的弧也相等;③弦心距弦心距所对的弦相等;④两个圆周角相等,圆周角所对的弧相等;⑤弧相等弧所对的弦相等;
⑥弧相等弧所对的圆周角也相等。
其中正确的有 (填序号).
典例讲评
知识点三:圆周角定理的推论
探究3: 如图,AB是⊙O直径,
你知道∠C、∠D、∠E是什么关系吗?
你能求出它们的度数吗?
如果∠D=90°,AB是直径吗?
O
B
A
D
E
C
你能得到什么结论?
归纳总结
①半圆(或直径)所对的圆周角是90°;
②90°的圆周角所对的弦是直径.
知识点三:圆周角定理的推论
圆周角定理推理2
O
B
A
D
E
C
几何语言
∵ AB是半圆(AB是直径)
∴∠E=90°
∵∠E=90°
∴AB是⊙O的直径
典例讲评
例1:如图,点D是等腰三角形ABC底边
的中点,过点A,B,D作⊙O .
(1)求证:AB是⊙O的直径
(2)延长CB交⊙O于点E,连接DE,求证:DC=DE
证明:(1)连接BD
知识点三:圆周角定理的推论
A
B
C
O
·
D
E
∵BA=BC,AD=DC,∴BD⊥AC,∴∠ADB=90°,∴AB是⊙0的直径
(2)∵BA=BC,∴∠A=∠C.
由圆周角定理得∠A=∠E,
∴∠C=∠E,∴DC=DE.
先独立完成导学案互动探究1、3,
再同桌相互交流,最后小组交流;
合作探究
知识点三:圆周角定理的推论
1.如图,在⊙O中,弦AB=3cm,点C在⊙O上,∠ACB=30°.求⊙O直径.
2.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AC=AB,BD与CD的大小有什么关系?为什么?
A
O
B
C
A
O
B
C
D
学以致用
1、如图,AB是半圆的直径,点D是AC的中点,∠ABC=50°,则∠DAB等于( )
A.55°B.60°C.65°D.70°
2.如图,⊙O的半径为1,AB是⊙O的一条
弦,且AB= ,则弦AB所对的圆周角的度数为( )
A.30? B.60? C.30?或150 ? D.60?或120?
知识点三:圆周角定理的推论
A
O
B
C
D
A
O
B
C
D
学以致用
3、如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,
求BC、AD、BD的长(课本例4)。
知识点三:圆周角定理的推论
C
D
A
O
B
归纳总结
知识点三:圆周角定理的推论
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
文字语言
几何语言
图示
定理
推理
一条弧所对的圆周角等于它所对的圆心角的一半
同弧或等弧所对的圆周角相等;
∵∠C、∠D都是AB所对圆周角
∴∠C=∠D
半圆(或直径)所对的圆周角是90°;
90°的圆周角所对的弦是直径.
∵ AB是半圆(AB是直径)
∴∠C=∠D=90°
∵∠C=90°或∠D=90°
∴AB是⊙O的直径
思维导图
圆周角
1、概念:
2、定理:
3、推理:
同弧或等弧所对的圆周角相等
半圆(或直径)所对的圆周角是90°
90°的圆周角所对的弦是直径
一条弧所对的圆周角等于它所对的圆心角的一半
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
1.课本第88页练习1、3以及习题24.1第5、6、13题
作业布置
弧、弦、圆心角
1、圆是中心对称图形,对称中心是: .
2、圆心角: .
3、在同圆或等圆中
圆心角相等
两条弧相等
两条弦相等
知一推二
弦心距相等,两条弦也相等
情景引入
哪一点射门最佳?
人教版九年级数学上册
第二十四章 圆
24.1 圆的有关性质
1.4 圆周角(1)圆周角定理
知识点一:圆周角的概念
如图:在圆中,除圆心角外,还有一类角(如图中的∠ACB),它的顶点在圆上①,并且两边都与圆相交②,
新知探究
C
A
O
B
我们把这样的角叫做圆周角.
学以致用
1.下列四个图中,∠α是圆周角的是( )
2.如图,弧AB所对的圆周角是
,
弧BC所对的圆周角是
.
C
∠ADB和∠ACB
知识点一:圆周角的概念
∠BAC和∠BDC
归纳总结
圆周角必须具备两个条件:
①顶点在圆上,
②两边都与圆相交.
知识点一:圆周角的概念
归纳总结
知识点一:圆周角的概念
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
圆周角
圆心角
区别
联系
角的顶点在圆上
角的顶点是圆心
一条弧所对的圆周角有无数个
一条弧所对的圆心角有且只有一个
角的两边都与圆相交
新知探究
知识点二:圆周角定理
问题:如图,连接AO,BO,得到
圆心角∠AOB.
可以发现,∠ACB与∠AOB对着同
一条弧AB,它们之间存在什么关系
呢?
C
A
O
B
新知探究
探究1:画出图形分别测量图中AB所
对的圆周角∠ACB和圆心角∠AOB
的度数,它们之间有什么关系?
知识点二:圆周角定理
C
A
O
B
在⊙O上任取一条弧,作出这条
弧所对的圆周角和圆心角,测量它们
的度数,你能得出同样的结论吗?由此你能发现什么规律?
同弧所对的圆周角的度数等于它所对的圆心角的一半
C1
C2
新知探究
知识点二:圆周角定理
如图,为了证明上面发现的结论,在⊙O任取一个圆周角∠ACB,沿CO所在直线将圆对折,由于点C的位置不同,折痕会:
①在圆周角的一条边上;
②在圆周角的内部
③在圆周角的外部.
A
O
B
C
A
O
B
C
C
A
O
B
新知探究
知识点二:圆周角定理
①在圆周角的一条边上;
A
O
B
C
∠A= ∠BOC
1
2
∠BOC =∠A+∠C
OA=OC ∠A=∠C
符号“ ”读作:
“推出”,“A B”表示由条件A推出结论B.
∵OA=OC ∴∠A=∠C
∴∠BOC =∠A+∠C
∴∠A= ∠BOC
1
2
新知探究
知识点二:圆周角定理
②在圆周角的内部
C
A
O
B
1
2
3
4
D
新知探究
知识点二:圆周角定理
③在圆周角的外部.
A
O
B
C
D
1
2
归纳总结
知识点二:圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半
圆周角定理
C
A
O
B
几何语言
∵ ∠C是AB所对的一个圆周角
∠AOB是AB所对的一个圆心角
∴∠C= ∠AOB
1
2
归纳总结
知识点二:圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半
化归
圆周角定理
分类讨论
完全归纳法
圆周角定理
化归
学以致用
1.如图,⊙O是△ABC的外接圆,已知∠ABO=30°,则∠ACB的度数为( )
A.40° B.30° C.50° D.60°
2.如图,点A,B,C在⊙O上,点D在⊙O外,下列结论正确的是( )
A.∠C>∠D B.∠C<∠D
C.∠C=∠D D.∠C=2∠D
D
知识点二:圆周角定理
A
A
O
B
C
A
O
B
C
D
学以致用
40°
知识点二:圆周角定理
A
O
B
C
3.如图,⊙O是△ABC的外接圆,∠AOB=80°,AB=AC,则∠ABC= .
4.如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若AB的度数是120°,则∠ACB= .
A
O
B
C
60°
先独立完成导学案互动探究2,再同桌相互交
流,最后小组交流;
合作探究
知识点二:圆周角定理
①弦AB所对的弧有哪几条?
②一条弦所对的圆周角分几类?自己画一画.
A
O
B
归纳总结
定理:一条弧所对的圆周角等于它所对的圆心角的一半.
也可以理解为:①一条弧所对的圆心角是它所对的圆周角的二倍;②圆周角的度数等于它所对的弧的度数的一半.
知识点二:圆周角定理
新知探究
知识点三:圆周角定理的推论
探究2:⑴如图①,比较∠ACB、∠ADB、
∠AEB的大小.
⑵如图②,如果AB=CD,那么∠E
和∠F是什么关系?反过来呢?
O
B
A
D
E
C
①
D
C
E
B
F
A
O
②
你能用一句话概括得到结论吗?
典例讲评
知识点三:圆周角定理的推论
探究2:⑶ 如图③,⊙O1和⊙O2是等圆,
如果AB=CD,那么∠E和∠F是什么关系?
反过来呢?
D
C
E
O1
B
F
A
O2
结合⑴、⑵你能得到什么结论?
归纳总结
同弧或等弧所对的圆周角相等;
在同圆或等圆中,相等的圆周角所对的弧相等.
知识点三:圆周角定理的推论
圆周角定理推理1
几何语言
D
C
E
B
F
A
O
∵ AB=CD
∴∠E=∠F
在⊙O中∵∠E=∠F
∴AB=CD
学以致用
1、如图,在⊙O中,弦AB,CD相交于点P,∠A=40,∠APD=75°,则∠B=( )
A.15°B.40°C.75°D.35°
2.如图,CD⊥AB于点E,若∠B=60°,则∠A= .
知识点三:圆周角定理的推论
D
30°
学以致用
知识点三:圆周角定理的推论
3、下列结论:在同圆或等圆中,①圆心角相等,圆心角所对的弧也相等;②两条弦相等,弦所对的弧也相等;③弦心距弦心距所对的弦相等;④两个圆周角相等,圆周角所对的弧相等;⑤弧相等弧所对的弦相等;
⑥弧相等弧所对的圆周角也相等。
其中正确的有 (填序号).
典例讲评
知识点三:圆周角定理的推论
探究3: 如图,AB是⊙O直径,
你知道∠C、∠D、∠E是什么关系吗?
你能求出它们的度数吗?
如果∠D=90°,AB是直径吗?
O
B
A
D
E
C
你能得到什么结论?
归纳总结
①半圆(或直径)所对的圆周角是90°;
②90°的圆周角所对的弦是直径.
知识点三:圆周角定理的推论
圆周角定理推理2
O
B
A
D
E
C
几何语言
∵ AB是半圆(AB是直径)
∴∠E=90°
∵∠E=90°
∴AB是⊙O的直径
典例讲评
例1:如图,点D是等腰三角形ABC底边
的中点,过点A,B,D作⊙O .
(1)求证:AB是⊙O的直径
(2)延长CB交⊙O于点E,连接DE,求证:DC=DE
证明:(1)连接BD
知识点三:圆周角定理的推论
A
B
C
O
·
D
E
∵BA=BC,AD=DC,∴BD⊥AC,∴∠ADB=90°,∴AB是⊙0的直径
(2)∵BA=BC,∴∠A=∠C.
由圆周角定理得∠A=∠E,
∴∠C=∠E,∴DC=DE.
先独立完成导学案互动探究1、3,
再同桌相互交流,最后小组交流;
合作探究
知识点三:圆周角定理的推论
1.如图,在⊙O中,弦AB=3cm,点C在⊙O上,∠ACB=30°.求⊙O直径.
2.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AC=AB,BD与CD的大小有什么关系?为什么?
A
O
B
C
A
O
B
C
D
学以致用
1、如图,AB是半圆的直径,点D是AC的中点,∠ABC=50°,则∠DAB等于( )
A.55°B.60°C.65°D.70°
2.如图,⊙O的半径为1,AB是⊙O的一条
弦,且AB= ,则弦AB所对的圆周角的度数为( )
A.30? B.60? C.30?或150 ? D.60?或120?
知识点三:圆周角定理的推论
A
O
B
C
D
A
O
B
C
D
学以致用
3、如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,
求BC、AD、BD的长(课本例4)。
知识点三:圆周角定理的推论
C
D
A
O
B
归纳总结
知识点三:圆周角定理的推论
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
文字语言
几何语言
图示
定理
推理
一条弧所对的圆周角等于它所对的圆心角的一半
同弧或等弧所对的圆周角相等;
∵∠C、∠D都是AB所对圆周角
∴∠C=∠D
半圆(或直径)所对的圆周角是90°;
90°的圆周角所对的弦是直径.
∵ AB是半圆(AB是直径)
∴∠C=∠D=90°
∵∠C=90°或∠D=90°
∴AB是⊙O的直径
思维导图
圆周角
1、概念:
2、定理:
3、推理:
同弧或等弧所对的圆周角相等
半圆(或直径)所对的圆周角是90°
90°的圆周角所对的弦是直径
一条弧所对的圆周角等于它所对的圆心角的一半
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
1.课本第88页练习1、3以及习题24.1第5、6、13题
作业布置
同课章节目录
