2020年秋四川省绵阳市人教版初中数学九年级上册24.1.2 垂直于弦的直径 课后提升训练试卷(word解析版)
文档属性
| 名称 | 2020年秋四川省绵阳市人教版初中数学九年级上册24.1.2 垂直于弦的直径 课后提升训练试卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 446.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 00:00:00 | ||
图片预览


文档简介
2020年秋绵阳南山双语学校
初中数学(人教版)九年级
上册
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
1.下列说法中,不正确的是?( )
A.圆既是轴对称图形,又是中心对称图形
B.圆绕着它的圆心旋转任意角度,都能与自身重合
C.圆的对称轴有无数条,对称中心只有一个
D.圆的每一条直径都是它的对称轴
2.
(2020江苏南通如皋中学期中)如图,在☉O中,AB为弦,OC⊥AB,垂足为点C,若OA=5,OC=3,则弦AB长为?( )
A.4 ????B.6 ????
C.8 ????D.10
3.
(2020福建福州福清期中)如图,☉O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),则OP的最小值是?( )
A.2.5 ????B.3 ????
C.3.5 ????D.4
4.
(2019山东滨州滨城模拟)如图,某下水道的横截面是圆形的,水面CD的宽度为2
m,F是线段CD的中点,EF经过圆心O交☉O于点E,EF=3
m,则☉O的直径是( )
A.?
m ????B.?
m ????
C.?
m ????D.?
m
5.
(2019湖北武汉硚口期中)如图,AB、AC、BC都是☉O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=1,则BC的值为?( )
A.1 ????B.2 ????
C.3 ????D.4
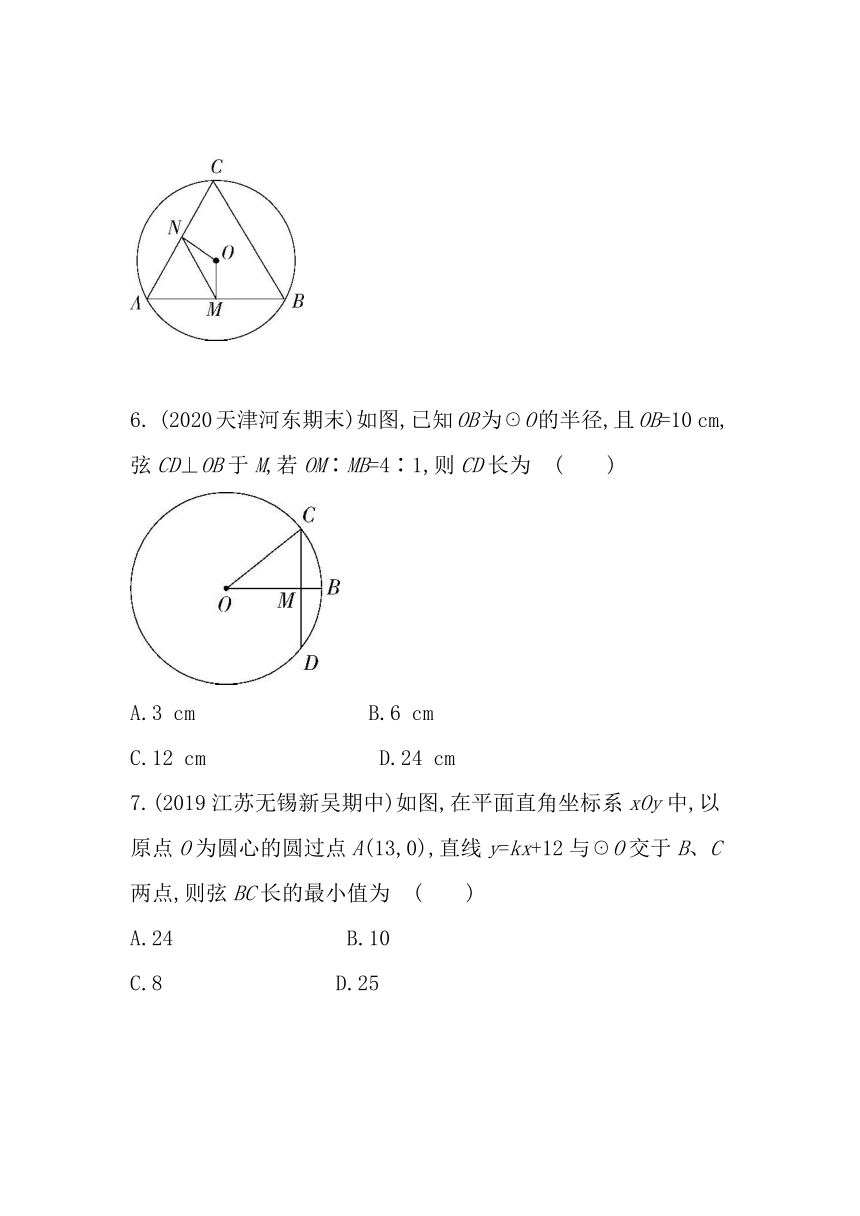
6.
(2020天津河东期末)如图,已知OB为☉O的半径,且OB=10
cm,弦CD⊥OB于M,若OM∶MB=4∶1,则CD长为?( )
A.3
cm ????B.6
cm ????
C.12
cm ????D.24
cm
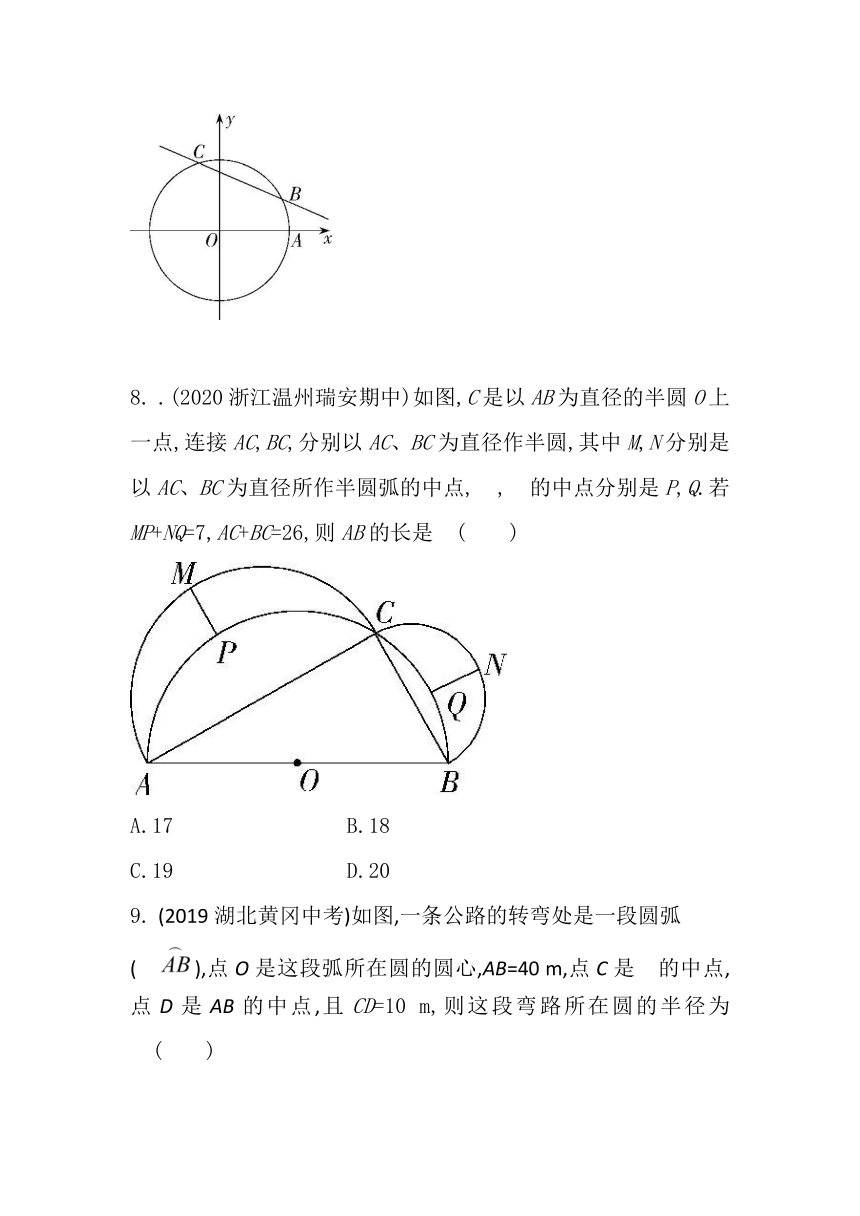
7.(2019江苏无锡新吴期中)如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx+12与☉O交于B、C两点,则弦BC长的最小值为?( )
A.24 ????B.10 ????
C.8 ????D.25
8.
.(2020浙江温州瑞安期中)如图,C是以AB为直径的半圆O上一点,连接AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是以AC、BC为直径所作半圆弧的中点,?,?的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是?( )
A.17 ????B.18 ????
C.19 ????D.20
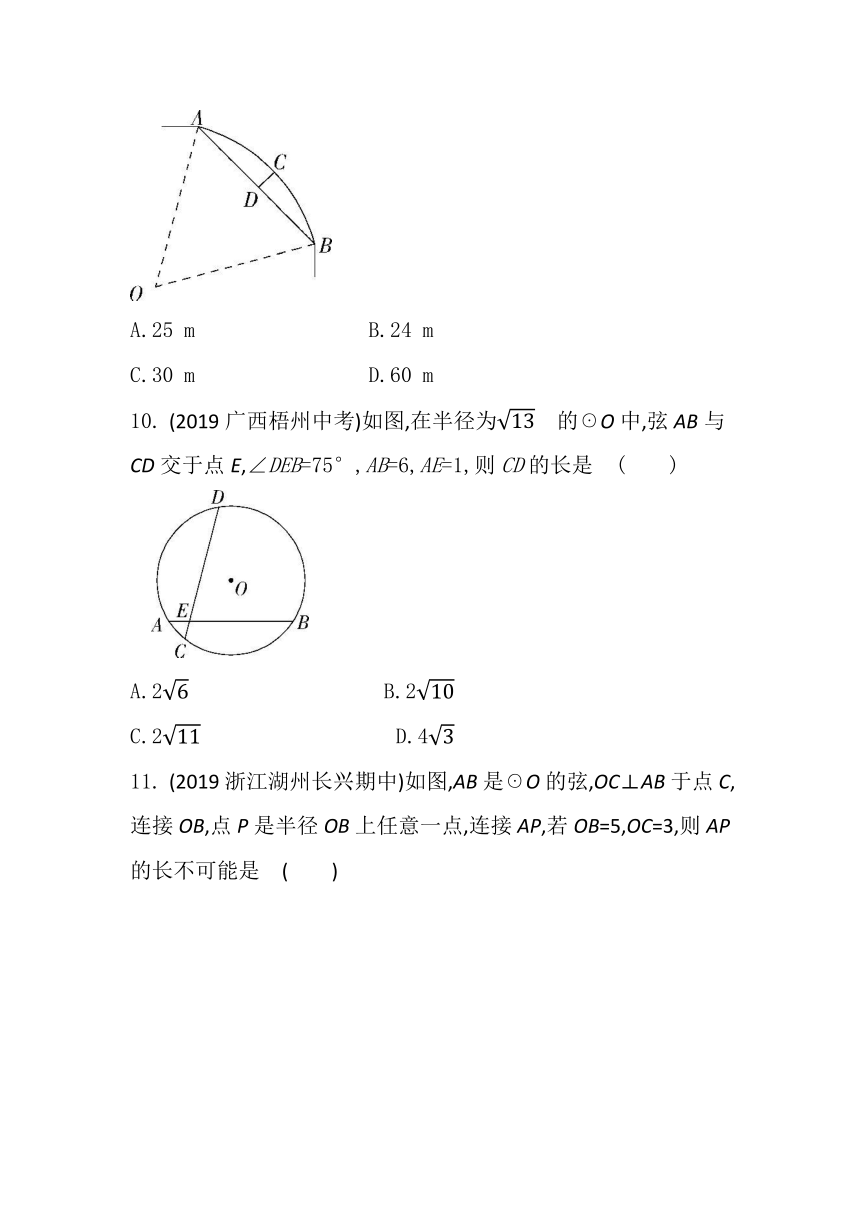
9.
(2019湖北黄冈中考)如图,一条公路的转弯处是一段圆弧
(?),点O是这段弧所在圆的圆心,AB=40
m,点C是?的中点,点D是AB的中点,且CD=10
m,则这段弯路所在圆的半径为?( )
A.25
m ????B.24
m ????
C.30
m ????D.60
m
10.
(2019广西梧州中考)如图,在半径为?的☉O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是?( )
?
A.2? ????B.2? ????
C.2? ????D.4?
11.
(2019浙江湖州长兴期中)如图,AB是☉O的弦,OC⊥AB于点C,连接OB,点P是半径OB上任意一点,连接AP,若OB=5,OC=3,则AP的长不可能是?( )
?A.6 ??B.7 ????C.8 ????D.9
12.
(2020独家原创试题)如图,AB是☉O的直径,C,D是☉O上的两动点(C,D不与A,B重合),OC⊥OD,CE⊥AB于E,DF⊥AB于F,若AB=10,则CE+DF的最大值为?( )
?
A.10 ????B.5? ????
C.5 ????D.不能确定
13.(2020浙江温州瑞安期末)如图,某公路上有一隧道,顶部是圆弧形拱顶,圆心为O,隧道的水平宽度AB为24
m,AB离地面的高度AE=10
m,拱顶最高处C离地面的高度CD为18
m,在拱顶的M,N处安装照明灯,且M,N离地面的高度相等,都等于17
m,则MN= ????m.
14.如图所示,三圆同心于O,AB=4
cm,CD⊥AB于O,则图中阴影部分的面积为 ????cm2.
15.
(2019湖北武汉东西湖期中)如图,在☉O中,AB是直径,弦AE的垂直平分线交☉O于点C,交AE于点F,CD⊥AB于D,BD=1,AE=4,则AD的长为 ????.
16.
(2020吉林白山长白期末)如图,半径为5的☉O中,AB、DE是互相垂直的两条弦,垂足为P,且AB=ED=8,则OP= ????.
17.
(2020天津河东期末)如图,已知OB为☉O的半径,且OB=10
cm,弦CD⊥OB于M,若OM∶MB=4∶1,则CD长为?( )
?
A.3
cm ????B.6
cm ????
C.12
cm ????D.24
cm
18.
(2019江苏无锡新吴期中)如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx+12与☉O交于B、C两点,则弦BC长的最小值为?( )
?A.24 ????B.10 ????
C.8 ????D.25
19.
(2019江苏无锡江阴月考)如图,
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA长为半径的圆与AB交于点D,则BD的长为 ????.
20.
(2019浙江嘉兴中考)如图,在☉O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交☉O于点D,则CD的最大值为 ????.
21.
如图,在平面直角坐标系中,以原点O为圆心的圆过点A(0,3?),直线y=kx-3k+4(k≠0)与☉O交于B,C两点,则弦BC的长的最小值为 ????.
22.
(2020甘肃白银会宁会师中学模拟)如图,CD为☉O的直径,CD⊥AB,垂足为F,直线AO⊥BC,垂足为E,BC=2?.
(1)求AB的长;
(2)求☉O的半径.
参考答案
1.
答案????D 圆既是轴对称图形,又是中心对称图形,所以A说法正确;圆是一个特殊的中心对称图形,它绕着圆心旋转任意角度都能与自身重合,所以B说法正确;圆的对称轴是过圆心的直线,这样的直线有无数条,对称中心只有一个,是圆心,所以C说法正确;直径是线段而不是直线,不能说直径是圆的对称轴,所以D说法错误.故选D.
2.
答案????C????
Rt△OAC中,OA=5,OC=3.根据勾股定理,
所以AB=2AC=8.故选C.
3.
答案????B
4.
答案????D
5.
答案????B ∵OM⊥AB,ON⊥AC,垂足分别为M,N,∴M,N分别是AB与AC的中点,∴MN是△ABC的中位线,∴BC=2MN=2,故选B.
6.
答案????C
7.
答案????B????y=kx+12,当x=0时,y=12,故直线y=kx+12恒过点(0,12),记为点D.过圆内定点D的所有弦中,与OD垂直的弦最短.如图,连接OB,∵OB=OA=13,OD=12,∴在Rt△
OBD中,BD=?=5,∴BC=2BD=10.故选B.
8.
答案????C 如图,连接OP,OQ,分别交AC,BC于H,I,∵M,N分别是以AC、BC为直径所作半圆弧的中点,
?,
?的中点分别是P,Q,∴OP⊥AC,OQ⊥BC,由对称性可知H,P,
M三点共线,I,Q,N三点共线,∴H、I是AC、BC的中点,
∴OH+OI=?(AC+BC)=13,
∵MH+NI=?AC+?BC=13,MP+NQ=7,
∴PH+QI=13-7=6,∴AB=OP+OQ=OH+OI+PH+QI=13+6=19.故选C.
9.
答案????A 连接OD,可知O、D、C三点共线,OC⊥AB,由题意知AD=DB=20
m,在Rt△AOD中,OA2=OD2+AD2,设半径为r
m,得r2=(r-10)2+202,解得r=25,∴这段弯路所在圆的半径为25
m.故选A.
10.
答案????C 如图,过点O作OF⊥CD于点F,OG⊥AB于G,连接OB、OD、OE,则DF=CF,AG=BG=?AB=3,∴EG=AG-AE=2.在Rt△BOG中,OG=?=?=2,
∴EG=OG,∴△EOG是等腰直角三角形,∴∠OEG=45°,OE=?OG=2?.
∵∠DEB=75°,∴∠OEF=30°,∴OF=?OE=?,在Rt△ODF中,DF=?=?=?,
∴CD=2DF=2?.故选C.
11.
答案????D
如图,连接OA,∵OC⊥AB于点C,OB=5,OC=3,∴BC=?=4,∴AB=2BC=2×4=8,∵AO≤AP≤AB,∴5≤AP≤8,∴AP的长度不可能是9.故选D.
12.
答案????B
∵AB=10,∴OC=OD=5.∵OC⊥OD,∴CD=?=5?.
∵OC⊥OD,CE⊥AB,DF⊥AB,
∴∠CEO=∠OFD=90°,∠COE+∠FOD=90°,∠COE+∠ECO=90°,
∴∠ECO=∠FOD.又∵OC=OD,
∴△ECO≌△FOD,
∴CE=OF,OE=DF,
∴CE+DF=OE+OF=EF.在运动过程中,EF≤CD,当CD∥EF时,EF=CD=5?,即CE+DF的最大值为5?.故选B.
13.
答案 10
如图,连接OA、OM,设CD与AB交于G,与MN交于H,∵CD=18
m,AE=10
m,AB=24
m,HD=17
m,∴CG=8
m,AG=12
m,CH=1
m.设圆拱的半径为r
m,在Rt△AOG中,OA2=OG2+AG2,∴r2=(r-8)2+122,解得r=13,∴OC=13
m,∴OH=13-1=12m.Rt△MOH中,OM2=OH2+MH2,
∴132=122+MH2,解得MH2=25,∴MH=5
m,∴MN=10
m.
14.
答案????π
?根据圆的轴对称性可将三个阴影部分的图形组合在一起,则阴影部分的面积正好等于最大圆的面积的?,即S阴影=?S最大圆=?π×(4÷2)2=π(cm2).
15.
答案 4
?∵直线CF是弦AE的垂直平分线,AE=4,
∴AF=?AE=2,∠AFO=90°.
∵CD⊥AB,∴∠ODC=∠OFA=90°.
∵OA=OC,∠AOF=∠COD,∴△AOF≌△COD(AAS),
∴CD=AF=2.设☉O的半径为r,则OD=r-1,由勾股定理得OC2=OD2+CD2,即r2=(r-1)2+22,解得r=?,
∴AD=AB-BD=2×?-1=4.
16.
答案?
3
如图,作OM⊥AB于M,ON⊥DE于N,连接OB,OD,由垂径定理、勾股定理得:OM=ON=?=3.
∵弦AB、DE互相垂直,∴∠DPB=90°.
∵OM⊥AB于M,ON⊥DE于N,
∴∠OMP=∠ONP=90°,
∴四边形MONP是矩形.
∵OM=ON,∴四边形MONP是正方形,
∴OP=?OM=3?.?
17.
答案????C
∵弦CD⊥OB于M,∴CM=DM=?CD,
∵OM∶MB=4∶1,
∴OM=?OB=8
cm,
∴CM=?=?=6(cm),
∴CD=2CM=12
cm.故选C.
18.
答案????B????
y=kx+12,当x=0时,y=12,故直线y=kx+12恒过点(0,12),记为点D.过圆内点D的所有弦中,与OD垂直的弦最短.如图,连接OB,∵OB=OA=13,OD=12,
∴在Rt△OBD中,BD=?=5,
∴BC=2BD=10.故选B.
19.
答案?????
20.
答案?????
如图,连接OD,∵CD⊥OC,∴∠DCO=90°,
∴CD=?=?
(r为圆O的半径),当OC的长最小时,CD的长最大,而OC⊥AB时,OC长最小,此时D、B两点
重合,CD=CB=?AB=?×1=?,∴CD的最大值为?.
21.
答案 4
解析 如图,连接OB,过点O作OD⊥BC于点D,∵直线y=kx-3k+4必过点(3,4),∴点D的坐标为(3,4)时,弦BC最短,此时OD=5,∵以原点O为圆心的圆过点A(0,3?),∴圆的半径为3?,∴OB=3?,∴BD=?=?=2∴弦BC的长的最小值为
4?.
22.
解析 (1)如图,连接AC,
?
∵AO⊥BC,AO过点O,
∴CE=BE,∴AB=AC.
同理,AC=BC,∵BC=2?,∴AB=BC=2.
(2)∵AB=BC=AC,
∴△ABC是等边三角形,∴∠ACB=60°.
∵AC=BC,CD⊥AB,∴∠BCD=30°,
在Rt△CEO中,∵∠BCD=30°,∴OC=2OE.
∵OE2+CE2=OC2,即OE2+(?)2=(2OE)2,
∴OE=1(舍负),
∴OC=2,即☉O的半径为2.
初中数学(人教版)九年级
上册
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
1.下列说法中,不正确的是?( )
A.圆既是轴对称图形,又是中心对称图形
B.圆绕着它的圆心旋转任意角度,都能与自身重合
C.圆的对称轴有无数条,对称中心只有一个
D.圆的每一条直径都是它的对称轴
2.
(2020江苏南通如皋中学期中)如图,在☉O中,AB为弦,OC⊥AB,垂足为点C,若OA=5,OC=3,则弦AB长为?( )
A.4 ????B.6 ????
C.8 ????D.10
3.
(2020福建福州福清期中)如图,☉O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),则OP的最小值是?( )
A.2.5 ????B.3 ????
C.3.5 ????D.4
4.
(2019山东滨州滨城模拟)如图,某下水道的横截面是圆形的,水面CD的宽度为2
m,F是线段CD的中点,EF经过圆心O交☉O于点E,EF=3
m,则☉O的直径是( )
A.?
m ????B.?
m ????
C.?
m ????D.?
m
5.
(2019湖北武汉硚口期中)如图,AB、AC、BC都是☉O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=1,则BC的值为?( )
A.1 ????B.2 ????
C.3 ????D.4
6.
(2020天津河东期末)如图,已知OB为☉O的半径,且OB=10
cm,弦CD⊥OB于M,若OM∶MB=4∶1,则CD长为?( )
A.3
cm ????B.6
cm ????
C.12
cm ????D.24
cm
7.(2019江苏无锡新吴期中)如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx+12与☉O交于B、C两点,则弦BC长的最小值为?( )
A.24 ????B.10 ????
C.8 ????D.25
8.
.(2020浙江温州瑞安期中)如图,C是以AB为直径的半圆O上一点,连接AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是以AC、BC为直径所作半圆弧的中点,?,?的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是?( )
A.17 ????B.18 ????
C.19 ????D.20
9.
(2019湖北黄冈中考)如图,一条公路的转弯处是一段圆弧
(?),点O是这段弧所在圆的圆心,AB=40
m,点C是?的中点,点D是AB的中点,且CD=10
m,则这段弯路所在圆的半径为?( )
A.25
m ????B.24
m ????
C.30
m ????D.60
m
10.
(2019广西梧州中考)如图,在半径为?的☉O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是?( )
?
A.2? ????B.2? ????
C.2? ????D.4?
11.
(2019浙江湖州长兴期中)如图,AB是☉O的弦,OC⊥AB于点C,连接OB,点P是半径OB上任意一点,连接AP,若OB=5,OC=3,则AP的长不可能是?( )
?A.6 ??B.7 ????C.8 ????D.9
12.
(2020独家原创试题)如图,AB是☉O的直径,C,D是☉O上的两动点(C,D不与A,B重合),OC⊥OD,CE⊥AB于E,DF⊥AB于F,若AB=10,则CE+DF的最大值为?( )
?
A.10 ????B.5? ????
C.5 ????D.不能确定
13.(2020浙江温州瑞安期末)如图,某公路上有一隧道,顶部是圆弧形拱顶,圆心为O,隧道的水平宽度AB为24
m,AB离地面的高度AE=10
m,拱顶最高处C离地面的高度CD为18
m,在拱顶的M,N处安装照明灯,且M,N离地面的高度相等,都等于17
m,则MN= ????m.
14.如图所示,三圆同心于O,AB=4
cm,CD⊥AB于O,则图中阴影部分的面积为 ????cm2.
15.
(2019湖北武汉东西湖期中)如图,在☉O中,AB是直径,弦AE的垂直平分线交☉O于点C,交AE于点F,CD⊥AB于D,BD=1,AE=4,则AD的长为 ????.
16.
(2020吉林白山长白期末)如图,半径为5的☉O中,AB、DE是互相垂直的两条弦,垂足为P,且AB=ED=8,则OP= ????.
17.
(2020天津河东期末)如图,已知OB为☉O的半径,且OB=10
cm,弦CD⊥OB于M,若OM∶MB=4∶1,则CD长为?( )
?
A.3
cm ????B.6
cm ????
C.12
cm ????D.24
cm
18.
(2019江苏无锡新吴期中)如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx+12与☉O交于B、C两点,则弦BC长的最小值为?( )
?A.24 ????B.10 ????
C.8 ????D.25
19.
(2019江苏无锡江阴月考)如图,
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA长为半径的圆与AB交于点D,则BD的长为 ????.
20.
(2019浙江嘉兴中考)如图,在☉O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交☉O于点D,则CD的最大值为 ????.
21.
如图,在平面直角坐标系中,以原点O为圆心的圆过点A(0,3?),直线y=kx-3k+4(k≠0)与☉O交于B,C两点,则弦BC的长的最小值为 ????.
22.
(2020甘肃白银会宁会师中学模拟)如图,CD为☉O的直径,CD⊥AB,垂足为F,直线AO⊥BC,垂足为E,BC=2?.
(1)求AB的长;
(2)求☉O的半径.
参考答案
1.
答案????D 圆既是轴对称图形,又是中心对称图形,所以A说法正确;圆是一个特殊的中心对称图形,它绕着圆心旋转任意角度都能与自身重合,所以B说法正确;圆的对称轴是过圆心的直线,这样的直线有无数条,对称中心只有一个,是圆心,所以C说法正确;直径是线段而不是直线,不能说直径是圆的对称轴,所以D说法错误.故选D.
2.
答案????C????
Rt△OAC中,OA=5,OC=3.根据勾股定理,
所以AB=2AC=8.故选C.
3.
答案????B
4.
答案????D
5.
答案????B ∵OM⊥AB,ON⊥AC,垂足分别为M,N,∴M,N分别是AB与AC的中点,∴MN是△ABC的中位线,∴BC=2MN=2,故选B.
6.
答案????C
7.
答案????B????y=kx+12,当x=0时,y=12,故直线y=kx+12恒过点(0,12),记为点D.过圆内定点D的所有弦中,与OD垂直的弦最短.如图,连接OB,∵OB=OA=13,OD=12,∴在Rt△
OBD中,BD=?=5,∴BC=2BD=10.故选B.
8.
答案????C 如图,连接OP,OQ,分别交AC,BC于H,I,∵M,N分别是以AC、BC为直径所作半圆弧的中点,
?,
?的中点分别是P,Q,∴OP⊥AC,OQ⊥BC,由对称性可知H,P,
M三点共线,I,Q,N三点共线,∴H、I是AC、BC的中点,
∴OH+OI=?(AC+BC)=13,
∵MH+NI=?AC+?BC=13,MP+NQ=7,
∴PH+QI=13-7=6,∴AB=OP+OQ=OH+OI+PH+QI=13+6=19.故选C.
9.
答案????A 连接OD,可知O、D、C三点共线,OC⊥AB,由题意知AD=DB=20
m,在Rt△AOD中,OA2=OD2+AD2,设半径为r
m,得r2=(r-10)2+202,解得r=25,∴这段弯路所在圆的半径为25
m.故选A.
10.
答案????C 如图,过点O作OF⊥CD于点F,OG⊥AB于G,连接OB、OD、OE,则DF=CF,AG=BG=?AB=3,∴EG=AG-AE=2.在Rt△BOG中,OG=?=?=2,
∴EG=OG,∴△EOG是等腰直角三角形,∴∠OEG=45°,OE=?OG=2?.
∵∠DEB=75°,∴∠OEF=30°,∴OF=?OE=?,在Rt△ODF中,DF=?=?=?,
∴CD=2DF=2?.故选C.
11.
答案????D
如图,连接OA,∵OC⊥AB于点C,OB=5,OC=3,∴BC=?=4,∴AB=2BC=2×4=8,∵AO≤AP≤AB,∴5≤AP≤8,∴AP的长度不可能是9.故选D.
12.
答案????B
∵AB=10,∴OC=OD=5.∵OC⊥OD,∴CD=?=5?.
∵OC⊥OD,CE⊥AB,DF⊥AB,
∴∠CEO=∠OFD=90°,∠COE+∠FOD=90°,∠COE+∠ECO=90°,
∴∠ECO=∠FOD.又∵OC=OD,
∴△ECO≌△FOD,
∴CE=OF,OE=DF,
∴CE+DF=OE+OF=EF.在运动过程中,EF≤CD,当CD∥EF时,EF=CD=5?,即CE+DF的最大值为5?.故选B.
13.
答案 10
如图,连接OA、OM,设CD与AB交于G,与MN交于H,∵CD=18
m,AE=10
m,AB=24
m,HD=17
m,∴CG=8
m,AG=12
m,CH=1
m.设圆拱的半径为r
m,在Rt△AOG中,OA2=OG2+AG2,∴r2=(r-8)2+122,解得r=13,∴OC=13
m,∴OH=13-1=12m.Rt△MOH中,OM2=OH2+MH2,
∴132=122+MH2,解得MH2=25,∴MH=5
m,∴MN=10
m.
14.
答案????π
?根据圆的轴对称性可将三个阴影部分的图形组合在一起,则阴影部分的面积正好等于最大圆的面积的?,即S阴影=?S最大圆=?π×(4÷2)2=π(cm2).
15.
答案 4
?∵直线CF是弦AE的垂直平分线,AE=4,
∴AF=?AE=2,∠AFO=90°.
∵CD⊥AB,∴∠ODC=∠OFA=90°.
∵OA=OC,∠AOF=∠COD,∴△AOF≌△COD(AAS),
∴CD=AF=2.设☉O的半径为r,则OD=r-1,由勾股定理得OC2=OD2+CD2,即r2=(r-1)2+22,解得r=?,
∴AD=AB-BD=2×?-1=4.
16.
答案?
3
如图,作OM⊥AB于M,ON⊥DE于N,连接OB,OD,由垂径定理、勾股定理得:OM=ON=?=3.
∵弦AB、DE互相垂直,∴∠DPB=90°.
∵OM⊥AB于M,ON⊥DE于N,
∴∠OMP=∠ONP=90°,
∴四边形MONP是矩形.
∵OM=ON,∴四边形MONP是正方形,
∴OP=?OM=3?.?
17.
答案????C
∵弦CD⊥OB于M,∴CM=DM=?CD,
∵OM∶MB=4∶1,
∴OM=?OB=8
cm,
∴CM=?=?=6(cm),
∴CD=2CM=12
cm.故选C.
18.
答案????B????
y=kx+12,当x=0时,y=12,故直线y=kx+12恒过点(0,12),记为点D.过圆内点D的所有弦中,与OD垂直的弦最短.如图,连接OB,∵OB=OA=13,OD=12,
∴在Rt△OBD中,BD=?=5,
∴BC=2BD=10.故选B.
19.
答案?????
20.
答案?????
如图,连接OD,∵CD⊥OC,∴∠DCO=90°,
∴CD=?=?
(r为圆O的半径),当OC的长最小时,CD的长最大,而OC⊥AB时,OC长最小,此时D、B两点
重合,CD=CB=?AB=?×1=?,∴CD的最大值为?.
21.
答案 4
解析 如图,连接OB,过点O作OD⊥BC于点D,∵直线y=kx-3k+4必过点(3,4),∴点D的坐标为(3,4)时,弦BC最短,此时OD=5,∵以原点O为圆心的圆过点A(0,3?),∴圆的半径为3?,∴OB=3?,∴BD=?=?=2∴弦BC的长的最小值为
4?.
22.
解析 (1)如图,连接AC,
?
∵AO⊥BC,AO过点O,
∴CE=BE,∴AB=AC.
同理,AC=BC,∵BC=2?,∴AB=BC=2.
(2)∵AB=BC=AC,
∴△ABC是等边三角形,∴∠ACB=60°.
∵AC=BC,CD⊥AB,∴∠BCD=30°,
在Rt△CEO中,∵∠BCD=30°,∴OC=2OE.
∵OE2+CE2=OC2,即OE2+(?)2=(2OE)2,
∴OE=1(舍负),
∴OC=2,即☉O的半径为2.
同课章节目录
