23.1.2平行线分线段成比例 课件(共23张PPT)
文档属性
| 名称 | 23.1.2平行线分线段成比例 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 414.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 20:23:32 | ||
图片预览



文档简介
(共23张PPT)
2.平行线分线段成比例
华东师大版
九年级数学上册
上课课件
学习目标:
了解平行线分线段成比例定理的证明,掌握定理的内容.能应用定理证明线段成比例等问题,并会进行有关的计算.
学习重点:
定理的应用.
学习难点:
定理的推导证明.
1.平行线等分线段定理
推论1
推论2
2.平行线等分线段定理的应用
把线段
n
等分.
证明同一直线上的线段相等.
复习导入
A
B
C
m
n
D
E
F
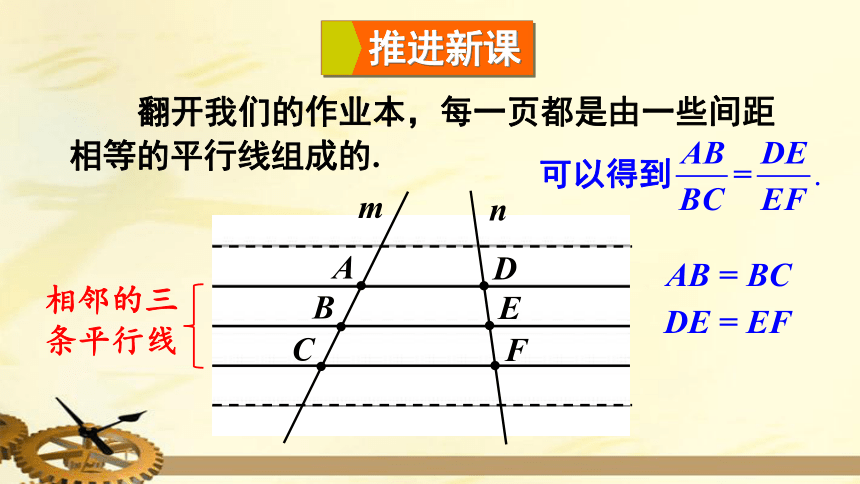
翻开我们的作业本,每一页都是由一些间距相等的平行线组成的.
推进新课
AB
=
BC
DE
=
EF
相邻的三条平行线
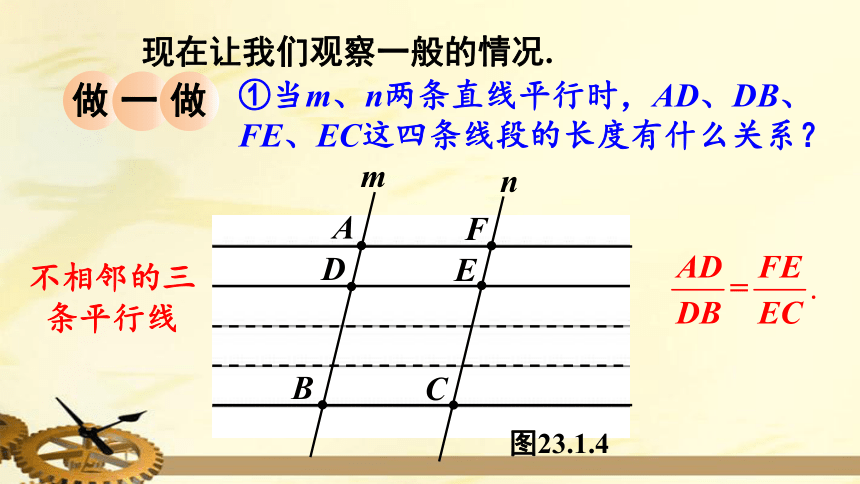
现在让我们观察一般的情况.
做
一
做
A
D
B
m
F
E
C
n
不相邻的三条平行线
①当m、n两条直线平行时,AD、DB、FE、EC这四条线段的长度有什么关系?
图23.1.4
A
D
B
m
F
E
C
n
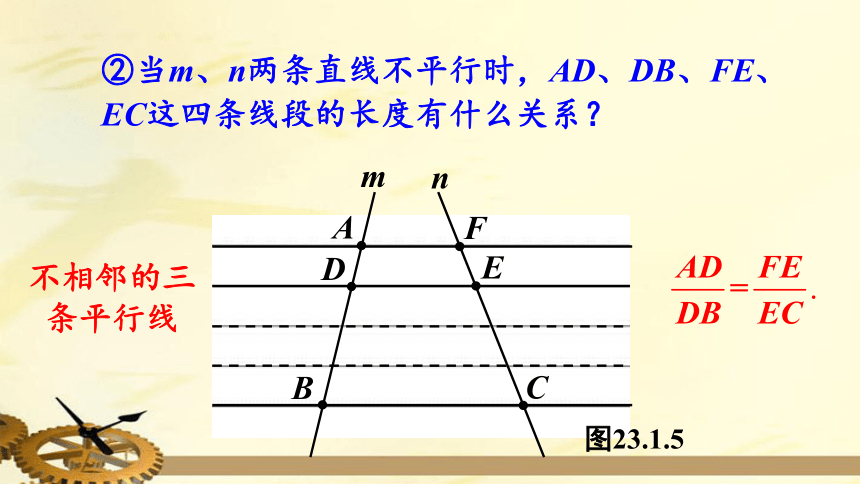
不相邻的三条平行线
②当m、n两条直线不平行时,AD、DB、FE、EC这四条线段的长度有什么关系?
图23.1.5
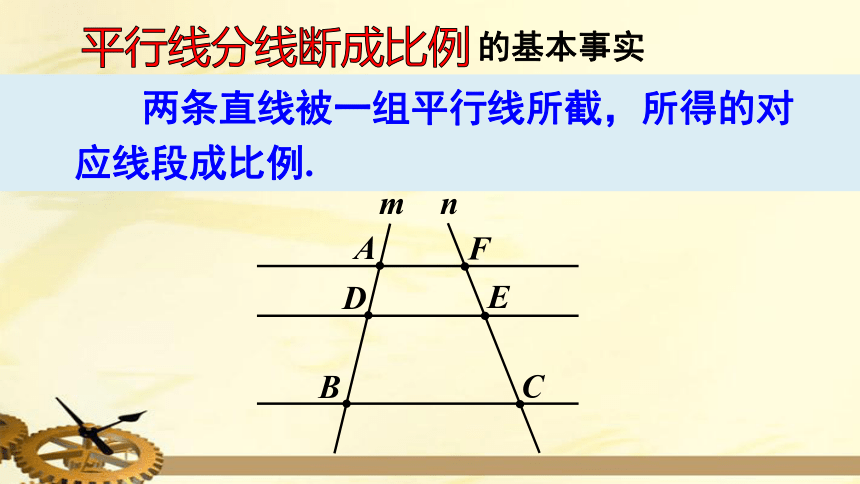
两条直线被一组平行线所截,所得的对应线段成比例.
A
D
B
m
F
E
C
n
的基本事实
平行线分线断成比例
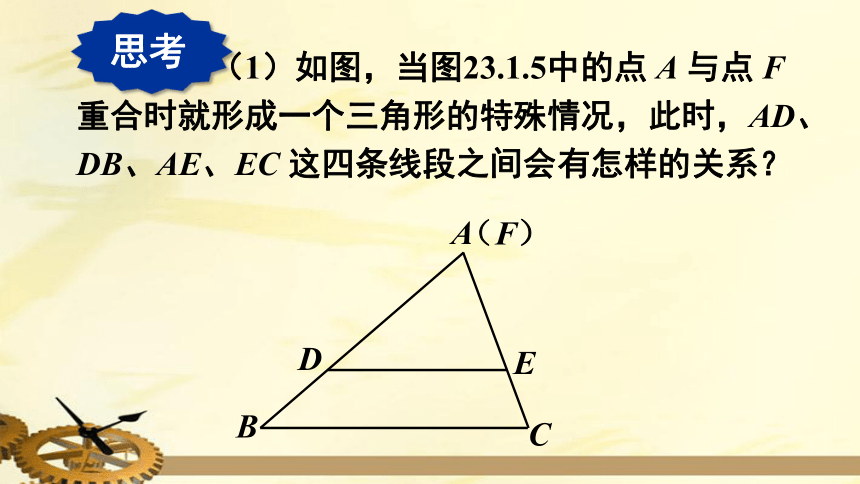
思考
(1)如图,当图23.1.5中的点
A
与点
F
重合时就形成一个三角形的特殊情况,此时,AD、DB、AE、EC
这四条线段之间会有怎样的关系?
A
D
B
(F)
E
C
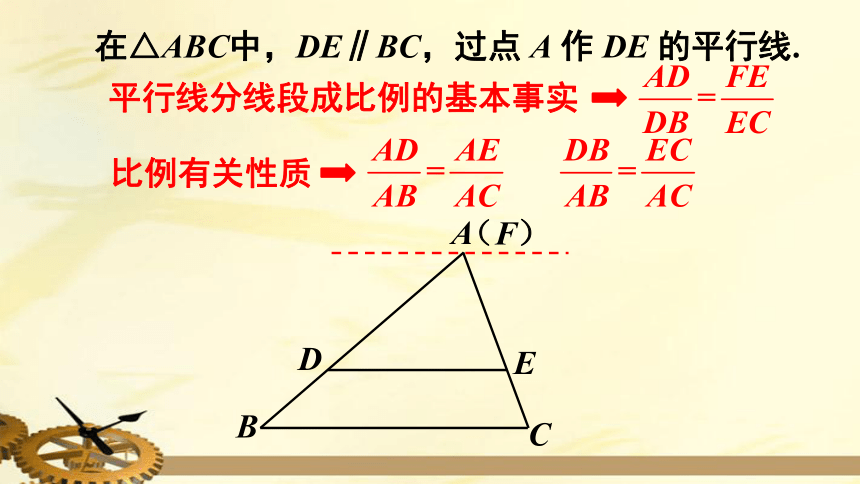
在△ABC中,DE∥BC,过点
A
作
DE
的平行线.
平行线分线段成比例的基本事实
比例有关性质
A
D
B
(F)
E
C
思考
(2)如图,当图23.1.5中的直线
m、n
相交于第二条平行上某点时,是否也有类似的成比例线段呢?
A
D
B
m
E
C
n
过点
A
作
DE
的平行线
平行线分线段成比例的基本事实
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
归纳:
A
D
B
(F)
E
C
A
D
B
m
E
C
n
如图,l1∥l2∥l3,AB
=
4,DE
=
3,EF
=
6,求
BC
的长.
例3
解
∵
l1∥l2∥l3
,
∵
AB
=
4,DE
=
3,EF
=
6,
∴
BC
=
8.
A
B
C
D
E
F
l1
l2
l3
如图,E
为□
ABCD
的边
CD
的延长线上的一点,连结
BE,交
AC
于点
O,交
AD
于点
F
.
求证:
例4
A
B
C
D
E
O
F
∵
AF∥BC
,
∵
AB
∥CE
,
A
B
C
D
E
O
F
证明
随堂演练
1.
如图,已知
l1∥l2∥l3,下列比例式中错误的是(
)
A
C
E
B
D
F
l1
l2
l3
D
2.
如图,AD∥BE∥CF,直线
l1、l2
与这三条平行线分别交于点
A、B、C
和点
D、E、F,
AB
=
4,BC
=
3,DF
=
9,求
EF
的长.
E
D
F
B
l2
A
C
l1
解
过
A、F
做直线
l3,交平行线
BE于
G点,可得
G
l3
E
D
F
B
l2
A
C
l1
G
l3
两千多年前,古希腊数学家欧多克索斯发现:将一条线段
AB
分割成长、短两条线段
AP、PB,若短段与长段的长度之比等于长段的长度与全长之
比,即
,则可得出这一比值等0.618···.
这种分割称为黄金分割,点
P
叫做线段
AB
的黄金
分割点.
黄金分割
A
P
B
自然界的黄金分割
女神维纳斯
课堂小结
两条直线被一组平行线所截,所得的对应线段成比例.
的基本事实
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
推论:
平行线分线断成比例
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本课时从学生所熟知的作业本入手,通过学生动手画图,测量、观察思考发现规律,归纳总结并加以应用,体会从特殊到一般的数学思维过程,进一步培养学生类比的数学思想.
谢谢欣赏
2.平行线分线段成比例
华东师大版
九年级数学上册
上课课件
学习目标:
了解平行线分线段成比例定理的证明,掌握定理的内容.能应用定理证明线段成比例等问题,并会进行有关的计算.
学习重点:
定理的应用.
学习难点:
定理的推导证明.
1.平行线等分线段定理
推论1
推论2
2.平行线等分线段定理的应用
把线段
n
等分.
证明同一直线上的线段相等.
复习导入
A
B
C
m
n
D
E
F
翻开我们的作业本,每一页都是由一些间距相等的平行线组成的.
推进新课
AB
=
BC
DE
=
EF
相邻的三条平行线
现在让我们观察一般的情况.
做
一
做
A
D
B
m
F
E
C
n
不相邻的三条平行线
①当m、n两条直线平行时,AD、DB、FE、EC这四条线段的长度有什么关系?
图23.1.4
A
D
B
m
F
E
C
n
不相邻的三条平行线
②当m、n两条直线不平行时,AD、DB、FE、EC这四条线段的长度有什么关系?
图23.1.5
两条直线被一组平行线所截,所得的对应线段成比例.
A
D
B
m
F
E
C
n
的基本事实
平行线分线断成比例
思考
(1)如图,当图23.1.5中的点
A
与点
F
重合时就形成一个三角形的特殊情况,此时,AD、DB、AE、EC
这四条线段之间会有怎样的关系?
A
D
B
(F)
E
C
在△ABC中,DE∥BC,过点
A
作
DE
的平行线.
平行线分线段成比例的基本事实
比例有关性质
A
D
B
(F)
E
C
思考
(2)如图,当图23.1.5中的直线
m、n
相交于第二条平行上某点时,是否也有类似的成比例线段呢?
A
D
B
m
E
C
n
过点
A
作
DE
的平行线
平行线分线段成比例的基本事实
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
归纳:
A
D
B
(F)
E
C
A
D
B
m
E
C
n
如图,l1∥l2∥l3,AB
=
4,DE
=
3,EF
=
6,求
BC
的长.
例3
解
∵
l1∥l2∥l3
,
∵
AB
=
4,DE
=
3,EF
=
6,
∴
BC
=
8.
A
B
C
D
E
F
l1
l2
l3
如图,E
为□
ABCD
的边
CD
的延长线上的一点,连结
BE,交
AC
于点
O,交
AD
于点
F
.
求证:
例4
A
B
C
D
E
O
F
∵
AF∥BC
,
∵
AB
∥CE
,
A
B
C
D
E
O
F
证明
随堂演练
1.
如图,已知
l1∥l2∥l3,下列比例式中错误的是(
)
A
C
E
B
D
F
l1
l2
l3
D
2.
如图,AD∥BE∥CF,直线
l1、l2
与这三条平行线分别交于点
A、B、C
和点
D、E、F,
AB
=
4,BC
=
3,DF
=
9,求
EF
的长.
E
D
F
B
l2
A
C
l1
解
过
A、F
做直线
l3,交平行线
BE于
G点,可得
G
l3
E
D
F
B
l2
A
C
l1
G
l3
两千多年前,古希腊数学家欧多克索斯发现:将一条线段
AB
分割成长、短两条线段
AP、PB,若短段与长段的长度之比等于长段的长度与全长之
比,即
,则可得出这一比值等0.618···.
这种分割称为黄金分割,点
P
叫做线段
AB
的黄金
分割点.
黄金分割
A
P
B
自然界的黄金分割
女神维纳斯
课堂小结
两条直线被一组平行线所截,所得的对应线段成比例.
的基本事实
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
推论:
平行线分线断成比例
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本课时从学生所熟知的作业本入手,通过学生动手画图,测量、观察思考发现规律,归纳总结并加以应用,体会从特殊到一般的数学思维过程,进一步培养学生类比的数学思想.
谢谢欣赏
