23.3.4 相似三角形的应用 课件(共21张PPT)
文档属性
| 名称 | 23.3.4 相似三角形的应用 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 536.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 20:32:23 | ||
图片预览




文档简介
(共21张PPT)
4.相似三角形的应用
华东师大版
九年级数学上册
上课课件
学习目标:
会应用相似三角形的有关性质,测量简单的物体的高度或宽度.自己设计方案测量高度,体会相似三角形在解决实际问题中的广泛应用.
学习重点:
构建相似三角形解决实际问题.
学习难点:
把实际问题抽象为数学问题,利用相似三角形来解决.
人们从很早开始,就懂得利用相似三角形的有关性质来计算那些不能直接测量的物体高度和两地距离.
新课导入
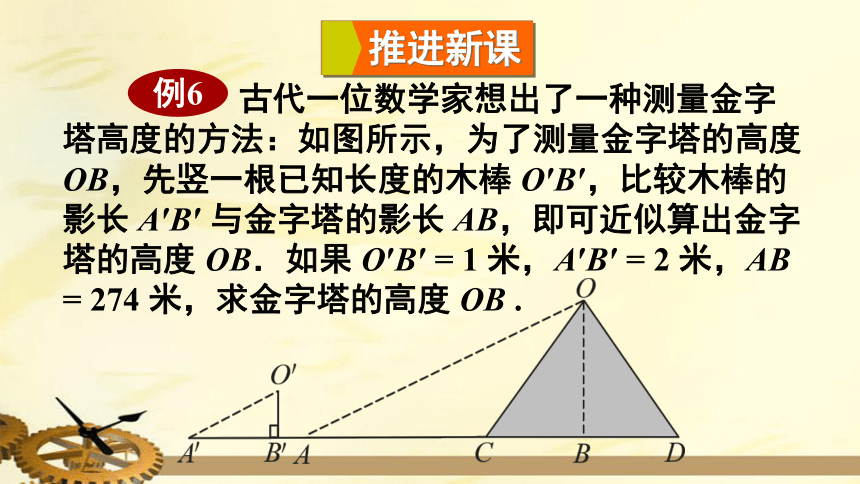
古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒
O′B′,比较木棒的影长
A′B′
与金字塔的影长
AB,即可近似算出金字塔的高度
OB.如果
O′B′
=
1
米,A′B′
=
2
米,AB
=
274
米,求金字塔的高度
OB
.
例6
推进新课
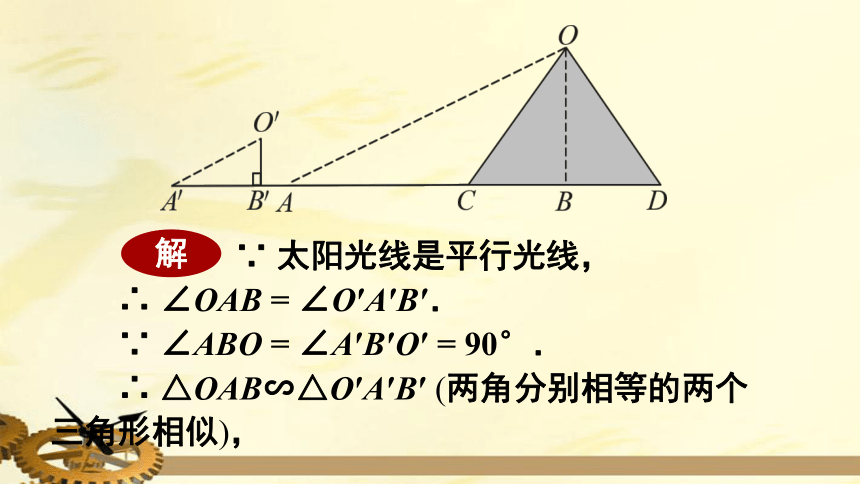
∵
太阳光线是平行光线,
∴
∠OAB
=
∠O′A′B′.
∵
∠ABO
=
∠A′B′O′
=
90°.
∴
△OAB∽△O′A′B′
(两角分别相等的两个三角形相似),
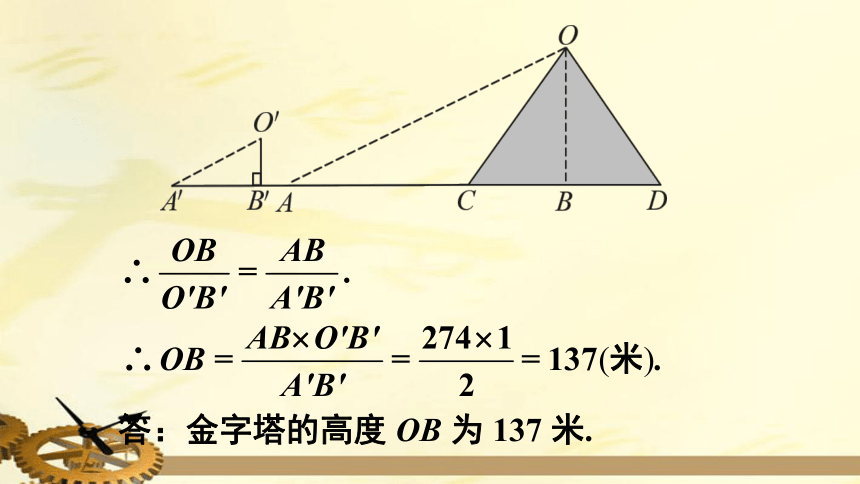
解
答:金字塔的高度
OB
为
137
米.
物1高
:物2高
=
影1长
:影2长
测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成正比例”的原理解决。
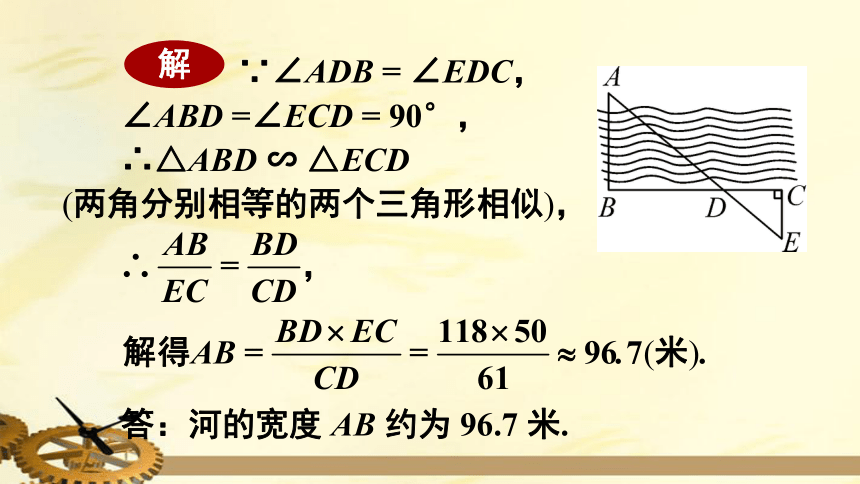
如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点
A,再在河的这一边选定点
B
和
C
,使
AB⊥BC
,然后,再选定点
E,使
EC⊥BC,用视线确定
BC
和
AE
的交点
D
.
此时如果测得
BD
=
118
米,DC
=
61
米,EC
=
50米,求河的宽度
AB.
例7
∵∠ADB
=
∠EDC,
∠ABD
=∠ECD
=
90°,
∴△ABD
∽
△ECD
(两角分别相等的两个三角形相似),
答:河的宽度
AB
约为
96.7
米.
解
另一种解法:我们还可以在河对岸选定一目标点
A,再在河的一边选点
D
和
E,使
DE⊥AD,然后,再选点
B,作
BC∥DE,与视线
EA
相交于点
C。此时,测得
DE,BC,BD,就可以求两岸间的大致距离
AB
了。
A
D
E
B
C
测距的方法
测量不能到达两点间的距离,常构造相似三角形求解。
如图,已知
D、E
分别是
△ABC
的边AB、AC
上的点,且
∠ADE
=
∠C
.
求证:AD·AB
=
AE·AC
.
例8
∵∠ADE
=
∠C,
∠A
=
∠A,
∴△ADE
∽
△ACB
(两角分别相等的两个三角形相似),
∴AD·AB
=
AE·AC.
证明
随堂演练
1.如图,一条河的两岸有一段是平行的,两岸岸边各有一排树,每排树相邻两棵的间隔都是10m,在这岸离开岸边16m处看对岸,看到对岸的两棵树的树干恰好被这岸两棵树的树干遮住,这岸的两棵树之间有一棵树,但对岸被遮住的两棵树之间有四棵树,这段河的河宽是多少米?
分析:先由实际问题建立相似的数学模型,可先证得
△ABE∽△ACD,再根据对应线段成比例可求出河宽,即线段
BC
的长.
24m
2.亮亮和颖颖住在同一幢住宅楼,两人用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰好在一条直线上时,两人分别标定自己的位置C、D,然后测出两人之间的距离CD=1.25m,颖颖与楼之间的距离DN=30m(C、D、N在一条直线上),颖颖的身高BD=1.6m,亮亮蹲地观测时眼睛到地面的距离AC=0.8m,你能根据以上测量数据帮助他们求出住宅楼的高度吗?
解:过
A
点作
AF∥CN
交
BD
于
E
点、交
MN
于
F
点,可得
BE
=
0.8m.
∵BD∥MN,∴BE∥MF,
∴△AEB
∽△AFM.
∵AE
=
CD
=
1.25m
,
AF
=
CN
=
CD
+
DN
=
31.25m,
E
F
E
F
∴
MF
=
20(m).
∴
MN
=
MF
+
FN
=
20
+
0.8
=
20.8(m).
课堂小结
解相似三角形实际问题的一般步骤:
(1)审题.
(2)构建图形.
(3)利用相似解决问题.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本节课以生活实例为情境,引导学生探究如何建立相似的数学模型,构造相似三角形,把实际问题转化为数学问题(相似)来解决,进一步提高学生应用数学知识的能力.
谢谢欣赏
4.相似三角形的应用
华东师大版
九年级数学上册
上课课件
学习目标:
会应用相似三角形的有关性质,测量简单的物体的高度或宽度.自己设计方案测量高度,体会相似三角形在解决实际问题中的广泛应用.
学习重点:
构建相似三角形解决实际问题.
学习难点:
把实际问题抽象为数学问题,利用相似三角形来解决.
人们从很早开始,就懂得利用相似三角形的有关性质来计算那些不能直接测量的物体高度和两地距离.
新课导入
古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒
O′B′,比较木棒的影长
A′B′
与金字塔的影长
AB,即可近似算出金字塔的高度
OB.如果
O′B′
=
1
米,A′B′
=
2
米,AB
=
274
米,求金字塔的高度
OB
.
例6
推进新课
∵
太阳光线是平行光线,
∴
∠OAB
=
∠O′A′B′.
∵
∠ABO
=
∠A′B′O′
=
90°.
∴
△OAB∽△O′A′B′
(两角分别相等的两个三角形相似),
解
答:金字塔的高度
OB
为
137
米.
物1高
:物2高
=
影1长
:影2长
测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成正比例”的原理解决。
如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点
A,再在河的这一边选定点
B
和
C
,使
AB⊥BC
,然后,再选定点
E,使
EC⊥BC,用视线确定
BC
和
AE
的交点
D
.
此时如果测得
BD
=
118
米,DC
=
61
米,EC
=
50米,求河的宽度
AB.
例7
∵∠ADB
=
∠EDC,
∠ABD
=∠ECD
=
90°,
∴△ABD
∽
△ECD
(两角分别相等的两个三角形相似),
答:河的宽度
AB
约为
96.7
米.
解
另一种解法:我们还可以在河对岸选定一目标点
A,再在河的一边选点
D
和
E,使
DE⊥AD,然后,再选点
B,作
BC∥DE,与视线
EA
相交于点
C。此时,测得
DE,BC,BD,就可以求两岸间的大致距离
AB
了。
A
D
E
B
C
测距的方法
测量不能到达两点间的距离,常构造相似三角形求解。
如图,已知
D、E
分别是
△ABC
的边AB、AC
上的点,且
∠ADE
=
∠C
.
求证:AD·AB
=
AE·AC
.
例8
∵∠ADE
=
∠C,
∠A
=
∠A,
∴△ADE
∽
△ACB
(两角分别相等的两个三角形相似),
∴AD·AB
=
AE·AC.
证明
随堂演练
1.如图,一条河的两岸有一段是平行的,两岸岸边各有一排树,每排树相邻两棵的间隔都是10m,在这岸离开岸边16m处看对岸,看到对岸的两棵树的树干恰好被这岸两棵树的树干遮住,这岸的两棵树之间有一棵树,但对岸被遮住的两棵树之间有四棵树,这段河的河宽是多少米?
分析:先由实际问题建立相似的数学模型,可先证得
△ABE∽△ACD,再根据对应线段成比例可求出河宽,即线段
BC
的长.
24m
2.亮亮和颖颖住在同一幢住宅楼,两人用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰好在一条直线上时,两人分别标定自己的位置C、D,然后测出两人之间的距离CD=1.25m,颖颖与楼之间的距离DN=30m(C、D、N在一条直线上),颖颖的身高BD=1.6m,亮亮蹲地观测时眼睛到地面的距离AC=0.8m,你能根据以上测量数据帮助他们求出住宅楼的高度吗?
解:过
A
点作
AF∥CN
交
BD
于
E
点、交
MN
于
F
点,可得
BE
=
0.8m.
∵BD∥MN,∴BE∥MF,
∴△AEB
∽△AFM.
∵AE
=
CD
=
1.25m
,
AF
=
CN
=
CD
+
DN
=
31.25m,
E
F
E
F
∴
MF
=
20(m).
∴
MN
=
MF
+
FN
=
20
+
0.8
=
20.8(m).
课堂小结
解相似三角形实际问题的一般步骤:
(1)审题.
(2)构建图形.
(3)利用相似解决问题.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本节课以生活实例为情境,引导学生探究如何建立相似的数学模型,构造相似三角形,把实际问题转化为数学问题(相似)来解决,进一步提高学生应用数学知识的能力.
谢谢欣赏
