23.2 相似图形 课件(共20张PPT)
文档属性
| 名称 | 23.2 相似图形 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 341.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 20:35:23 | ||
图片预览








文档简介
(共20张PPT)
23.2
相似图形
华东师大版
九年级数学上册
上课课件
学习目标:
知道相似图形的两个特征:对应边成比例,对应角相等.识别两个多边形是否相似的方法.
学习重点:
相似图形的定义和性质.
学习难点:
相似图形的性质.
我们已经知道,两个形状相同(大小可以不同)的平面图形称为相似图形.相似图形有什么主要性质?又如何判断两个图形相似与否呢?
新课导入
本节初步探索相似图形有什么主要性质.
做
一
做
AB
=
______cm,BC
=
______cm;
A'B'
=
______cm
,
B'C'
=
______cm;
∠ABC
=
______°,∠A'B'C'
=
______°.
推进新课
=
有什么关系呢?
5
2
3.5
1.4
45
45
小地图是由大地图缩小得来的,我们能感到线段A'B'、B'C'
的长度与线段
AB、BC
的长度相比,都“同样程度”地缩小了.计算可得
即AB
、A'B'、
BC
、B'C'这四条线段是成比例线段.
实际上,上面两张相似的图形中的对应线段都是成比例的,对应角都是相等的.
这样的结论对一般的相似多边形是否成立呢?
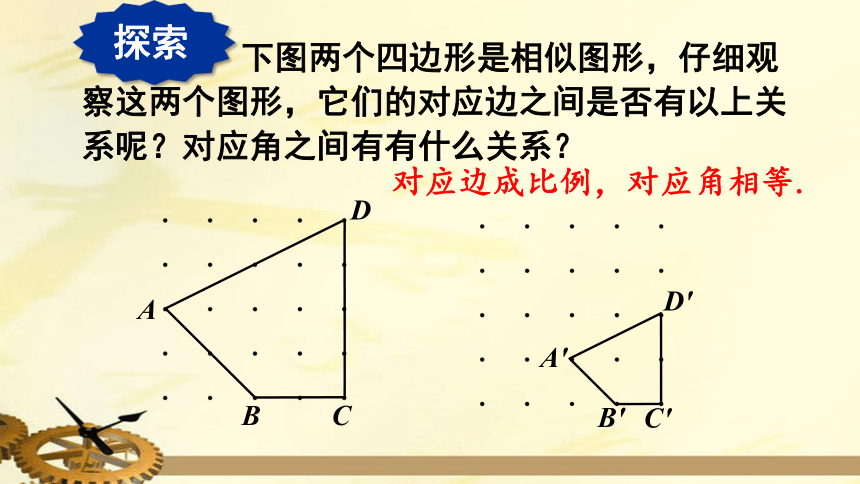
探索
下图两个四边形是相似图形,仔细观察这两个图形,它们的对应边之间是否有以上关系呢?对应角之间有有什么关系?
D
A
B
C
D'
A'
B'
C'
对应边成比例,对应角相等.
下图中两个相似的五边形,是否与你观察上图所得到的结果一样?
A
B
C
D
E
A'
B'
C'
D'
E'
对应边成比例,对应角相等.
概括
由此可以得到相似多边形的性质:
相似多边形的对应边成比例,对应角相等.
①
②
这两个特征足以刻画多边形的相似了.
在数学上我们可以给出相似多边形如下的定义:
两个边数相同的多边形,如果各边对应成比例,各角对应相等,就称这两个多边形相似.
这个定义是我们判断两个多边形是否相似的准确方法!
在下图所示的两个相似四边形中,求边
x
的长度和角
α
的大小.
例
77°
18
83°
x
α
12
18
77°
116°
解
∵两个四边形相似,
∴
x
=
27.
根据对应角相等,可得
α
=
360°-
(
77°+
83°+
116°)
=
84°.
思考
两个三角形一定是相似图形吗?两个等腰三角形呢?两个等边三角形呢?
两个三角形、两个等腰三角形不一定是相似图形.
要满足对应边成比例,对应角相等.
两个等边三角形一定是相似图形.
随堂演练
1.
矩形
ABCD
与矩形
A′B′C′D′
中,已知
AB
=
16cm,AD
=
10cm,A′D′
=
6cm,矩形
A′B′C′D′
的面积为
54cm2,这两个矩形相似吗?为什么?
解:这两个矩形不相似,由矩形A′B′C′D′的面积为
54cm2
知
A′B′
=
54÷6
=
9(cm),
2.如图,四边形
ABCD
与四边形
A′B′C′D′
是相似的,且
C′D′⊥B′C′,根据图中的条件,求出未知的边
x、y
及角
α
.
解
∵两个四边形相似,
∴
x
=
14,y
=
18.
根据对应角相等,可得
α
=
360°-
(
120°+
65°+
90°)
=
85°.
相似多边形的性质:
相似多边形的对应边成比例,对应角相等.
①
②
课堂小结
相似多边形的定义:
两个边数相同的多边形,如果各边对应成比例,各角对应相等,就称这两个多边形相似.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本节课学生通过动手测量,探究相似图形
的有关性质,经历观察、实验归纳等思维过程,从中获得数学知识与技能,体验数学活动的方
法,同时升华学生的情感、态度和价值观.
谢谢欣赏
23.2
相似图形
华东师大版
九年级数学上册
上课课件
学习目标:
知道相似图形的两个特征:对应边成比例,对应角相等.识别两个多边形是否相似的方法.
学习重点:
相似图形的定义和性质.
学习难点:
相似图形的性质.
我们已经知道,两个形状相同(大小可以不同)的平面图形称为相似图形.相似图形有什么主要性质?又如何判断两个图形相似与否呢?
新课导入
本节初步探索相似图形有什么主要性质.
做
一
做
AB
=
______cm,BC
=
______cm;
A'B'
=
______cm
,
B'C'
=
______cm;
∠ABC
=
______°,∠A'B'C'
=
______°.
推进新课
=
有什么关系呢?
5
2
3.5
1.4
45
45
小地图是由大地图缩小得来的,我们能感到线段A'B'、B'C'
的长度与线段
AB、BC
的长度相比,都“同样程度”地缩小了.计算可得
即AB
、A'B'、
BC
、B'C'这四条线段是成比例线段.
实际上,上面两张相似的图形中的对应线段都是成比例的,对应角都是相等的.
这样的结论对一般的相似多边形是否成立呢?
探索
下图两个四边形是相似图形,仔细观察这两个图形,它们的对应边之间是否有以上关系呢?对应角之间有有什么关系?
D
A
B
C
D'
A'
B'
C'
对应边成比例,对应角相等.
下图中两个相似的五边形,是否与你观察上图所得到的结果一样?
A
B
C
D
E
A'
B'
C'
D'
E'
对应边成比例,对应角相等.
概括
由此可以得到相似多边形的性质:
相似多边形的对应边成比例,对应角相等.
①
②
这两个特征足以刻画多边形的相似了.
在数学上我们可以给出相似多边形如下的定义:
两个边数相同的多边形,如果各边对应成比例,各角对应相等,就称这两个多边形相似.
这个定义是我们判断两个多边形是否相似的准确方法!
在下图所示的两个相似四边形中,求边
x
的长度和角
α
的大小.
例
77°
18
83°
x
α
12
18
77°
116°
解
∵两个四边形相似,
∴
x
=
27.
根据对应角相等,可得
α
=
360°-
(
77°+
83°+
116°)
=
84°.
思考
两个三角形一定是相似图形吗?两个等腰三角形呢?两个等边三角形呢?
两个三角形、两个等腰三角形不一定是相似图形.
要满足对应边成比例,对应角相等.
两个等边三角形一定是相似图形.
随堂演练
1.
矩形
ABCD
与矩形
A′B′C′D′
中,已知
AB
=
16cm,AD
=
10cm,A′D′
=
6cm,矩形
A′B′C′D′
的面积为
54cm2,这两个矩形相似吗?为什么?
解:这两个矩形不相似,由矩形A′B′C′D′的面积为
54cm2
知
A′B′
=
54÷6
=
9(cm),
2.如图,四边形
ABCD
与四边形
A′B′C′D′
是相似的,且
C′D′⊥B′C′,根据图中的条件,求出未知的边
x、y
及角
α
.
解
∵两个四边形相似,
∴
x
=
14,y
=
18.
根据对应角相等,可得
α
=
360°-
(
120°+
65°+
90°)
=
85°.
相似多边形的性质:
相似多边形的对应边成比例,对应角相等.
①
②
课堂小结
相似多边形的定义:
两个边数相同的多边形,如果各边对应成比例,各角对应相等,就称这两个多边形相似.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本节课学生通过动手测量,探究相似图形
的有关性质,经历观察、实验归纳等思维过程,从中获得数学知识与技能,体验数学活动的方
法,同时升华学生的情感、态度和价值观.
谢谢欣赏
