23.3.2 相似三角形的判定 第2课时 相似三角形的判定(2)课件(共24张PPT)
文档属性
| 名称 | 23.3.2 相似三角形的判定 第2课时 相似三角形的判定(2)课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 256.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 20:43:52 | ||
图片预览





文档简介
(共24张PPT)
第2课时
相似三角形的判定(2)
华东师大版
九年级数学上册
上课课件
学习目标:
1.
掌握相似三角形的判定定理2:两边成比例且夹角相等的两个三角形相似;
2.
掌握相似三角形的判定定理3:三边成比例的两个三角形相似.
3.
能依据条件,灵活应用相似三角形的判定定理,正确判断两个三角形相似.
学习重点:
相似三角形的判定定理2、3的推导过程,掌握相似三角形的判定定理2、3并能灵活应用.
学习难点:
相似三角形的判定定理的推导及应用.
现在要判断两个三角形相似有哪几种方法?
新课导入
有两种方法:(1)根据定义;(2)两角分别相等的两个三角形相似.
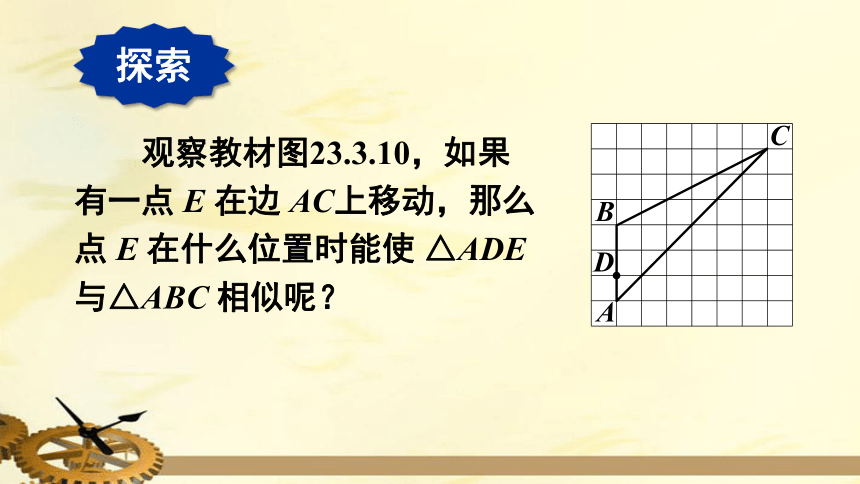
观察教材图23.3.10,如果有一点
E
在边
AC上移动,那么点
E
在什么位置时能使
△ADE
与△ABC
相似呢?
探索
A
B
C
D
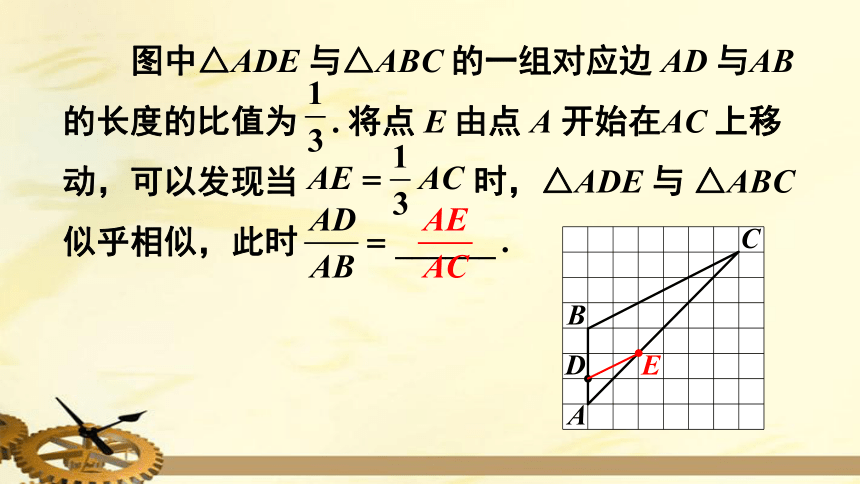
图中△ADE
与△ABC
的一组对应边
AD
与AB
的长度的比值为
.
将点
E
由点
A
开始在AC
上移动,可以发现当
时,△ADE
与
△ABC
似乎相似,此时
A
B
C
D
E
推进新课
如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.
猜想
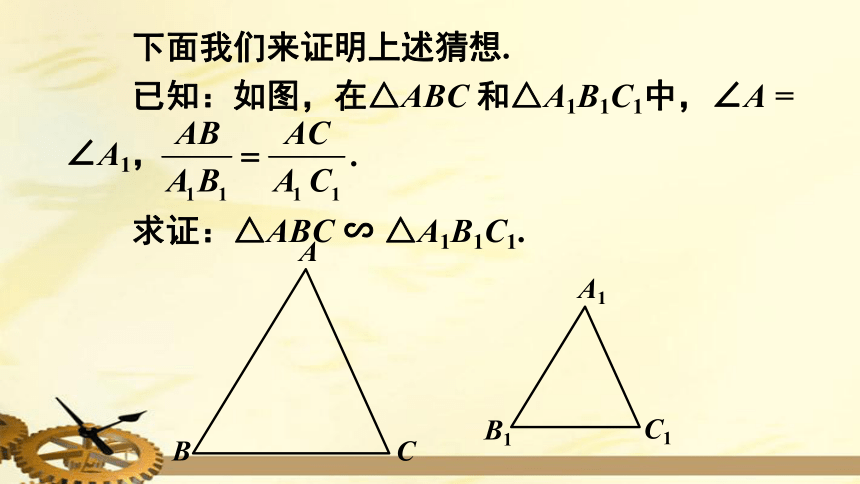
下面我们来证明上述猜想.
已知:如图,在△ABC
和△A1B1C1中,∠A
=
∠A1,
求证:△ABC
∽
△A1B1C1.
A
B
C
A1
B1
C1
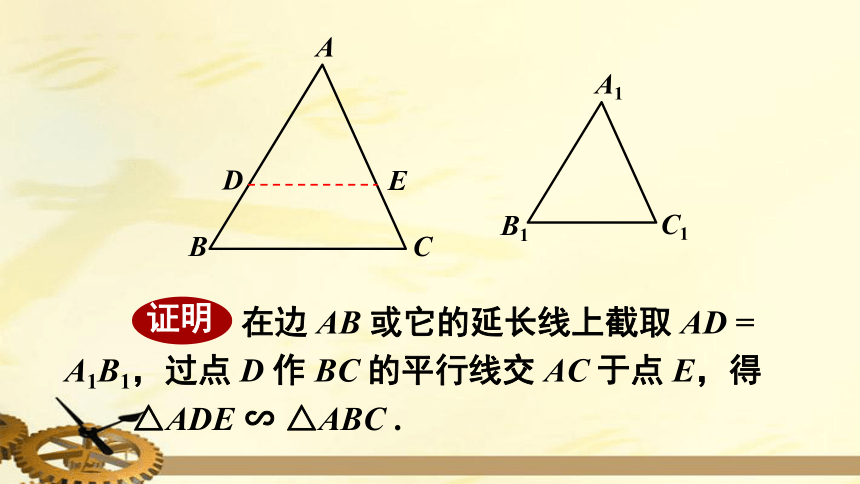
在边
AB
或它的延长线上截取
AD
=
A1B1,过点
D
作
BC
的平行线交
AC
于点
E,得
△ADE
∽
△ABC
.
证明
A
B
C
A1
B1
C1
D
E
∴
AE
=
A1C1
,
在△ADE
与△A1B1C1
中,
∵
AD
=
A1B1
,∠A
=∠A1,AE
=
A1C1
,
∴
△ADE
≌
△A1B1C1.
∴
△ABC
∽
△A1B1C1.
相似三角形的判定定理2
两边成比例且夹角相等的两个三角形相似.
判定两个三角形相似的又一个简便方法:
证明图中△AEB
和
△FEC
相似.
例4
又∵
∠AEB
=∠FEC
,
∴
△AEB
∽△FEC
(两边成比例且夹角相等的两个三角形相似).
证明
A
B
C
E
F
45
54
36
30
如果两个三角形的三条边对应成比例,那么这两个三角形相似吗?
探索
在如图所示的方格图中任画一个三角形,再画出第二个三角
形,使它的三边长都是原来三角
形三边上的相同倍数.画完之后,用量角器度量并比较两个三角形
对应角大小,你得出了什么结论?
做
一
做
相似三角形的判定定理3
三边成比例的两个三角形相似.
我们可以发现这两个三角形相似,即有如下定理:
在
△ABC
和
△A′B′C′
中,已知:AB
=
6cm,BC
=
8cm,AC
=
10cm,A′B′
=
18cm,B′C′
=
24cm,A′C′
=
30cm.试证明
△ABC
与
△A′B′C′
相似.
例5
证明
∴
△ABC
∽△A′B′C′(三边成比例的两个三角形相似).
它们的相似比是多少?
随堂演练
1.
如图,△ADE与△ABC相似吗?请说明理由.
A
B
C
D
E
2
2.5
4
5
解:△ADE与△ABC相似.
∵
∠A
=∠A,
∴
△ADE
∽
△ABC.
A
B
C
D
E
2
2.5
4
5
2.如图,已知
∠BAD
=
20°,求∠CAE
的大小.
∴
△ABC
∽
△ADE.
∴
∠BAC
=∠DAE.
又∠DAC
是公共角,
∴
∠CAE
=
∠BAD
=
20°.
A
B
C
D
E
课堂小结
相似三角形的判定定理2
两边成比例且夹角相等的两个三角形相似.
判定两个三角形相似的简便方法:
相似三角形的判定定理3
三边成比例的两个三角形相似.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本节课通过复习上节课学习的相似三角形的判定定理入手,提出新问题引入新课,再通过学生动手测量、猜想结论并证明等活动中的体验,完成对相似三角形的判定定理2、3的认识,加深对判定定理的理解.教学过程中,强调学生自主探究和合作交流,经历观察、实验、猜想、证明等思维过程,从中获得知识与技能,培养学生的综合能力.
谢谢欣赏
第2课时
相似三角形的判定(2)
华东师大版
九年级数学上册
上课课件
学习目标:
1.
掌握相似三角形的判定定理2:两边成比例且夹角相等的两个三角形相似;
2.
掌握相似三角形的判定定理3:三边成比例的两个三角形相似.
3.
能依据条件,灵活应用相似三角形的判定定理,正确判断两个三角形相似.
学习重点:
相似三角形的判定定理2、3的推导过程,掌握相似三角形的判定定理2、3并能灵活应用.
学习难点:
相似三角形的判定定理的推导及应用.
现在要判断两个三角形相似有哪几种方法?
新课导入
有两种方法:(1)根据定义;(2)两角分别相等的两个三角形相似.
观察教材图23.3.10,如果有一点
E
在边
AC上移动,那么点
E
在什么位置时能使
△ADE
与△ABC
相似呢?
探索
A
B
C
D
图中△ADE
与△ABC
的一组对应边
AD
与AB
的长度的比值为
.
将点
E
由点
A
开始在AC
上移动,可以发现当
时,△ADE
与
△ABC
似乎相似,此时
A
B
C
D
E
推进新课
如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.
猜想
下面我们来证明上述猜想.
已知:如图,在△ABC
和△A1B1C1中,∠A
=
∠A1,
求证:△ABC
∽
△A1B1C1.
A
B
C
A1
B1
C1
在边
AB
或它的延长线上截取
AD
=
A1B1,过点
D
作
BC
的平行线交
AC
于点
E,得
△ADE
∽
△ABC
.
证明
A
B
C
A1
B1
C1
D
E
∴
AE
=
A1C1
,
在△ADE
与△A1B1C1
中,
∵
AD
=
A1B1
,∠A
=∠A1,AE
=
A1C1
,
∴
△ADE
≌
△A1B1C1.
∴
△ABC
∽
△A1B1C1.
相似三角形的判定定理2
两边成比例且夹角相等的两个三角形相似.
判定两个三角形相似的又一个简便方法:
证明图中△AEB
和
△FEC
相似.
例4
又∵
∠AEB
=∠FEC
,
∴
△AEB
∽△FEC
(两边成比例且夹角相等的两个三角形相似).
证明
A
B
C
E
F
45
54
36
30
如果两个三角形的三条边对应成比例,那么这两个三角形相似吗?
探索
在如图所示的方格图中任画一个三角形,再画出第二个三角
形,使它的三边长都是原来三角
形三边上的相同倍数.画完之后,用量角器度量并比较两个三角形
对应角大小,你得出了什么结论?
做
一
做
相似三角形的判定定理3
三边成比例的两个三角形相似.
我们可以发现这两个三角形相似,即有如下定理:
在
△ABC
和
△A′B′C′
中,已知:AB
=
6cm,BC
=
8cm,AC
=
10cm,A′B′
=
18cm,B′C′
=
24cm,A′C′
=
30cm.试证明
△ABC
与
△A′B′C′
相似.
例5
证明
∴
△ABC
∽△A′B′C′(三边成比例的两个三角形相似).
它们的相似比是多少?
随堂演练
1.
如图,△ADE与△ABC相似吗?请说明理由.
A
B
C
D
E
2
2.5
4
5
解:△ADE与△ABC相似.
∵
∠A
=∠A,
∴
△ADE
∽
△ABC.
A
B
C
D
E
2
2.5
4
5
2.如图,已知
∠BAD
=
20°,求∠CAE
的大小.
∴
△ABC
∽
△ADE.
∴
∠BAC
=∠DAE.
又∠DAC
是公共角,
∴
∠CAE
=
∠BAD
=
20°.
A
B
C
D
E
课堂小结
相似三角形的判定定理2
两边成比例且夹角相等的两个三角形相似.
判定两个三角形相似的简便方法:
相似三角形的判定定理3
三边成比例的两个三角形相似.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本节课通过复习上节课学习的相似三角形的判定定理入手,提出新问题引入新课,再通过学生动手测量、猜想结论并证明等活动中的体验,完成对相似三角形的判定定理2、3的认识,加深对判定定理的理解.教学过程中,强调学生自主探究和合作交流,经历观察、实验、猜想、证明等思维过程,从中获得知识与技能,培养学生的综合能力.
谢谢欣赏
