北师大版九年级数学上册4.5相似三角形判定定理的证明 同步测试 (2)(Word版含答案)
文档属性
| 名称 | 北师大版九年级数学上册4.5相似三角形判定定理的证明 同步测试 (2)(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 152.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 08:14:54 | ||
图片预览


文档简介
北师大版九年级数学上册第四章
4.5相似三角形判定定理的证明
同步测试
一.
选择题
1.
如图,已知∠C=∠E,则不一定能使△ABC∽△ADE的条件是( )
A.∠BAD=∠CAE
B.∠B=∠D
C.
D.
2.如图,点P是ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
A.0对
B.1对
C.2对
D.3对
3.如图,下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACBB.∠ADB=∠ABCC.D.
4.下列条件中,能判定两个等腰三角形相似的是( )
A.都含有一个的内角
B.都含有一个的内角
C.都含有一个的内角
D.都含有一个的内角
5.下列两个图形:①两个等腰三角形;②两个直角三角形;③两个正方形;④两个矩形;⑤两个菱形;⑥两个正五边形.其中一定相似的有( )
A.2组
B.3组 C.4组
D.5组
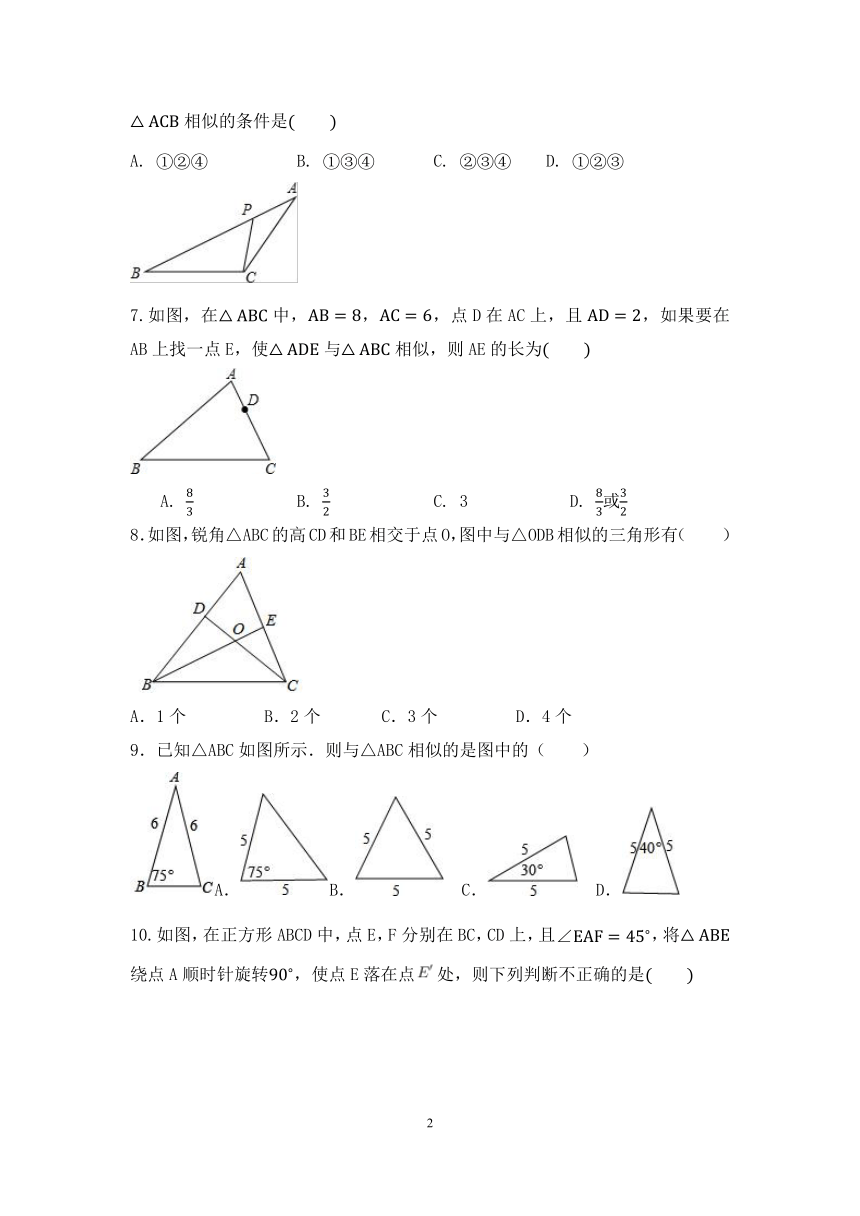
6.如图,在中,点P在边AB上,则在下列四个条件中::;;;,能满足与相似的条件是
A.
B.
C.
D.
7.如图,在中,,,点D在AC上,且,如果要在AB上找一点E,使与相似,则AE的长为
A.
B.
C.
3
D.
或
8.如图,锐角△ABC的高CD和BE相交于点O,图中与△ODB相似的三角形有( )
A.1个
B.2个
C.3个
D.4个
9.已知△ABC如图所示.则与△ABC相似的是图中的( )
A.B.
C.
D.
10.如图,在正方形ABCD中,点E,F分别在BC,CD上,且,将绕点A顺时针旋转,使点E落在点处,则下列判断不正确的是
A.
是等腰直角三角形
B.
AF垂直平分
C.
∽
D.
是等腰三角形
二.填空题
11.如图,△ABC中,AB>AC,D,E两点分别在边AC,AB上,且DE与BC不平行.请填上一个你认为合适的条件:
,使△ADE∽△ABC.(不再添加其他的字母和线段;只填一个条件,多填不给分!)
12.
已知一个三角形三边长是6cm,7.5cm,9cm,另一个三角形的三边是8cm,10cm,12cm,则这两个三角形
(填相似或不相似)
13.将一副三角板按图叠放,则△AOB与△DOC的面积之比等于
14.在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使⊿CBF∽⊿CDE,则BF的长为________
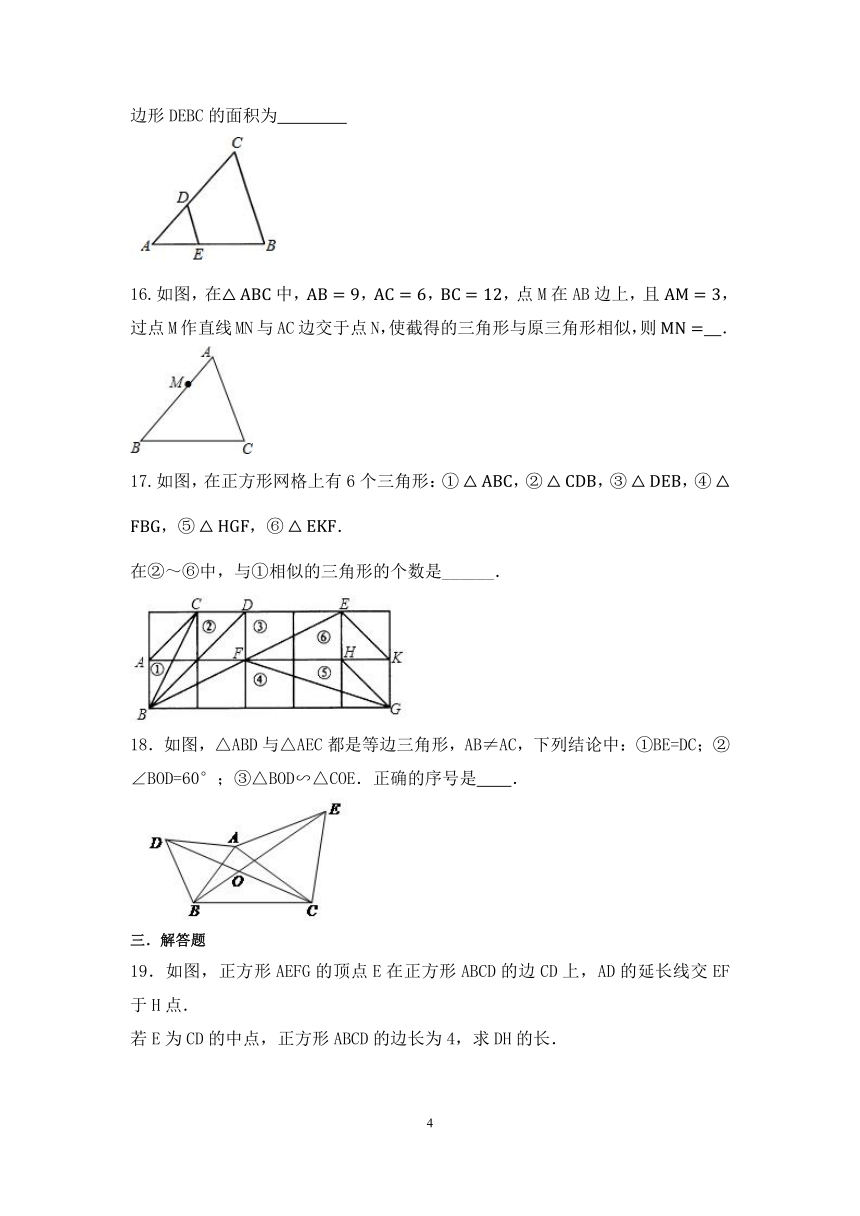
15.如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为
16.如图,在中,,,,点M在AB边上,且,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则
.
17.如图,在正方形网格上有6个三角形:,,,,,.
在中,与相似的三角形的个数是______.
18.如图,△ABD与△AEC都是等边三角形,AB≠AC,下列结论中:①BE=DC;②∠BOD=60°;③△BOD∽△COE.正确的序号是 .
三.解答题
19.如图,正方形AEFG的顶点E在正方形ABCD的边CD上,AD的延长线交EF于H点.
若E为CD的中点,正方形ABCD的边长为4,求DH的长.
20.如图,AB=3AC,BD=3AE,又BD∥AC,点B,A,E在同一条直线上.
(1)求证:△ABD∽△CAE;
(2)如果AC=BD,AD=2BD,设BD=a,求BC的长.
在图中,的内部任取一点O,连接AO、BO、CO,并在AO、BO、CO这三条线段的延长线上分别取点D、E、F,使,画出你认为与相似吗?为什么?你认为它们也具有位似形的特征吗?
22.如图,四边形ABCD中,AC平分,,,E为AB的中点.
求证:∽;
与AD有怎样的位置关系?试说明理由;
若,,求的值.
答案提示
1.D;2.D.3.D.4.C.5.A.6.D
7.
D
8.C.9.C.10.
D
11.∠C=∠2
12.相似
13.1:3.
14.
1.8
15.21.16.
4或6??17.
3??18.①②.
19.解:∵正方形AEFG和正方形ABCD中,∠AEH=∠ADC=∠EDH=,
∴∠AED+∠DEH=,∠AED+∠DAE=,
∴∠DEH=∠DAE.
∵△AED∽△EHD,
.
∵正方形ABCD的边长为4,
∴AD=CD=4.
∵E为CD的中点,
∴DE=2.
∴,
∴DH=1.
20.(1)证明:∵BD∥AC,点B,A,E在同一条直线上,
∴∠DBA=∠CAE,
又∵=3,
∴△ABD∽△CAE;
(2)连接BC,
∵AB=3AC=3BD,AD=2BD,
∴AD2+BD2=8BD2+BD2=9BD2=AB2,
∴∠D=90°,
由(1)得△ABD∽△CAE
∴∠E=∠D=90°,
∵AE=BD,EC=AD=BD,AB=3BD,
∴在Rt△BCE中,BC2=(AB+AE)2+EC2
=(3BD+BD)2+(BD)2=BD2=12a2,
∴BC=2a.
21.
解:相似如图,
,,
∽,
,
同理,
∽,
它们也具有位似形的特征.??
22.
解:平分,
,
又,
::AB,
∽;
,
理由:∽,
,
又为AB的中点,
,
,
,
,
;
,,,
,
,,
∽,
,
.??
4.5相似三角形判定定理的证明
同步测试
一.
选择题
1.
如图,已知∠C=∠E,则不一定能使△ABC∽△ADE的条件是( )
A.∠BAD=∠CAE
B.∠B=∠D
C.
D.
2.如图,点P是ABCD边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
A.0对
B.1对
C.2对
D.3对
3.如图,下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACBB.∠ADB=∠ABCC.D.
4.下列条件中,能判定两个等腰三角形相似的是( )
A.都含有一个的内角
B.都含有一个的内角
C.都含有一个的内角
D.都含有一个的内角
5.下列两个图形:①两个等腰三角形;②两个直角三角形;③两个正方形;④两个矩形;⑤两个菱形;⑥两个正五边形.其中一定相似的有( )
A.2组
B.3组 C.4组
D.5组
6.如图,在中,点P在边AB上,则在下列四个条件中::;;;,能满足与相似的条件是
A.
B.
C.
D.
7.如图,在中,,,点D在AC上,且,如果要在AB上找一点E,使与相似,则AE的长为
A.
B.
C.
3
D.
或
8.如图,锐角△ABC的高CD和BE相交于点O,图中与△ODB相似的三角形有( )
A.1个
B.2个
C.3个
D.4个
9.已知△ABC如图所示.则与△ABC相似的是图中的( )
A.B.
C.
D.
10.如图,在正方形ABCD中,点E,F分别在BC,CD上,且,将绕点A顺时针旋转,使点E落在点处,则下列判断不正确的是
A.
是等腰直角三角形
B.
AF垂直平分
C.
∽
D.
是等腰三角形
二.填空题
11.如图,△ABC中,AB>AC,D,E两点分别在边AC,AB上,且DE与BC不平行.请填上一个你认为合适的条件:
,使△ADE∽△ABC.(不再添加其他的字母和线段;只填一个条件,多填不给分!)
12.
已知一个三角形三边长是6cm,7.5cm,9cm,另一个三角形的三边是8cm,10cm,12cm,则这两个三角形
(填相似或不相似)
13.将一副三角板按图叠放,则△AOB与△DOC的面积之比等于
14.在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使⊿CBF∽⊿CDE,则BF的长为________
15.如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为
16.如图,在中,,,,点M在AB边上,且,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则
.
17.如图,在正方形网格上有6个三角形:,,,,,.
在中,与相似的三角形的个数是______.
18.如图,△ABD与△AEC都是等边三角形,AB≠AC,下列结论中:①BE=DC;②∠BOD=60°;③△BOD∽△COE.正确的序号是 .
三.解答题
19.如图,正方形AEFG的顶点E在正方形ABCD的边CD上,AD的延长线交EF于H点.
若E为CD的中点,正方形ABCD的边长为4,求DH的长.
20.如图,AB=3AC,BD=3AE,又BD∥AC,点B,A,E在同一条直线上.
(1)求证:△ABD∽△CAE;
(2)如果AC=BD,AD=2BD,设BD=a,求BC的长.
在图中,的内部任取一点O,连接AO、BO、CO,并在AO、BO、CO这三条线段的延长线上分别取点D、E、F,使,画出你认为与相似吗?为什么?你认为它们也具有位似形的特征吗?
22.如图,四边形ABCD中,AC平分,,,E为AB的中点.
求证:∽;
与AD有怎样的位置关系?试说明理由;
若,,求的值.
答案提示
1.D;2.D.3.D.4.C.5.A.6.D
7.
D
8.C.9.C.10.
D
11.∠C=∠2
12.相似
13.1:3.
14.
1.8
15.21.16.
4或6??17.
3??18.①②.
19.解:∵正方形AEFG和正方形ABCD中,∠AEH=∠ADC=∠EDH=,
∴∠AED+∠DEH=,∠AED+∠DAE=,
∴∠DEH=∠DAE.
∵△AED∽△EHD,
.
∵正方形ABCD的边长为4,
∴AD=CD=4.
∵E为CD的中点,
∴DE=2.
∴,
∴DH=1.
20.(1)证明:∵BD∥AC,点B,A,E在同一条直线上,
∴∠DBA=∠CAE,
又∵=3,
∴△ABD∽△CAE;
(2)连接BC,
∵AB=3AC=3BD,AD=2BD,
∴AD2+BD2=8BD2+BD2=9BD2=AB2,
∴∠D=90°,
由(1)得△ABD∽△CAE
∴∠E=∠D=90°,
∵AE=BD,EC=AD=BD,AB=3BD,
∴在Rt△BCE中,BC2=(AB+AE)2+EC2
=(3BD+BD)2+(BD)2=BD2=12a2,
∴BC=2a.
21.
解:相似如图,
,,
∽,
,
同理,
∽,
它们也具有位似形的特征.??
22.
解:平分,
,
又,
::AB,
∽;
,
理由:∽,
,
又为AB的中点,
,
,
,
,
;
,,,
,
,,
∽,
,
.??
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
