苏科版七年级数学上册 第3章 代数式 单元检测试题(Word版 含解析)
文档属性
| 名称 | 苏科版七年级数学上册 第3章 代数式 单元检测试题(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 65.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 10:50:46 | ||
图片预览




文档简介
第3章
代数式
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
下列各式中,符合代数式书写规则的是(
)
A.
B.
C.
D.
?
2.
关于单项式:,下列说法正确的是(
)
A.次数是
B.次数是
C.系数是
D.系数是
?
3.
填在下面各正方形中的四个数之间都有一定的规律,按此规律得出,的值分别为(
)
A.,
B.,
C.,
D.,
?
4.
某单位去年收入元,支出元,而今年收入比去年高,支出比去年低,则今年结余(
)
A.元
B.元
C.元
D.元
?5.
下列计算正确的是(?
?
?
?
)
A.
B.
C.
D.
?
6.
下列式子:,,,,,中,整式的个数有(
)
A.
B.
C.
D.
?
7.
下列结论中,正确的是(
)
A.单项式的系数是,次数是
B.单项式的次数是,没有系数
C.单项式的系数是,次数是
D.多项式是四次三项式
?
8.
对于式子:①;②;③;④;⑤.下列判断正确的是(
)
A.①③是单项式
B.②是二次三项式
C.②④是多项式
D.①⑤是整式
?
9.
下列运算错误的是(????????)
A.
B.
C.
D.
?
10.
下列去括号正确的是(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
11.
已知和是同类项,则________.
?
12.
化简:________,________.
?
13.
若抛物线
与轴的一个交点为
,则代数式
的值为________.
?
14.
去括号应得________.
?
15.
若关于,的多项式中不含有项,则________.
?
16.
一个多项式加上再减去等于,则这个多项式是________.
?
17.
若与是同类项,那么的值为________.
?
18.
已知两个多项式的和是:,其中一个多项式是:,则另一个多项式是:________.
?
19.
若,,则的值为________.
?
20.
某种商品千克的售价是元,则这种商品千克的售价是________元.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
多项式的次数和单项式的次数相同,求的值.
?
22.
先化简,再求值:求的值,其中.
?
23.
某工厂储存了天用的煤,要使储存的煤比预定的时间多用天,每天应节约用煤多少吨?
?
24.
多项式是关于的二次三项式,求与的相反数.
?
25.
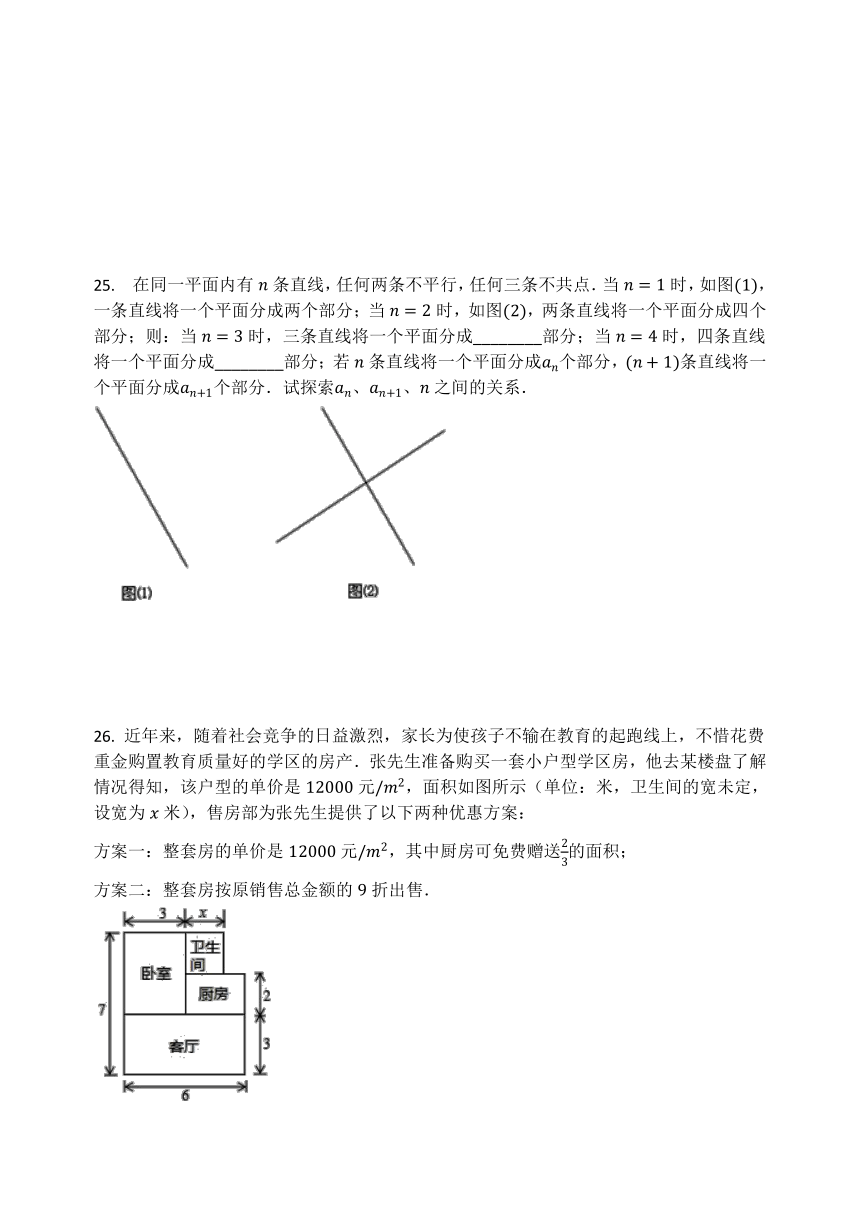
在同一平面内有条直线,任何两条不平行,任何三条不共点.当时,如图,一条直线将一个平面分成两个部分;当时,如图,两条直线将一个平面分成四个部分;则:当时,三条直线将一个平面分成________部分;当时,四条直线将一个平面分成________部分;若条直线将一个平面分成个部分,条直线将一个平面分成个部分.试探索、、之间的关系.
?
26.
近年来,随着社会竞争的日益激烈,家长为使孩子不输在教育的起跑线上,不惜花费重金购置教育质量好的学区的房产.张先生准备购买一套小户型学区房,他去某楼盘了解情况得知,该户型的单价是元,面积如图所示(单位:米,卫生间的宽未定,设宽为米),售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是元,其中厨房可免费赠送的面积;
方案二:整套房按原销售总金额的折出售.
用表示方案一中购买一套该户型商品房的总金额,用表示方案二中购买一套该户型商品房的总金额,分别求出两种方案中的总金额,(用含的式子表示);
求当时,两种方案的总金额分别是多少元?
张先生因现金不够,在银行借了万元住房贷款,贷款期限为年,从开始贷款的下一个月起逐月偿还,贷款月利率是,每月还款数额平均每月应还的贷款本金数额+月利息,月利息上月所剩贷款本金数额月利率.
①张先生借款后第一个月应还款数额是多少元?
②假设贷款月利率不变,若张先生在借款后第(,是正整数)个月的还款数额为,请写出与之间的关系式.
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【解析】
根据代数式的书写要求判断各项.
【解答】
、不符合代数式书写规则,应该为:,故此选项不合题意.
、符合代数式书写规则,故此选项符合题意;
、不符合代数式书写规则,应该为:,故此选项不合题意;
、?不符合代数式书写规则,应该为:?,故此选项不合题意;
2.
【解析】
利用单项式系数与次数的定义求解即可.
【解答】
解:单项式的系数为,次数为,
故选:.
3.
【解析】
分析前三个正方形,发现“右上的数左上的数,左下的数左上的数,右下的数右上的数右下的数”,依此即可得出、、的值.
【解答】
解:分析正方形中的四个数:
∵
第一个正方形中,,;第二个正方形中,,;第三个正方形中,,.
∴
,,.
故选.
4.
【解析】
根据题意可以列出相应的代数式,从而可以解答本题.
【解答】
解:由题意可得,今年的收入为,今年的支出为,
所以今年的结余为:(元),
故选
5.
【解析】
此题暂无解析
【解答】
解:,故错误;
,故错误;
,故正确;
与不是同类项,不能合并,故错误.
故选.
6.
【解析】
根据分母中不含有字母的式子是整式,可得答案.
【解答】
解:,,,,是整式.
故选.
7.
【解析】
根据单项式的系数及次数的定义,以及多项式的次数、系数的定义解答.
【解答】
解:解:、单项式的系数是,次数是,故选项错误;
、单项式的次数是,系数是,故选项错误;
、单项式的系数是,次数是正确的;
、多项式是二次三项式,故选项错误.
故选.
8.
【解析】
根据单项式、多项式、整式、分式的定义逐个判断即可.
【解答】
解:、①是单项式,③不是整式,也不是单项式,故本选项错误;
、②不是整式,不能说几次几项式,故本选项错误;
、②和都不是整式,也不是多项式,故本选项错误;
、是单项式,也是整式,是整式,故本选项正确;
故选.
9.
【解析】
直接利用积的乘方运算法则以及同底数幂的乘法运算、合并同类项,正确掌握相关运算法则分别化简得出答案.
【解答】
解:.,原式计算错误,故符合题意;
.,正确,故不合题意;
.,正确,故不合题意;
.,正确,故不合题意.
故选.
10.
【解析】
根据去括号法则对四个选项逐一进行分析,要注意括号前面的符号,以选用合适的法则.
【解答】
解:、,故本选项错误;
、,故本选项正确;
、,故本选项错误;
、,故本选项错误;
故选:.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【解析】
根据同类项定义得出,,求出的值后代入求出即可.
【解答】
解:∵
和是同类项,
∴
,,
∴
,
∴
,
故答案为:.
12.
【解析】
此题根据同类项定义进行计算,把同类项的系数相加.
【解答】
解:.
,
,
.
故答案分别为:,.
13.
【解析】
把点代入函数解析式,得出,再用整体代入法,即可求出代数式的值.
【解答】
解:把代入??,
得:,
则,
则.
故答案为:.
14.
【解析】
根据去括号的方法,先去中括号,再去小括号.
【解答】
解:根据去括号的方法可知:.
15.
【解析】
可以先将原多项式合并同类项,然后根据不含有项可以得到关于的方程,解方程即可解答.
【解答】
解:原式
,
由于多项式中不含有项,
故,
∴
,
故答案为:.
16.
【解析】
根据题意列出关系式,去括号合并即可得到结果.
【解答】
解:根据题意列得:
,
则这个多项式为.
故答案为:.
17.
【解析】
根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程,,求出,的值,再代入代数式计算即可.
【解答】
解:∵
与是同类项,
∴
,,
∴
,,
当时,原式;
当时,原式;
故答案为或.
18.
【解析】
根据和减去一个加数等于另一个加数,计算即可得到结果.
【解答】
解:根据题意得:,
故答案为:
19.
【解析】
已知两等式左右两边相减求出所求式子的值即可.
【解答】
解:∵
,,
∴
原式.
故答案为:.
20.
【解析】
先求出千克商品的价格,再乘以,即可解答.
【解答】
根据题意,得:,
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【解析】
根据多项式的次数的定义即可求解.
【解答】
解:单项式的次数是,则多项式的次数是,
故,
解得:.
22.
【解析】
首先去括号,然后合并同类项,化简后,代入的值求值即可.
【解答】
原式=
,
当时,原式==.
23.
【解析】
先列出实际每天用煤的重量和计划每天用煤的重量,然后求差便可.
【解答】
根据题意得,
24.
【解析】
根据多项式的次数与项数,可得、的值,根据只有符号不同的两个数互为相反数,可得与的相反数.
【解答】
解:由多项式是关于的二次三项式,得
,,
的相反数是,的相反数是.
25.
【解析】
一条直线可以把平面分成两部分,两条直线最多可以把平面分成部分,三条直线最多可以把平面分成部分,四条直线最多可以把平面分成部分,可以发现,两条直线时多了部分,三条直线比原来多了部分,四条直线时比原来多了部分,…,条时比原来多了部分.
【解答】
解:如图所示,
当时,分成部分,
当时,分成部分,
当时,分成部分,…
当时,分成部分,…
规律发现,有几条线段,则分成的部分比前一种情况多几部分,
、、之间的关系是:.
故答案为:;;.
26.
【解析】
(1)根据图中线段长度,即可表示出各部分面积,进而得出两种购买方案;
(2)利用两关系式直接得出答案;
(3)①根据贷款数以及利率即可得出张先生借款后第一个月应还款数额;
②可以得出还款数额为,进而得出即可.
【解答】
解:
,
;
当时,(元);
(元);
故当时,两种方案的金额均为元.
①(元),(元).
故张先生借款后第一个月应还元.???????????
②
代数式
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
下列各式中,符合代数式书写规则的是(
)
A.
B.
C.
D.
?
2.
关于单项式:,下列说法正确的是(
)
A.次数是
B.次数是
C.系数是
D.系数是
?
3.
填在下面各正方形中的四个数之间都有一定的规律,按此规律得出,的值分别为(
)
A.,
B.,
C.,
D.,
?
4.
某单位去年收入元,支出元,而今年收入比去年高,支出比去年低,则今年结余(
)
A.元
B.元
C.元
D.元
?5.
下列计算正确的是(?
?
?
?
)
A.
B.
C.
D.
?
6.
下列式子:,,,,,中,整式的个数有(
)
A.
B.
C.
D.
?
7.
下列结论中,正确的是(
)
A.单项式的系数是,次数是
B.单项式的次数是,没有系数
C.单项式的系数是,次数是
D.多项式是四次三项式
?
8.
对于式子:①;②;③;④;⑤.下列判断正确的是(
)
A.①③是单项式
B.②是二次三项式
C.②④是多项式
D.①⑤是整式
?
9.
下列运算错误的是(????????)
A.
B.
C.
D.
?
10.
下列去括号正确的是(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
11.
已知和是同类项,则________.
?
12.
化简:________,________.
?
13.
若抛物线
与轴的一个交点为
,则代数式
的值为________.
?
14.
去括号应得________.
?
15.
若关于,的多项式中不含有项,则________.
?
16.
一个多项式加上再减去等于,则这个多项式是________.
?
17.
若与是同类项,那么的值为________.
?
18.
已知两个多项式的和是:,其中一个多项式是:,则另一个多项式是:________.
?
19.
若,,则的值为________.
?
20.
某种商品千克的售价是元,则这种商品千克的售价是________元.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
多项式的次数和单项式的次数相同,求的值.
?
22.
先化简,再求值:求的值,其中.
?
23.
某工厂储存了天用的煤,要使储存的煤比预定的时间多用天,每天应节约用煤多少吨?
?
24.
多项式是关于的二次三项式,求与的相反数.
?
25.
在同一平面内有条直线,任何两条不平行,任何三条不共点.当时,如图,一条直线将一个平面分成两个部分;当时,如图,两条直线将一个平面分成四个部分;则:当时,三条直线将一个平面分成________部分;当时,四条直线将一个平面分成________部分;若条直线将一个平面分成个部分,条直线将一个平面分成个部分.试探索、、之间的关系.
?
26.
近年来,随着社会竞争的日益激烈,家长为使孩子不输在教育的起跑线上,不惜花费重金购置教育质量好的学区的房产.张先生准备购买一套小户型学区房,他去某楼盘了解情况得知,该户型的单价是元,面积如图所示(单位:米,卫生间的宽未定,设宽为米),售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是元,其中厨房可免费赠送的面积;
方案二:整套房按原销售总金额的折出售.
用表示方案一中购买一套该户型商品房的总金额,用表示方案二中购买一套该户型商品房的总金额,分别求出两种方案中的总金额,(用含的式子表示);
求当时,两种方案的总金额分别是多少元?
张先生因现金不够,在银行借了万元住房贷款,贷款期限为年,从开始贷款的下一个月起逐月偿还,贷款月利率是,每月还款数额平均每月应还的贷款本金数额+月利息,月利息上月所剩贷款本金数额月利率.
①张先生借款后第一个月应还款数额是多少元?
②假设贷款月利率不变,若张先生在借款后第(,是正整数)个月的还款数额为,请写出与之间的关系式.
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【解析】
根据代数式的书写要求判断各项.
【解答】
、不符合代数式书写规则,应该为:,故此选项不合题意.
、符合代数式书写规则,故此选项符合题意;
、不符合代数式书写规则,应该为:,故此选项不合题意;
、?不符合代数式书写规则,应该为:?,故此选项不合题意;
2.
【解析】
利用单项式系数与次数的定义求解即可.
【解答】
解:单项式的系数为,次数为,
故选:.
3.
【解析】
分析前三个正方形,发现“右上的数左上的数,左下的数左上的数,右下的数右上的数右下的数”,依此即可得出、、的值.
【解答】
解:分析正方形中的四个数:
∵
第一个正方形中,,;第二个正方形中,,;第三个正方形中,,.
∴
,,.
故选.
4.
【解析】
根据题意可以列出相应的代数式,从而可以解答本题.
【解答】
解:由题意可得,今年的收入为,今年的支出为,
所以今年的结余为:(元),
故选
5.
【解析】
此题暂无解析
【解答】
解:,故错误;
,故错误;
,故正确;
与不是同类项,不能合并,故错误.
故选.
6.
【解析】
根据分母中不含有字母的式子是整式,可得答案.
【解答】
解:,,,,是整式.
故选.
7.
【解析】
根据单项式的系数及次数的定义,以及多项式的次数、系数的定义解答.
【解答】
解:解:、单项式的系数是,次数是,故选项错误;
、单项式的次数是,系数是,故选项错误;
、单项式的系数是,次数是正确的;
、多项式是二次三项式,故选项错误.
故选.
8.
【解析】
根据单项式、多项式、整式、分式的定义逐个判断即可.
【解答】
解:、①是单项式,③不是整式,也不是单项式,故本选项错误;
、②不是整式,不能说几次几项式,故本选项错误;
、②和都不是整式,也不是多项式,故本选项错误;
、是单项式,也是整式,是整式,故本选项正确;
故选.
9.
【解析】
直接利用积的乘方运算法则以及同底数幂的乘法运算、合并同类项,正确掌握相关运算法则分别化简得出答案.
【解答】
解:.,原式计算错误,故符合题意;
.,正确,故不合题意;
.,正确,故不合题意;
.,正确,故不合题意.
故选.
10.
【解析】
根据去括号法则对四个选项逐一进行分析,要注意括号前面的符号,以选用合适的法则.
【解答】
解:、,故本选项错误;
、,故本选项正确;
、,故本选项错误;
、,故本选项错误;
故选:.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【解析】
根据同类项定义得出,,求出的值后代入求出即可.
【解答】
解:∵
和是同类项,
∴
,,
∴
,
∴
,
故答案为:.
12.
【解析】
此题根据同类项定义进行计算,把同类项的系数相加.
【解答】
解:.
,
,
.
故答案分别为:,.
13.
【解析】
把点代入函数解析式,得出,再用整体代入法,即可求出代数式的值.
【解答】
解:把代入??,
得:,
则,
则.
故答案为:.
14.
【解析】
根据去括号的方法,先去中括号,再去小括号.
【解答】
解:根据去括号的方法可知:.
15.
【解析】
可以先将原多项式合并同类项,然后根据不含有项可以得到关于的方程,解方程即可解答.
【解答】
解:原式
,
由于多项式中不含有项,
故,
∴
,
故答案为:.
16.
【解析】
根据题意列出关系式,去括号合并即可得到结果.
【解答】
解:根据题意列得:
,
则这个多项式为.
故答案为:.
17.
【解析】
根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程,,求出,的值,再代入代数式计算即可.
【解答】
解:∵
与是同类项,
∴
,,
∴
,,
当时,原式;
当时,原式;
故答案为或.
18.
【解析】
根据和减去一个加数等于另一个加数,计算即可得到结果.
【解答】
解:根据题意得:,
故答案为:
19.
【解析】
已知两等式左右两边相减求出所求式子的值即可.
【解答】
解:∵
,,
∴
原式.
故答案为:.
20.
【解析】
先求出千克商品的价格,再乘以,即可解答.
【解答】
根据题意,得:,
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【解析】
根据多项式的次数的定义即可求解.
【解答】
解:单项式的次数是,则多项式的次数是,
故,
解得:.
22.
【解析】
首先去括号,然后合并同类项,化简后,代入的值求值即可.
【解答】
原式=
,
当时,原式==.
23.
【解析】
先列出实际每天用煤的重量和计划每天用煤的重量,然后求差便可.
【解答】
根据题意得,
24.
【解析】
根据多项式的次数与项数,可得、的值,根据只有符号不同的两个数互为相反数,可得与的相反数.
【解答】
解:由多项式是关于的二次三项式,得
,,
的相反数是,的相反数是.
25.
【解析】
一条直线可以把平面分成两部分,两条直线最多可以把平面分成部分,三条直线最多可以把平面分成部分,四条直线最多可以把平面分成部分,可以发现,两条直线时多了部分,三条直线比原来多了部分,四条直线时比原来多了部分,…,条时比原来多了部分.
【解答】
解:如图所示,
当时,分成部分,
当时,分成部分,
当时,分成部分,…
当时,分成部分,…
规律发现,有几条线段,则分成的部分比前一种情况多几部分,
、、之间的关系是:.
故答案为:;;.
26.
【解析】
(1)根据图中线段长度,即可表示出各部分面积,进而得出两种购买方案;
(2)利用两关系式直接得出答案;
(3)①根据贷款数以及利率即可得出张先生借款后第一个月应还款数额;
②可以得出还款数额为,进而得出即可.
【解答】
解:
,
;
当时,(元);
(元);
故当时,两种方案的金额均为元.
①(元),(元).
故张先生借款后第一个月应还元.???????????
②
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
