华东师大版七年级数学上册 第4章 图形的初步认识 单元测试题(Word版 含解析)
文档属性
| 名称 | 华东师大版七年级数学上册 第4章 图形的初步认识 单元测试题(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 123.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 23:39:54 | ||
图片预览


文档简介
第4章
图形的初步认识
单元测试题
(满分120分;时间:120分钟)
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
题号
一
二
三
总分
得分
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
1.
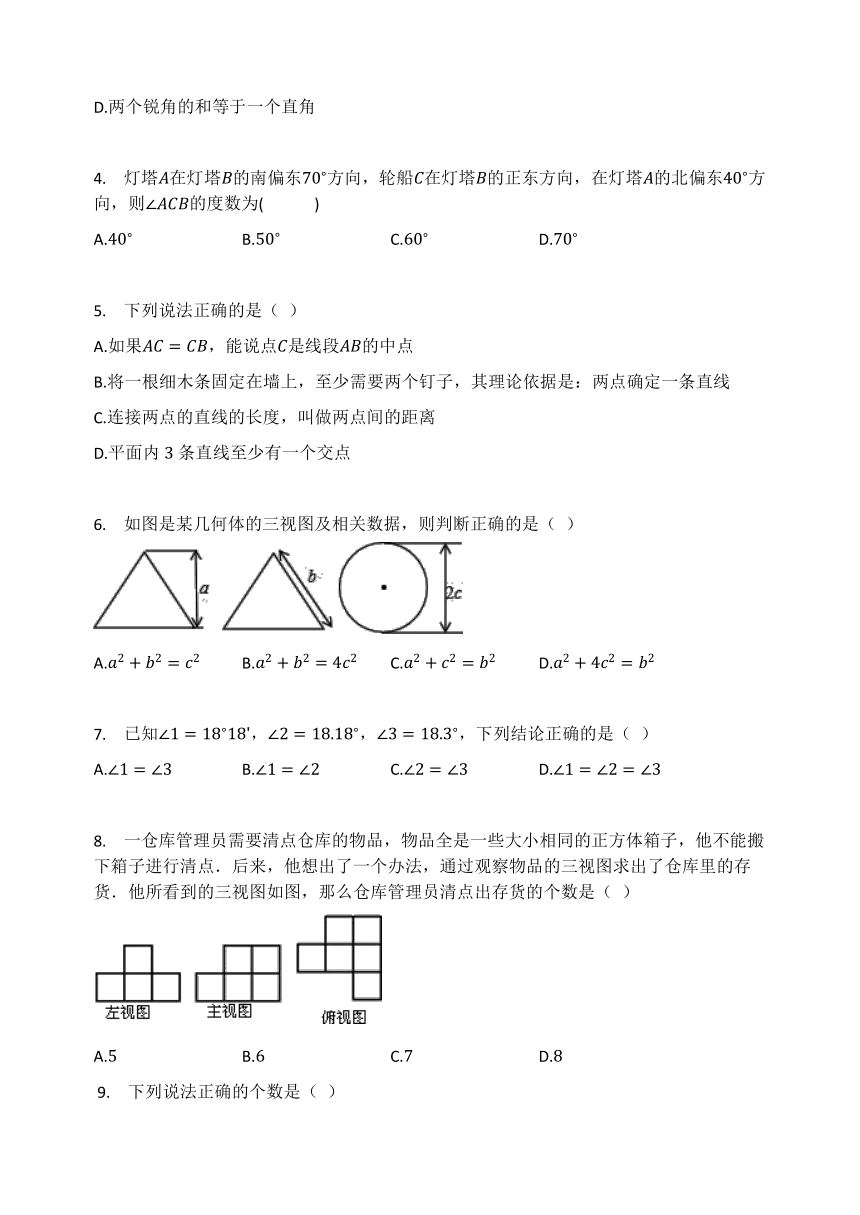
如图,在长方体中,下列关系正确的是(
)
A.棱
B.面面
C.棱面
D.面面
?
2.
如图是由个大小相同的小立方块组成的几何体,则它的俯视图是(?
?
?
?
)
A.
B.
C.
D.
?
3.
下列说法中,不正确的是(
)
A.两个直角的和等于一个平角
B.两个平角的和等于一个周角
C.点整,时针和分针组成的角的是一个平角
D.两个锐角的和等于一个直角
?
4.
灯塔在灯塔的南偏东方向,轮船在灯塔的正东方向,在灯塔的北偏东方向,则的度数为(?
?
?
?
)
A.
B.
C.
D.
?
5.
下列说法正确的是(
)
A.如果,能说点是线段的中点
B.将一根细木条固定在墙上,至少需要两个钉子,其理论依据是:两点确定一条直线
C.连接两点的直线的长度,叫做两点间的距离
D.平面内条直线至少有一个交点
?
6.
如图是某几何体的三视图及相关数据,则判断正确的是(
)
A.
B.
C.
D.
?
7.
已知,,,下列结论正确的是(
)
A.
B.
C.
D.
?
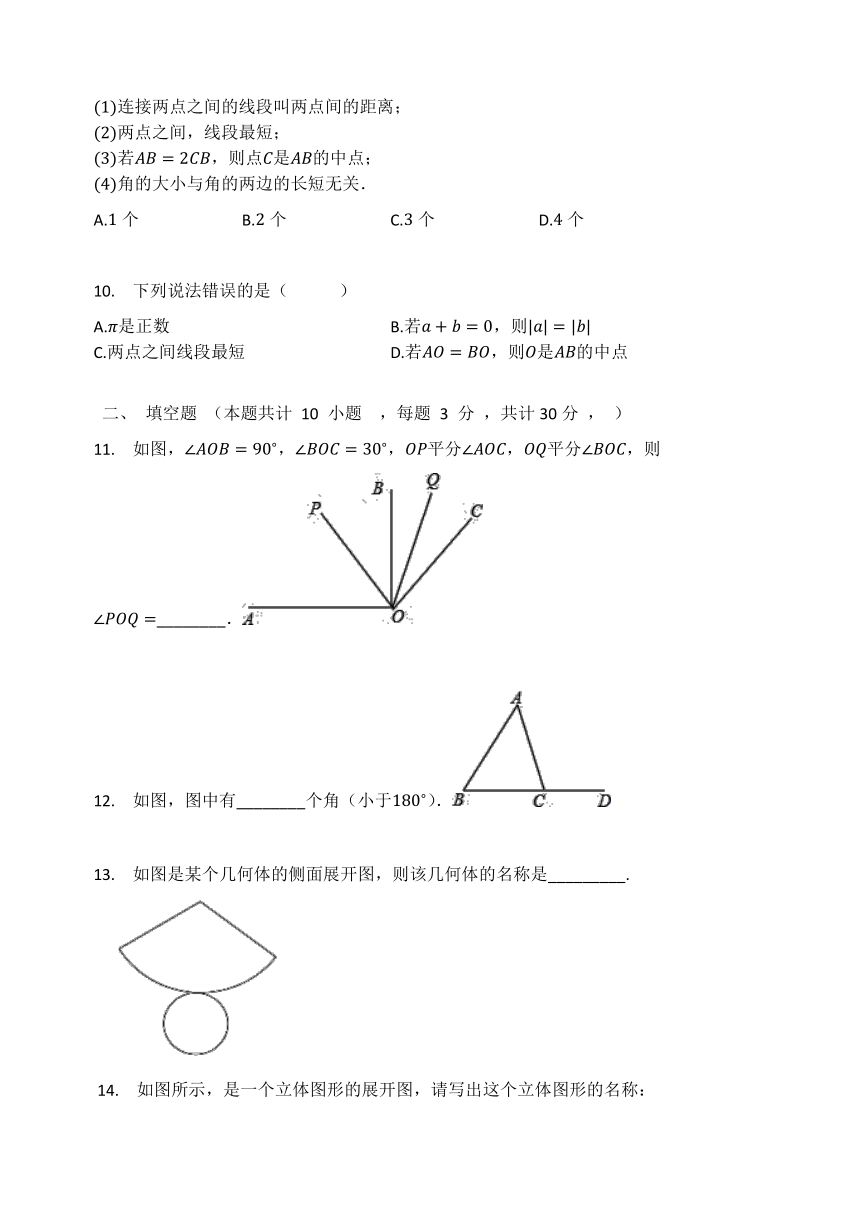
8.
一仓库管理员需要清点仓库的物品,物品全是一些大小相同的正方体箱子,他不能搬下箱子进行清点.后来,他想出了一个办法,通过观察物品的三视图求出了仓库里的存货.他所看到的三视图如图,那么仓库管理员清点出存货的个数是(
)
A.
B.
C.
D.
?9.
下列说法正确的个数是(
)
连接两点之间的线段叫两点间的距离;
两点之间,线段最短;
若,则点是的中点;
角的大小与角的两边的长短无关.
A.个
B.个
C.个
D.个
?
10.
下列说法错误的是(?
?
?
?
)
A.是正数
B.若,则
C.两点之间线段最短
D.若,则是的中点
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
如图,,,平分,平分,则________.
?
12.
如图,图中有________个角(小于).
?
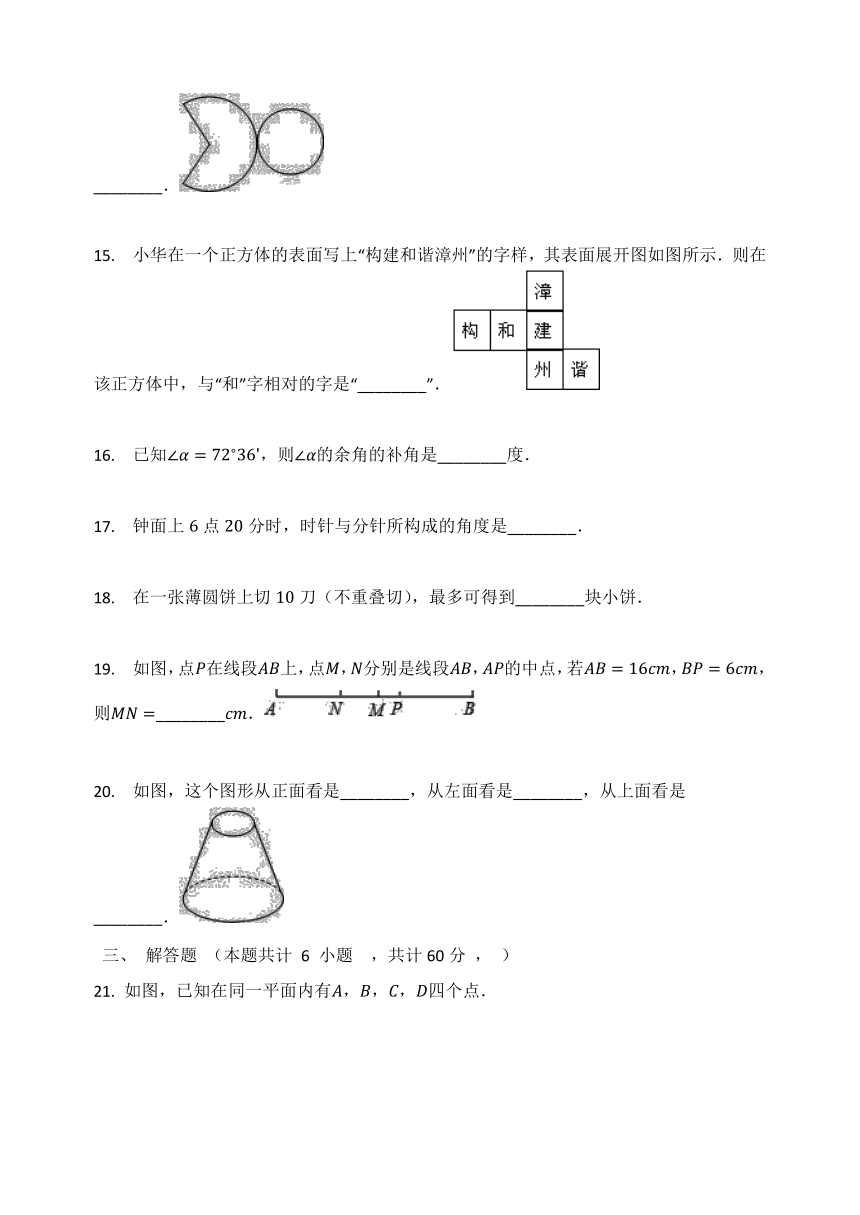
13.
如图是某个几何体的侧面展开图,则该几何体的名称是_________.
?14.
如图所示,是一个立体图形的展开图,请写出这个立体图形的名称:________.
?
15.
小华在一个正方体的表面写上“构建和谐漳州”的字样,其表面展开图如图所示.则在该正方体中,与“和”字相对的字是“________”.
?
16.
已知,则的余角的补角是________度.
?
17.
钟面上点分时,时针与分针所构成的角度是________.
?
18.
在一张薄圆饼上切刀(不重叠切),最多可得到________块小饼.
?
19.
如图,点在线段上,点,分别是线段,的中点,若,,则________.
?
20.
如图,这个图形从正面看是________,从左面看是________,从上面看是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
如图,已知在同一平面内有,,,四个点.
若点在点的北偏东方向上,则点在点的什么方向上;
在平面内找一点,使得它到四个点距离和最小,并说出你的理由.
?
22.
如图所示,把线段延长至,使,再反向延长至,=.
问:
①是的几倍?
②是的几分之几?
?
23.
一只蚂蚁从点出发,沿北偏东方向爬行厘米,碰到障碍物,又沿北偏西方向向西行厘米到.
(1)请画出蚂蚁的爬行路线;
(2)点在点的什么位置?测量出点离点有多远(精确到厘米).
?
24.
点、顺次将线段分成三部分,且,,线段的中点为,与之和为厘米.
(1)根据题意画出图形;
(2)求线段的长.
?
25.
已知线段,点为线段上的一个动点(点不与,重合),点,分别是和的中点.
若,求的长;
若点恰好是的中点,且,求的长.
?
26.
(1)如图,有一个六棱柱的房间,在房间内的一点处有一只蚂蚁,它想到房间内的另一点处去吃食物,试问它采取怎样的行走路线是最近的?(只允许走墙壁)
(2)如果是一只蜜蜂,从到怎样飞是最近的?
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【解析】
在长方体中,棱与面,面与面之间的关系有平行和垂直两种.
【解答】
解:、棱与是异面相交,故错误;
、面面,故正确;
、棱在面内,故错误;
、面面,故错误.
故选.
2.
【解析】
根据俯视图是从上面看到的图形解答即可.
【解答】
解:根据题意得到几何体的俯视图为
?
故选.
3.
【解析】
根据直角和平角的定义对进行判断;根据平角和周角的定义对进行判断;根据钟面角对进行判断;根据度与度的和不为直角可对进行判断.
【解答】
解:、两个直角的和等于一个平角,所以选项的说法正确;
、两个平角的和等于一个周角,所以选项的说法正确;
、点整,时针指向,分针指向,它们组成的角的是一个平角,所以选项的说法正确;
、两个锐角的和可能为锐角、也可能为直角,也可能为钝角,所以选项的说法错误.
故选.
4.
【解析】
此题暂无解析
【解答】
解:由题意画出示意图如图:
易知为直角三角形,,
∴
.
故选
5.
【解析】
根据两点间的距离、两点确定一条直线及线段的中点等知识,对每个选项注意判断得出正确选项.
【解答】
解:、如果,若、、在同一条直线上,则能说点是线段的中点,否则不能说是的中点,所以本选项错误;
、直线的性质为两点确定一条直线,将一根木条固定在墙上,至少需要两个钉子符合直线的性质,故本选项正确;
、连接两点的线段的长度,叫做两点间的距离,故本选项错误;
、若平面内条直线两两平行,则无交点,所以平面内条直线至少有一个交点错误;
故选:.
6.
【解析】
首先根据该几何体的三视图判断该几何体为圆锥,然后根据三视图的相关数据得到圆锥的底面上的高、母线长及底面半径,然后可以得到三者之间的关系.
【解答】
解:∵
该几何体的正视图和左视图都是等腰三角形,俯视图是圆,
∴
该几何体为圆锥,
∴
圆锥的底面半径为,高为,母线长为,
∵
圆锥的底面半径、母线及圆锥的高构成直角三角形,
∴
.
故选.
7.
【解析】
根据小单位化大单位除以进率,可化成相同单位的角,根据有理数的大小比较,可得答案.
【解答】
解:,
故选:.
8.
【解析】
主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】
解:综合主视图,俯视图,左视图底层有个正方体,第二层有个正方体,所以仓库里的正方体箱子的个数是.
故选.
9.
【解析】
根据两点之间的距离的定义,线段的中点的定义以及角的定义即可作出判断.
【解答】
解:连接两点之间的线段的长度叫两点间的距离,则命题错误;
两点之间,线段最短,正确;
当在线段上,且时,点是的中点,当不在线段上时,则不是中点,故命题错误;
角的大小与角的两边的长短无关,正确.
故正确的有、.
故选.
10.
【解析】
本题主要考查数的分类,相反数,绝对值,点、线段的概念.
【解答】
解:∵
是正数,
∴
正确;
∵
,
∴
,
∴
,
∴
正确;
∵
两点之间线段最短,
∴
正确;
∵
,三点不一定共线,
∴
不一定是的中点.
∴
错误.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【解析】
先求出,再由平分,平分,求出,,即可求出.
【解答】
解:∵
,,
∴
,
∵
平分,平分,
∴
,,
∴
;
故答案为:.
12.
【解析】
根据图形和角的概念即可判断.
【解答】
解:小于的角为锐角.
由图可得:
锐角有,,,共个.
故答案为:.
13.
【解析】
由圆锥的展开图特点断得出即可.
【解答】
解:因为圆锥的展开图为一个扇形和一个圆形,故这个几何体是圆锥.
故答案为:圆锥.
14.
【解析】
由平面图形的折叠及圆锥的展开图特点作答.
【解答】
解:因为圆锥的展开图为一个扇形和一个圆形,故这个立体图形是圆锥.
故填:圆锥.
15.
【解析】
利用正方体及其表面展开图的特点解题.
【解答】
解:这是一个正方体的平面展开图,共有六个面,
其中面“漳”与面“州”相对,
面“构”与面“建”相对,
面“和”与面“谐”相对.
故应填:谐.
16.
【解析】
根据余角和补角的定义进行求解即可.
【解答】
解:由题意,得:.
故的余角的补角是.
17.
【解析】
根据时针与分针相距的份数乘以每份的度数,可得答案.
【解答】
解:点分时,时针与分针相距,
点分时,时针与分针所构成的角度是.
故答案为:.
18.
【解析】
列举一些情况后,总结规律,根据规律求解.
【解答】
解:不切时有块,
切一刀时,有块,
切二刀时,有块,
切三刀时有块,
…
切刀时,有块,
当,块数块,
故应填.
19.
【解析】
根据线段中点求出,求出,根据线段中点求出,代入求出即可.
【解答】
解:∵
为的中点,,
∴
,
∵
,,
∴
,
∵
为的中点,
∴
,
∴
,
故答案为:.
20.
【解析】
图形为一个圆台,根据三视图的概念作答.
【解答】
解:该图形从正面看是?梯形,从左面看是梯形,从上面看是同心圆环.
故答案为:梯形,梯形,同心圆环.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【解析】
根据方向角的概念,结合题意可得点在点南偏西方向上;
如图,连接,交于点,则点即为所求,因为两点之间线段最短.
【解答】
解:如图,根据题意可得:
,
所以点在点南偏西方向上;
如图,连接,交于点,则点即为所求,
根据两点之间线段最短可得:
22.
【解析】
①先得到=,然后把,=代入整理即可;
②由得到,再根据==得到.
【解答】
①=,
∵
,=,
∴
=,
即是的倍;
②==,
∵
,即,
∴
=,
即是的七分之四.
23.
【解析】
根据方位角的概念,画图正确表示出方位角,即可求解.
【解答】
解:(1)如图所示
(2)在的正北方向,离点厘米.
24.
【解析】
(1)根据、,、、之间的比例关系画出线段即可;
(2)设线段厘米,则厘米,厘米,再由点是线段的中点即可求出的长,根据与之和为厘米即可求出的值,进而可求出的长.
【解答】
解:(1)
(2)设线段厘米,则厘米,厘米.
∵
点是线段的中点,
∴
,
∴
,,
∴
,
解得.
所以(厘米).
25.
【解析】
(1)根据中点定义,,即可求出的长;
(2)根据是的中点,即可知,易求的长;
【解答】
解:,分别是和的中点,
.
,
.
点是中点,
.
又,分别是和的中点,
,
,
故的长为.
26.
【解析】
(1)把侧展开,使点和点在同一平面,然后根据两点之间线段最短求解;
(2)如果是一只蜜蜂,则可根据两点之间线段最短直接求解.
【解答】
解:(1)把六棱柱的侧面展开,使点和点所在的侧面与正面在同一个平面,
然后连结,则线段为蚂蚁行走路线,如图;
(2)如果是一只蜜蜂,在六棱柱中
图形的初步认识
单元测试题
(满分120分;时间:120分钟)
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
题号
一
二
三
总分
得分
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
1.
如图,在长方体中,下列关系正确的是(
)
A.棱
B.面面
C.棱面
D.面面
?
2.
如图是由个大小相同的小立方块组成的几何体,则它的俯视图是(?
?
?
?
)
A.
B.
C.
D.
?
3.
下列说法中,不正确的是(
)
A.两个直角的和等于一个平角
B.两个平角的和等于一个周角
C.点整,时针和分针组成的角的是一个平角
D.两个锐角的和等于一个直角
?
4.
灯塔在灯塔的南偏东方向,轮船在灯塔的正东方向,在灯塔的北偏东方向,则的度数为(?
?
?
?
)
A.
B.
C.
D.
?
5.
下列说法正确的是(
)
A.如果,能说点是线段的中点
B.将一根细木条固定在墙上,至少需要两个钉子,其理论依据是:两点确定一条直线
C.连接两点的直线的长度,叫做两点间的距离
D.平面内条直线至少有一个交点
?
6.
如图是某几何体的三视图及相关数据,则判断正确的是(
)
A.
B.
C.
D.
?
7.
已知,,,下列结论正确的是(
)
A.
B.
C.
D.
?
8.
一仓库管理员需要清点仓库的物品,物品全是一些大小相同的正方体箱子,他不能搬下箱子进行清点.后来,他想出了一个办法,通过观察物品的三视图求出了仓库里的存货.他所看到的三视图如图,那么仓库管理员清点出存货的个数是(
)
A.
B.
C.
D.
?9.
下列说法正确的个数是(
)
连接两点之间的线段叫两点间的距离;
两点之间,线段最短;
若,则点是的中点;
角的大小与角的两边的长短无关.
A.个
B.个
C.个
D.个
?
10.
下列说法错误的是(?
?
?
?
)
A.是正数
B.若,则
C.两点之间线段最短
D.若,则是的中点
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
如图,,,平分,平分,则________.
?
12.
如图,图中有________个角(小于).
?
13.
如图是某个几何体的侧面展开图,则该几何体的名称是_________.
?14.
如图所示,是一个立体图形的展开图,请写出这个立体图形的名称:________.
?
15.
小华在一个正方体的表面写上“构建和谐漳州”的字样,其表面展开图如图所示.则在该正方体中,与“和”字相对的字是“________”.
?
16.
已知,则的余角的补角是________度.
?
17.
钟面上点分时,时针与分针所构成的角度是________.
?
18.
在一张薄圆饼上切刀(不重叠切),最多可得到________块小饼.
?
19.
如图,点在线段上,点,分别是线段,的中点,若,,则________.
?
20.
如图,这个图形从正面看是________,从左面看是________,从上面看是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
如图,已知在同一平面内有,,,四个点.
若点在点的北偏东方向上,则点在点的什么方向上;
在平面内找一点,使得它到四个点距离和最小,并说出你的理由.
?
22.
如图所示,把线段延长至,使,再反向延长至,=.
问:
①是的几倍?
②是的几分之几?
?
23.
一只蚂蚁从点出发,沿北偏东方向爬行厘米,碰到障碍物,又沿北偏西方向向西行厘米到.
(1)请画出蚂蚁的爬行路线;
(2)点在点的什么位置?测量出点离点有多远(精确到厘米).
?
24.
点、顺次将线段分成三部分,且,,线段的中点为,与之和为厘米.
(1)根据题意画出图形;
(2)求线段的长.
?
25.
已知线段,点为线段上的一个动点(点不与,重合),点,分别是和的中点.
若,求的长;
若点恰好是的中点,且,求的长.
?
26.
(1)如图,有一个六棱柱的房间,在房间内的一点处有一只蚂蚁,它想到房间内的另一点处去吃食物,试问它采取怎样的行走路线是最近的?(只允许走墙壁)
(2)如果是一只蜜蜂,从到怎样飞是最近的?
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【解析】
在长方体中,棱与面,面与面之间的关系有平行和垂直两种.
【解答】
解:、棱与是异面相交,故错误;
、面面,故正确;
、棱在面内,故错误;
、面面,故错误.
故选.
2.
【解析】
根据俯视图是从上面看到的图形解答即可.
【解答】
解:根据题意得到几何体的俯视图为
?
故选.
3.
【解析】
根据直角和平角的定义对进行判断;根据平角和周角的定义对进行判断;根据钟面角对进行判断;根据度与度的和不为直角可对进行判断.
【解答】
解:、两个直角的和等于一个平角,所以选项的说法正确;
、两个平角的和等于一个周角,所以选项的说法正确;
、点整,时针指向,分针指向,它们组成的角的是一个平角,所以选项的说法正确;
、两个锐角的和可能为锐角、也可能为直角,也可能为钝角,所以选项的说法错误.
故选.
4.
【解析】
此题暂无解析
【解答】
解:由题意画出示意图如图:
易知为直角三角形,,
∴
.
故选
5.
【解析】
根据两点间的距离、两点确定一条直线及线段的中点等知识,对每个选项注意判断得出正确选项.
【解答】
解:、如果,若、、在同一条直线上,则能说点是线段的中点,否则不能说是的中点,所以本选项错误;
、直线的性质为两点确定一条直线,将一根木条固定在墙上,至少需要两个钉子符合直线的性质,故本选项正确;
、连接两点的线段的长度,叫做两点间的距离,故本选项错误;
、若平面内条直线两两平行,则无交点,所以平面内条直线至少有一个交点错误;
故选:.
6.
【解析】
首先根据该几何体的三视图判断该几何体为圆锥,然后根据三视图的相关数据得到圆锥的底面上的高、母线长及底面半径,然后可以得到三者之间的关系.
【解答】
解:∵
该几何体的正视图和左视图都是等腰三角形,俯视图是圆,
∴
该几何体为圆锥,
∴
圆锥的底面半径为,高为,母线长为,
∵
圆锥的底面半径、母线及圆锥的高构成直角三角形,
∴
.
故选.
7.
【解析】
根据小单位化大单位除以进率,可化成相同单位的角,根据有理数的大小比较,可得答案.
【解答】
解:,
故选:.
8.
【解析】
主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】
解:综合主视图,俯视图,左视图底层有个正方体,第二层有个正方体,所以仓库里的正方体箱子的个数是.
故选.
9.
【解析】
根据两点之间的距离的定义,线段的中点的定义以及角的定义即可作出判断.
【解答】
解:连接两点之间的线段的长度叫两点间的距离,则命题错误;
两点之间,线段最短,正确;
当在线段上,且时,点是的中点,当不在线段上时,则不是中点,故命题错误;
角的大小与角的两边的长短无关,正确.
故正确的有、.
故选.
10.
【解析】
本题主要考查数的分类,相反数,绝对值,点、线段的概念.
【解答】
解:∵
是正数,
∴
正确;
∵
,
∴
,
∴
,
∴
正确;
∵
两点之间线段最短,
∴
正确;
∵
,三点不一定共线,
∴
不一定是的中点.
∴
错误.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【解析】
先求出,再由平分,平分,求出,,即可求出.
【解答】
解:∵
,,
∴
,
∵
平分,平分,
∴
,,
∴
;
故答案为:.
12.
【解析】
根据图形和角的概念即可判断.
【解答】
解:小于的角为锐角.
由图可得:
锐角有,,,共个.
故答案为:.
13.
【解析】
由圆锥的展开图特点断得出即可.
【解答】
解:因为圆锥的展开图为一个扇形和一个圆形,故这个几何体是圆锥.
故答案为:圆锥.
14.
【解析】
由平面图形的折叠及圆锥的展开图特点作答.
【解答】
解:因为圆锥的展开图为一个扇形和一个圆形,故这个立体图形是圆锥.
故填:圆锥.
15.
【解析】
利用正方体及其表面展开图的特点解题.
【解答】
解:这是一个正方体的平面展开图,共有六个面,
其中面“漳”与面“州”相对,
面“构”与面“建”相对,
面“和”与面“谐”相对.
故应填:谐.
16.
【解析】
根据余角和补角的定义进行求解即可.
【解答】
解:由题意,得:.
故的余角的补角是.
17.
【解析】
根据时针与分针相距的份数乘以每份的度数,可得答案.
【解答】
解:点分时,时针与分针相距,
点分时,时针与分针所构成的角度是.
故答案为:.
18.
【解析】
列举一些情况后,总结规律,根据规律求解.
【解答】
解:不切时有块,
切一刀时,有块,
切二刀时,有块,
切三刀时有块,
…
切刀时,有块,
当,块数块,
故应填.
19.
【解析】
根据线段中点求出,求出,根据线段中点求出,代入求出即可.
【解答】
解:∵
为的中点,,
∴
,
∵
,,
∴
,
∵
为的中点,
∴
,
∴
,
故答案为:.
20.
【解析】
图形为一个圆台,根据三视图的概念作答.
【解答】
解:该图形从正面看是?梯形,从左面看是梯形,从上面看是同心圆环.
故答案为:梯形,梯形,同心圆环.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【解析】
根据方向角的概念,结合题意可得点在点南偏西方向上;
如图,连接,交于点,则点即为所求,因为两点之间线段最短.
【解答】
解:如图,根据题意可得:
,
所以点在点南偏西方向上;
如图,连接,交于点,则点即为所求,
根据两点之间线段最短可得:
22.
【解析】
①先得到=,然后把,=代入整理即可;
②由得到,再根据==得到.
【解答】
①=,
∵
,=,
∴
=,
即是的倍;
②==,
∵
,即,
∴
=,
即是的七分之四.
23.
【解析】
根据方位角的概念,画图正确表示出方位角,即可求解.
【解答】
解:(1)如图所示
(2)在的正北方向,离点厘米.
24.
【解析】
(1)根据、,、、之间的比例关系画出线段即可;
(2)设线段厘米,则厘米,厘米,再由点是线段的中点即可求出的长,根据与之和为厘米即可求出的值,进而可求出的长.
【解答】
解:(1)
(2)设线段厘米,则厘米,厘米.
∵
点是线段的中点,
∴
,
∴
,,
∴
,
解得.
所以(厘米).
25.
【解析】
(1)根据中点定义,,即可求出的长;
(2)根据是的中点,即可知,易求的长;
【解答】
解:,分别是和的中点,
.
,
.
点是中点,
.
又,分别是和的中点,
,
,
故的长为.
26.
【解析】
(1)把侧展开,使点和点在同一平面,然后根据两点之间线段最短求解;
(2)如果是一只蜜蜂,则可根据两点之间线段最短直接求解.
【解答】
解:(1)把六棱柱的侧面展开,使点和点所在的侧面与正面在同一个平面,
然后连结,则线段为蚂蚁行走路线,如图;
(2)如果是一只蜜蜂,在六棱柱中
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
