人教版八年级数学上册 14.1.1同底数幂的乘法 课件(18张)
文档属性
| 名称 | 人教版八年级数学上册 14.1.1同底数幂的乘法 课件(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 280.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 08:39:48 | ||
图片预览





文档简介
(共18张PPT)
14.1.1同底数幂的乘法
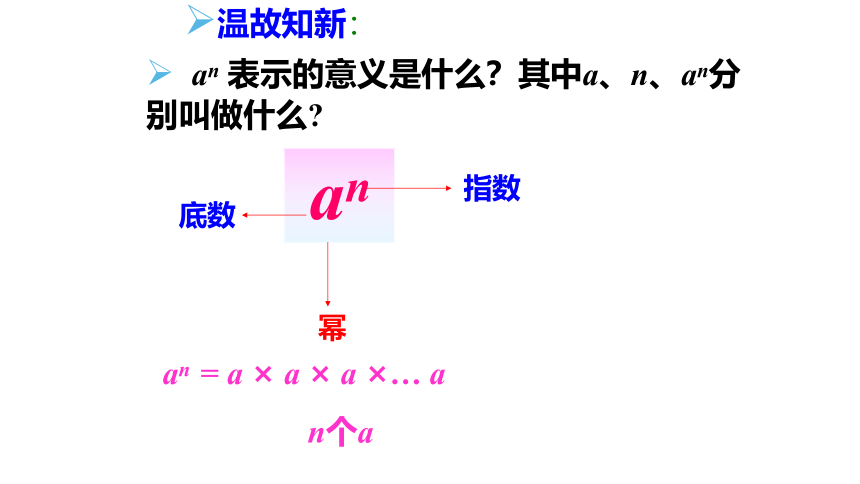
an
表示的意义是什么?其中a、n、an分
别叫做什么?
an
底数
幂
指数
温故知新:
an
=
a
×
a
×
a
×…
a
n个a
25表示什么?
10×10×10×10×10
可以写成什么形式?
温故知新:
25
=
.
?
2×2×2×2×2
105
10×10×10×10×10
=
.
(乘方的意义)
(乘方的意义)
一、新知学习
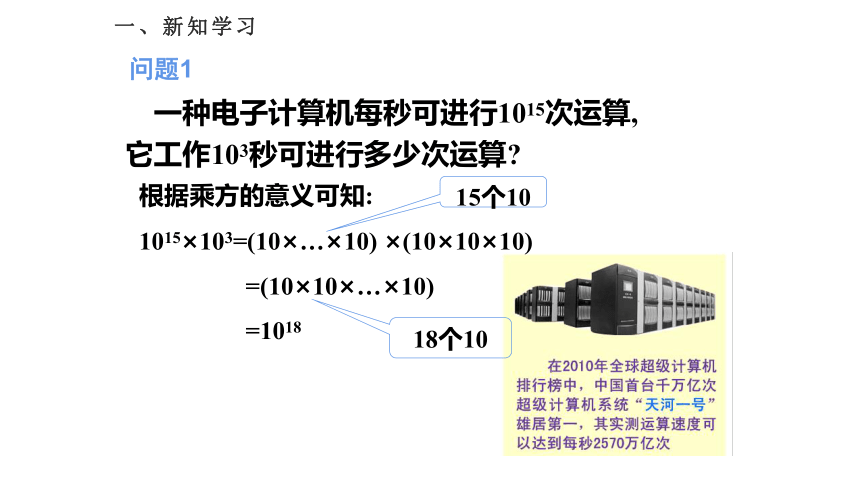
一种电子计算机每秒可进行1015次运算,它工作103秒可进行多少次运算?
根据乘方的意义可知:
1015×103=(10×…×10)
×(10×10×10)
=(10×10×…×10)
=1018
15个10
18个10
问题1
(1)25×22=2
(
)
根据乘方的意义填空,观察计算结果,你能发现什么规律?
探究
=(2×2×2×2×2)
×(2×2)
=2×2×2×2×2×
2×2
=27
(2)a3·a2=a(
)
=(a﹒a﹒a)
(a﹒a)
=a﹒a﹒a﹒a﹒a
=a5
7
5
一、新知学习
探究在线:
请同学们观察下面各题左右两边,底数、指数有什么关系?
103
×102
=
10(
)
23
×22
=
2(
)
a3×
a2
=
a(
)
5
5
5
猜想:
am
·
an=
?
(当m、n都是正整数)
.
猜想:
am
·
an=
(当m、n都是正整数)
真不错,你的猜想是正确的!
m个a
n个a
=
aa…a
(m+n)个a
即
am
·
an
=
am+n
(当m、n都是正整数)
(aa…a)
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
=am+n
am
·
an
=
即
(乘方的意义)
(乘法结合律)
(乘方的意义)
am
·
an
=
am+n
(当m、n都是正整数)
同底数幂相乘,
想一想:
当三个或三个以上同底数幂相乘时,是否也
?
具有这一性质呢?
怎样用公式表示?
底数 ,指数 。
不变
相加
同底数幂的乘法性质:
如
am·an·ap
=
am+n+p
(m、n、p都是正整数)
夯实新知:
判断下列计算是否正确,并说明理由
?
?
?
?
?
√
×
×
×
×
例1
计算:
(1)
x2·x5;
(2)
a·a6;
(3)
2×24×23;
(4)
xm·x3m+1.
解:
(1)x2·x5
=x2+5
=x
7.
(4)
xm·x3m+1=xm+3m+1
=
x
4m+1.
(3)2×24×23=21+4+3=28.
(2)
a·a6
=a1+6
=a7.
二、新知运用
解:(1)
(a-b)3
·
(a-b)4
=
(a-b)3+4
=(a-b)7;
(2)(m+n)3
·(m+n)5
·(m+n)7
=(m+n)3+5+7=(m+n)15;
例2
计算:
(1)(a-b)3
·
(a-b)4
;
(2)(m+n)3
·(m+n)5
·(m+n)7
;
(3)(x-y)2·(y-x)5.
(3)(x-y)2·(y-x)5=(y-x)2(y-x)5
=(y-x)2+5=(y-x)7.
方法总结:公式am
·
an
=
am+n中的底数a不仅可以代表数、单项式,还可以代表多项式等其他代数式.当底数互为相反数的幂相乘时,先把底数统一,再进行计算.
n为偶数
n为奇数
1.计算:
(1)107
×104
;
(2)x2
·
x5
.
解:(1)107
×104
=107
+
4=
1011
(2)x2
·
x5
=
x2
+
5
=
x7
2.计算:
(1)23×24×25
(2)y
·
y2
·
y3
解:(1)23×24×25=23+4+5=212
(2)y
·
y2
·
y3
=
y1+2+3=y6
am
·
an
=
am+n
(当m、n都是正整数)
am·an·ap
=
am+n+p
(m、n、p都是正整数)
想一想:am+n可以写成哪两个因式的积?
同底数幂乘法法则的逆用
am+n
=
am
·
an
填一填:若xm
=3
,xn
=2,那么,
(1)xm+n
=
×
=
×
=
;
(2)x2m
=
×
=
×
=
;
(3)x2m+n
=
×
=
×
=
.
xm
xn
6
3
2
xm
xm
3
3
9
x2m
xn
9
2
18
例3
(1)若xa=3,xb=4,xc=5,求2xa+b+c的值.
(2)已知23x+2=32,求x的值;
(2)
∵
23x+2=32=25,
∴3x+2=5,
∴x=1.
解:(1)
2xa+b+c=2xa·xb·xc=120.
方法总结:(1)关键是逆用同底数幂的乘法公式,将所求代数式转化为几个已知因式的乘积的形式,然后再求值.
(2)关键是将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
填空:(1)
的结果是______.
(2)
(
)
=
xm
·(
)=x3m
_________.
(3)已知
,且
求
的值。
当堂检测:
9
4、已知2x+2=20,求2x的值。
5、已知am=4,an=16,
则am+n=____
6、若x5=32,x3=8,则x8=____
14.1.1同底数幂的乘法
an
表示的意义是什么?其中a、n、an分
别叫做什么?
an
底数
幂
指数
温故知新:
an
=
a
×
a
×
a
×…
a
n个a
25表示什么?
10×10×10×10×10
可以写成什么形式?
温故知新:
25
=
.
?
2×2×2×2×2
105
10×10×10×10×10
=
.
(乘方的意义)
(乘方的意义)
一、新知学习
一种电子计算机每秒可进行1015次运算,它工作103秒可进行多少次运算?
根据乘方的意义可知:
1015×103=(10×…×10)
×(10×10×10)
=(10×10×…×10)
=1018
15个10
18个10
问题1
(1)25×22=2
(
)
根据乘方的意义填空,观察计算结果,你能发现什么规律?
探究
=(2×2×2×2×2)
×(2×2)
=2×2×2×2×2×
2×2
=27
(2)a3·a2=a(
)
=(a﹒a﹒a)
(a﹒a)
=a﹒a﹒a﹒a﹒a
=a5
7
5
一、新知学习
探究在线:
请同学们观察下面各题左右两边,底数、指数有什么关系?
103
×102
=
10(
)
23
×22
=
2(
)
a3×
a2
=
a(
)
5
5
5
猜想:
am
·
an=
?
(当m、n都是正整数)
.
猜想:
am
·
an=
(当m、n都是正整数)
真不错,你的猜想是正确的!
m个a
n个a
=
aa…a
(m+n)个a
即
am
·
an
=
am+n
(当m、n都是正整数)
(aa…a)
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
=am+n
am
·
an
=
即
(乘方的意义)
(乘法结合律)
(乘方的意义)
am
·
an
=
am+n
(当m、n都是正整数)
同底数幂相乘,
想一想:
当三个或三个以上同底数幂相乘时,是否也
?
具有这一性质呢?
怎样用公式表示?
底数 ,指数 。
不变
相加
同底数幂的乘法性质:
如
am·an·ap
=
am+n+p
(m、n、p都是正整数)
夯实新知:
判断下列计算是否正确,并说明理由
?
?
?
?
?
√
×
×
×
×
例1
计算:
(1)
x2·x5;
(2)
a·a6;
(3)
2×24×23;
(4)
xm·x3m+1.
解:
(1)x2·x5
=x2+5
=x
7.
(4)
xm·x3m+1=xm+3m+1
=
x
4m+1.
(3)2×24×23=21+4+3=28.
(2)
a·a6
=a1+6
=a7.
二、新知运用
解:(1)
(a-b)3
·
(a-b)4
=
(a-b)3+4
=(a-b)7;
(2)(m+n)3
·(m+n)5
·(m+n)7
=(m+n)3+5+7=(m+n)15;
例2
计算:
(1)(a-b)3
·
(a-b)4
;
(2)(m+n)3
·(m+n)5
·(m+n)7
;
(3)(x-y)2·(y-x)5.
(3)(x-y)2·(y-x)5=(y-x)2(y-x)5
=(y-x)2+5=(y-x)7.
方法总结:公式am
·
an
=
am+n中的底数a不仅可以代表数、单项式,还可以代表多项式等其他代数式.当底数互为相反数的幂相乘时,先把底数统一,再进行计算.
n为偶数
n为奇数
1.计算:
(1)107
×104
;
(2)x2
·
x5
.
解:(1)107
×104
=107
+
4=
1011
(2)x2
·
x5
=
x2
+
5
=
x7
2.计算:
(1)23×24×25
(2)y
·
y2
·
y3
解:(1)23×24×25=23+4+5=212
(2)y
·
y2
·
y3
=
y1+2+3=y6
am
·
an
=
am+n
(当m、n都是正整数)
am·an·ap
=
am+n+p
(m、n、p都是正整数)
想一想:am+n可以写成哪两个因式的积?
同底数幂乘法法则的逆用
am+n
=
am
·
an
填一填:若xm
=3
,xn
=2,那么,
(1)xm+n
=
×
=
×
=
;
(2)x2m
=
×
=
×
=
;
(3)x2m+n
=
×
=
×
=
.
xm
xn
6
3
2
xm
xm
3
3
9
x2m
xn
9
2
18
例3
(1)若xa=3,xb=4,xc=5,求2xa+b+c的值.
(2)已知23x+2=32,求x的值;
(2)
∵
23x+2=32=25,
∴3x+2=5,
∴x=1.
解:(1)
2xa+b+c=2xa·xb·xc=120.
方法总结:(1)关键是逆用同底数幂的乘法公式,将所求代数式转化为几个已知因式的乘积的形式,然后再求值.
(2)关键是将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
填空:(1)
的结果是______.
(2)
(
)
=
xm
·(
)=x3m
_________.
(3)已知
,且
求
的值。
当堂检测:
9
4、已知2x+2=20,求2x的值。
5、已知am=4,an=16,
则am+n=____
6、若x5=32,x3=8,则x8=____
