数学:1.3.1《单调性与最大(小)值》课件(新人教A版必修1)
文档属性
| 名称 | 数学:1.3.1《单调性与最大(小)值》课件(新人教A版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 233.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-17 00:00:00 | ||
图片预览




文档简介
(共35张PPT)
学校准备建造一个长方形的花坛,面积设计为16平方米。
由于周围环境的限制,其中一边的长度既不能超过10米,又不能少于2米。求花坛长与宽两边之和的最小值和最大值。
16平方米
设长方形受限制一边长为 x 米,
归结为数学问题:
x
16平方米
利用不等式可求最小值;
如何求最大值?
研究y随x的变化而变化的规律
1.3.1 单调性与最大(小)值
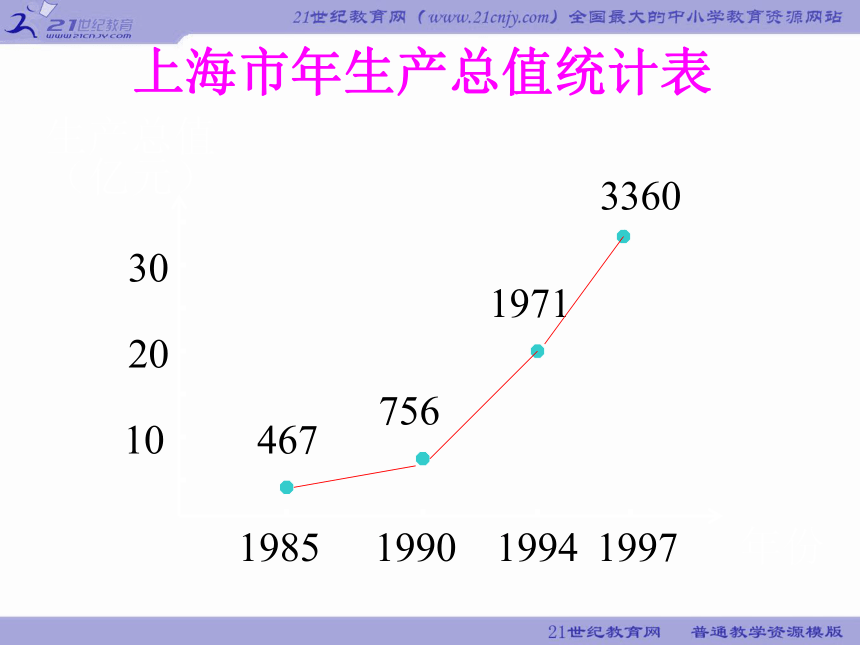
上海市年生产总值统计表
年份
生产总值
(亿元)
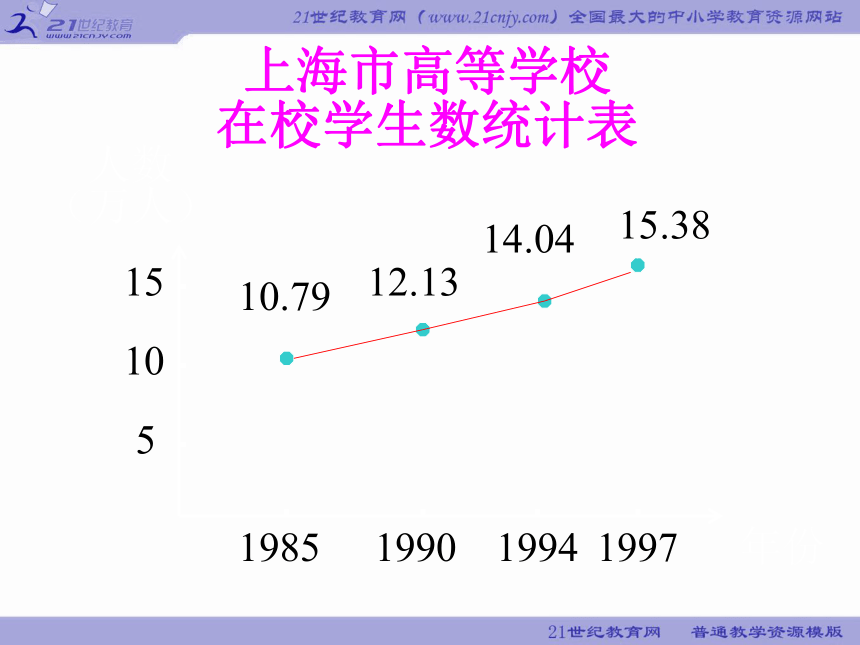
上海市高等学校
在校学生数统计表
年份
人数
(万人)
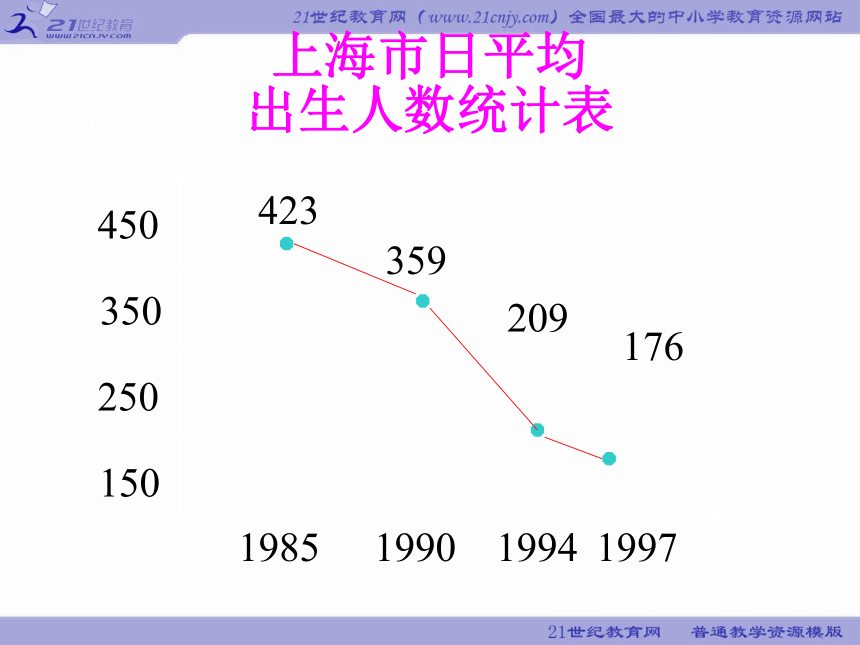
上海市日平均
出生人数统计表
年份
人数(人)
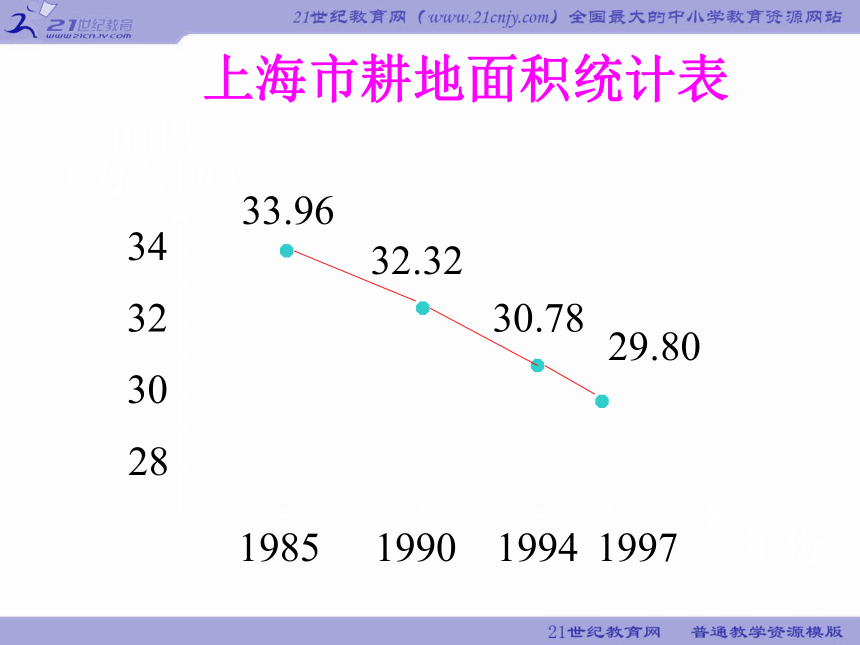
上海市耕地面积统计表
年份
面积
(万公顷)
O
x
y
oO
x
y
O
x
y
2
1
y
O
x
y
x
o
o
o
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
函数f (x)在给定区间上为增函数。
O
x
y
如何用x与 f(x)来描述上升的图象?
如何用x与 f(x)来描述下降的图象?
函数f (x)在给定区间上为减函数。
O
x
y
单调递增区间:
单调递减区间:
x
y
2
1
o
[引例]的继续:
如何判断函数
方法一
方法二
方法三
证明
[引例]的继续:
如何应用函数
课堂小结:
(1)函数单调性的概念;
(2)判断函数单调区间的常用方法;
(3)解决实际问题的数学思想方法。
(2)
(3)
作业
(1)
函数单调性的概念:
1. 如果对于属于这个区间的自变量的任意
称函数 f(x)在这个区间上是增函数。
2. 如果对于属于这个区间的自变量的任意
称函数 f(x)在这个区间上是减函数。
一般地,对于给定区间上的函数f(x):
方法一:分析函数值大小的变化。
方法二:分析函数的图象。
方法三:比较大小过程中的数值分析。
判断函数单调区间的常用方法:
方法一
方法二
方法三
解决实际问题的数学思想方法:
实际问题
数学问题
实际问题的解
数学问题的解
建立数学模型
实践验证
求解
有解吗?
作业:
P43 3、4、5
同学们再见!
证明:
方法一:分析函数值大小的变化。
x
y
9
8
6
5
4
3
7
10
2
10. 8
10
8. 7
8. 2
8
8. 3
9. 3
11.6
10
单调递减区间:
单调递增区间:
猜测:
[2,4]
[4,10]
O
x
y
4
4
8
8
12
12
16
16
10
2
6
14
方法二:分析和函数的图象
猜测:
单调递减区间:
[2,4]
单调递增区间:
[4,10]
方法三:比较大小过程中的数值分析。
解:
证明:
(条件)
(论证结果)
(结论)
学校准备建造一个长方形的花坛,面积设计为16平方米。
由于周围环境的限制,其中一边的长度既不能超过10米,又不能少于2米。求花坛长与宽两边之和的最小值和最大值。
16平方米
设长方形受限制一边长为 x 米,
归结为数学问题:
x
16平方米
利用不等式可求最小值;
如何求最大值?
研究y随x的变化而变化的规律
1.3.1 单调性与最大(小)值
上海市年生产总值统计表
年份
生产总值
(亿元)
上海市高等学校
在校学生数统计表
年份
人数
(万人)
上海市日平均
出生人数统计表
年份
人数(人)
上海市耕地面积统计表
年份
面积
(万公顷)
O
x
y
oO
x
y
O
x
y
2
1
y
O
x
y
x
o
o
o
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
函数f (x)在给定区间上为增函数。
O
x
y
如何用x与 f(x)来描述上升的图象?
如何用x与 f(x)来描述下降的图象?
函数f (x)在给定区间上为减函数。
O
x
y
单调递增区间:
单调递减区间:
x
y
2
1
o
[引例]的继续:
如何判断函数
方法一
方法二
方法三
证明
[引例]的继续:
如何应用函数
课堂小结:
(1)函数单调性的概念;
(2)判断函数单调区间的常用方法;
(3)解决实际问题的数学思想方法。
(2)
(3)
作业
(1)
函数单调性的概念:
1. 如果对于属于这个区间的自变量的任意
称函数 f(x)在这个区间上是增函数。
2. 如果对于属于这个区间的自变量的任意
称函数 f(x)在这个区间上是减函数。
一般地,对于给定区间上的函数f(x):
方法一:分析函数值大小的变化。
方法二:分析函数的图象。
方法三:比较大小过程中的数值分析。
判断函数单调区间的常用方法:
方法一
方法二
方法三
解决实际问题的数学思想方法:
实际问题
数学问题
实际问题的解
数学问题的解
建立数学模型
实践验证
求解
有解吗?
作业:
P43 3、4、5
同学们再见!
证明:
方法一:分析函数值大小的变化。
x
y
9
8
6
5
4
3
7
10
2
10. 8
10
8. 7
8. 2
8
8. 3
9. 3
11.6
10
单调递减区间:
单调递增区间:
猜测:
[2,4]
[4,10]
O
x
y
4
4
8
8
12
12
16
16
10
2
6
14
方法二:分析和函数的图象
猜测:
单调递减区间:
[2,4]
单调递增区间:
[4,10]
方法三:比较大小过程中的数值分析。
解:
证明:
(条件)
(论证结果)
(结论)
