数学:1.3.1《函数单调性(1)》课件(新人教A版必修1)
文档属性
| 名称 | 数学:1.3.1《函数单调性(1)》课件(新人教A版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 164.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-17 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
1.3.1函数的单调性
一、问题提出
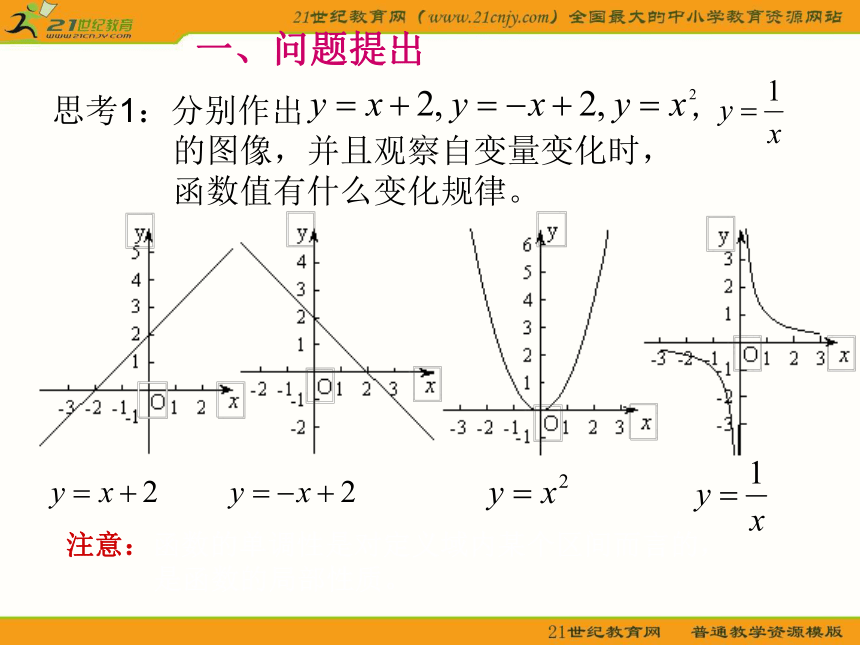
思考1:分别作出
的图像,并且观察自变量变化时,
函数值有什么变化规律。
注意:函数的单调性是对定义域内某个区间而言的,
是函数的局部性质。
思考2:能否根据自己的理解说说什么是增函数,
什么是减函数?
(1)如果函数在某个区间上随着自变量x的增大,
y也越来越大,我们就说函数在该区间上为增函数。
(2)如果函数在某个区间上随着自变量x的增大,
y越来越小,我们就说函数在该区间上为减函数。
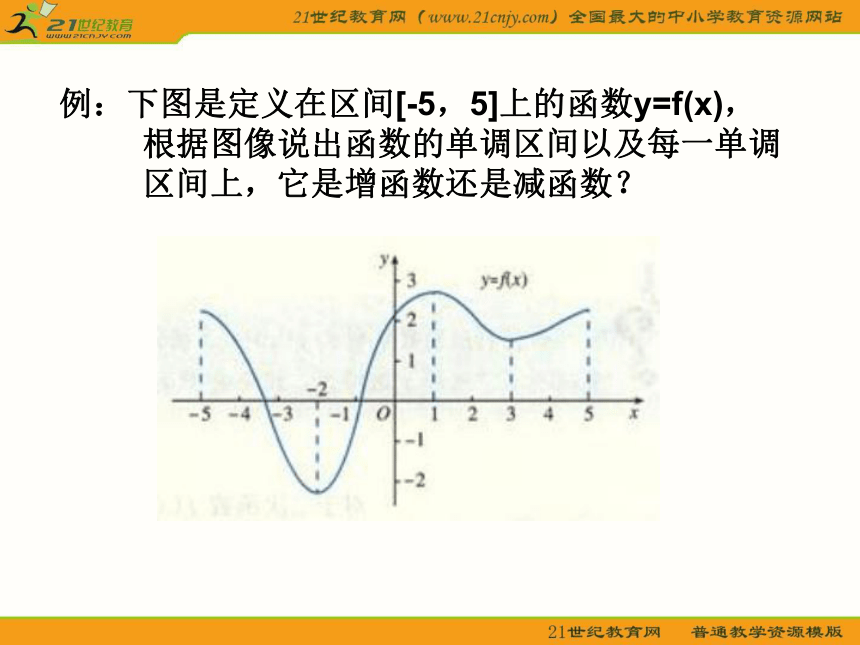
例:下图是定义在区间[-5,5]上的函数y=f(x),
根据图像说出函数的单调区间以及每一单调
区间上,它是增函数还是减函数?
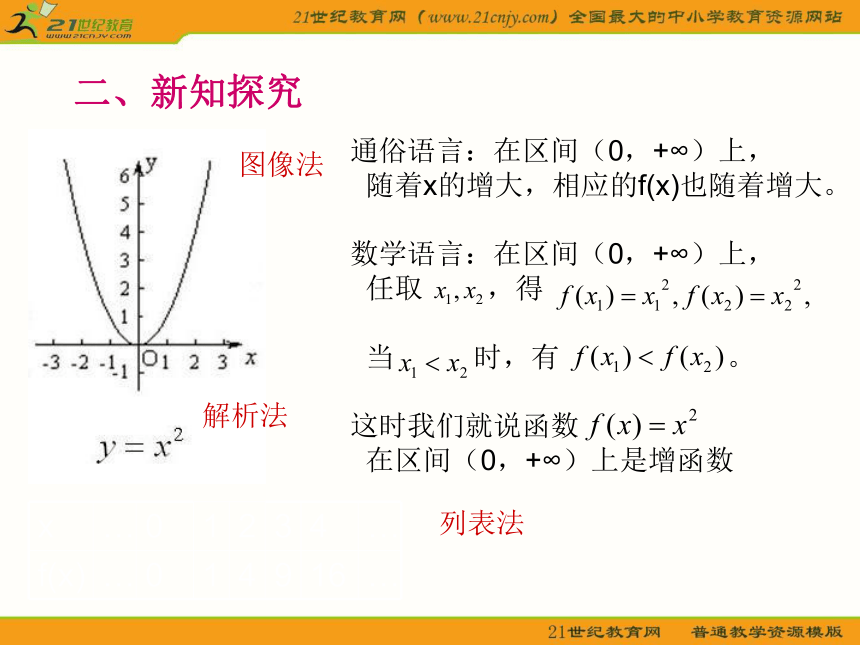
二、新知探究
解析法
图像法
通俗语言:在区间(0,+∞)上,
随着x的增大,相应的f(x)也随着增大。
数学语言:在区间(0,+∞)上,
任取 ,得
当 时,有 。
这时我们就说函数
在区间(0,+∞)上是增函数
x … 0 1 2 3 4 …
f(x) … 0 1 4 9 16 …
列表法
定义:
一般地,设函数f(x)的定义域为I,如果对于定义域I
内某个区间D上的任意两个自变量的值 ,
当 时,都有 ,那么就说f(x)在区间
D上是增函数。
一般地,设函数f(x)的定义域为I,如果对于定义域I
内某个区间D上的任意两个自变量的值 ,
当 时,都有 ,那么就说f(x)在区间
D上是减函数。
**如果函数y=f(x)在区间D上是增函数或减函数,
那么就说函数y=f(x)在这一区间具有单调性,
区间D叫做y=f(x)的单调区间。
判断题:
(1)已知f(x)=1/x ,因为f(-1)增函数。
(2)若函数f(x)满足f (2)上为增函数。
(3)若函数f(x)在区间(1,2]和(2,3)上均为增函数,
则函数f(x)在(1,3)上为增函数。
(4)因为函数f(x)=1/x在区间(-∞,0)和(0,+∞)
上都是减函数,所以f(x)=1/x在(-∞,0)∪(0,+∞)
上是减函数。
注意:
①单调性是对定义域内某个区间而言的,
离开了定义域和相应区间就谈不上单调性.
②对于某个具体函数的单调区间,
可以是整个定义域(如一次函数),可以是定义域内
某个区间(如二次函数),也可以根本不单调(如常函数).
③函数在定义域内的两个区间A,B上都是增(或减)
函数,一般不能认为函数在A∪B上是增(或减)函数.
例1:证明f(x)=-2x+1在R上是减函数。
例2:证明 在[0, +∞)上是增函数。
用定义证明函数单调性的步骤:
1.任取
2.作差
3.变形
4.定号
5.结论
三、知识迁移
例3:证明函数 在区间(- ∞, 1]
上是增函数。
例4:证明函数 在[2,6]上是减函数。
例5:证明函数 上是增函数。
例6:证明函数 在R上是增函数。
证明:任取
例7:证明函数 在其定义域内
是减函数。
例7:证明函数 在其定义域内
是减函数。
思考
(1)如果函数f(x)在区间D上是增函数,
函数g(x)在区间D上是增函数。
问:函数F(x)=f(x)+g(x)在D上是否仍为增函数?
为什么?
所以函数F(x)=f(x)+g(x)在D上是否仍为增函数
是
(2)如果函数f(x)在区间D上是减函数,
函数g(x)在区间D上是减函数。
问:函数F(x)=f(x)+g(x)在D上是否仍为减函数?
为什么?
(3)如果函数f(x)在区间D上是减函数,
函数g(x)在区间D上是增函数。
问:能否确定函数F(x)=f(x)+g(x)的单调性?
反例:f(x)=x在R上是增函数,g(x)=-x在R上是减函数
此时 F(x)= f(x)+ g(x)=x-x=0为常函数,不具有单调性
不能
是
四、小结
1.概念探究过程:从直观到抽象、从特殊到一般。
2.用定义证明函数的单调性。
3.数学思想方法和思维方法:数形结合
1.3.1函数的单调性
一、问题提出
思考1:分别作出
的图像,并且观察自变量变化时,
函数值有什么变化规律。
注意:函数的单调性是对定义域内某个区间而言的,
是函数的局部性质。
思考2:能否根据自己的理解说说什么是增函数,
什么是减函数?
(1)如果函数在某个区间上随着自变量x的增大,
y也越来越大,我们就说函数在该区间上为增函数。
(2)如果函数在某个区间上随着自变量x的增大,
y越来越小,我们就说函数在该区间上为减函数。
例:下图是定义在区间[-5,5]上的函数y=f(x),
根据图像说出函数的单调区间以及每一单调
区间上,它是增函数还是减函数?
二、新知探究
解析法
图像法
通俗语言:在区间(0,+∞)上,
随着x的增大,相应的f(x)也随着增大。
数学语言:在区间(0,+∞)上,
任取 ,得
当 时,有 。
这时我们就说函数
在区间(0,+∞)上是增函数
x … 0 1 2 3 4 …
f(x) … 0 1 4 9 16 …
列表法
定义:
一般地,设函数f(x)的定义域为I,如果对于定义域I
内某个区间D上的任意两个自变量的值 ,
当 时,都有 ,那么就说f(x)在区间
D上是增函数。
一般地,设函数f(x)的定义域为I,如果对于定义域I
内某个区间D上的任意两个自变量的值 ,
当 时,都有 ,那么就说f(x)在区间
D上是减函数。
**如果函数y=f(x)在区间D上是增函数或减函数,
那么就说函数y=f(x)在这一区间具有单调性,
区间D叫做y=f(x)的单调区间。
判断题:
(1)已知f(x)=1/x ,因为f(-1)
(2)若函数f(x)满足f (2)
(3)若函数f(x)在区间(1,2]和(2,3)上均为增函数,
则函数f(x)在(1,3)上为增函数。
(4)因为函数f(x)=1/x在区间(-∞,0)和(0,+∞)
上都是减函数,所以f(x)=1/x在(-∞,0)∪(0,+∞)
上是减函数。
注意:
①单调性是对定义域内某个区间而言的,
离开了定义域和相应区间就谈不上单调性.
②对于某个具体函数的单调区间,
可以是整个定义域(如一次函数),可以是定义域内
某个区间(如二次函数),也可以根本不单调(如常函数).
③函数在定义域内的两个区间A,B上都是增(或减)
函数,一般不能认为函数在A∪B上是增(或减)函数.
例1:证明f(x)=-2x+1在R上是减函数。
例2:证明 在[0, +∞)上是增函数。
用定义证明函数单调性的步骤:
1.任取
2.作差
3.变形
4.定号
5.结论
三、知识迁移
例3:证明函数 在区间(- ∞, 1]
上是增函数。
例4:证明函数 在[2,6]上是减函数。
例5:证明函数 上是增函数。
例6:证明函数 在R上是增函数。
证明:任取
例7:证明函数 在其定义域内
是减函数。
例7:证明函数 在其定义域内
是减函数。
思考
(1)如果函数f(x)在区间D上是增函数,
函数g(x)在区间D上是增函数。
问:函数F(x)=f(x)+g(x)在D上是否仍为增函数?
为什么?
所以函数F(x)=f(x)+g(x)在D上是否仍为增函数
是
(2)如果函数f(x)在区间D上是减函数,
函数g(x)在区间D上是减函数。
问:函数F(x)=f(x)+g(x)在D上是否仍为减函数?
为什么?
(3)如果函数f(x)在区间D上是减函数,
函数g(x)在区间D上是增函数。
问:能否确定函数F(x)=f(x)+g(x)的单调性?
反例:f(x)=x在R上是增函数,g(x)=-x在R上是减函数
此时 F(x)= f(x)+ g(x)=x-x=0为常函数,不具有单调性
不能
是
四、小结
1.概念探究过程:从直观到抽象、从特殊到一般。
2.用定义证明函数的单调性。
3.数学思想方法和思维方法:数形结合
