数学:1.3.1《函数单调性(2)》课件(新人教A版必修1)
文档属性
| 名称 | 数学:1.3.1《函数单调性(2)》课件(新人教A版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 184.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-17 00:00:00 | ||
图片预览



文档简介
(共13张PPT)
1.3.1 单调性与最大(小)值
第二课时 函数的最值
问题提出
1.确定函数的单调性有哪些手段和方法?
2.函数图象上升与下降反映了函数的单调性,
如果函数的图象存在最高点或最低点,它又
反映了函数的什么性质?
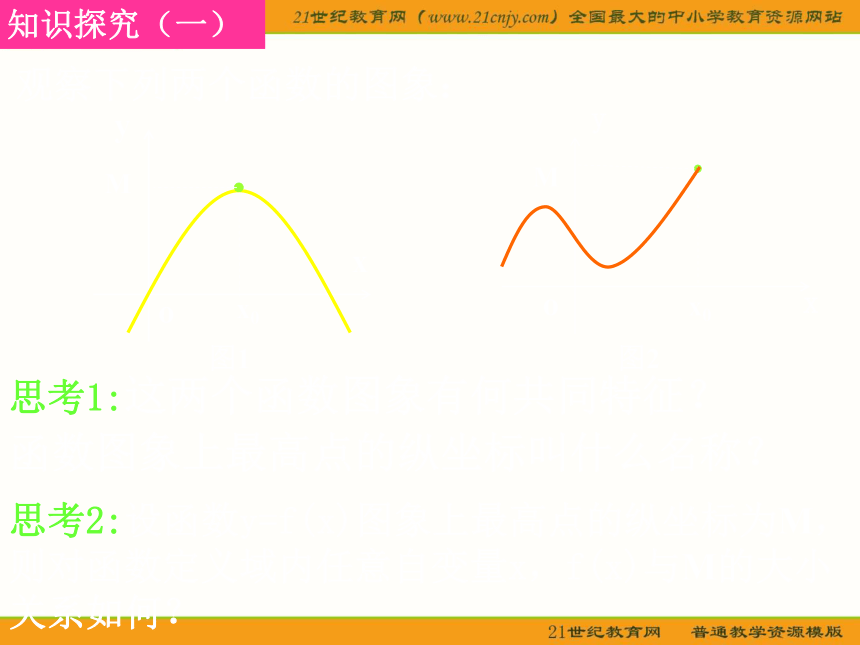
知识探究(一)
观察下列两个函数的图象:
图1
o
x0
x
M
y
思考1:这两个函数图象有何共同特征?
思考2:设函数y=f(x)图象上最高点的纵坐标为M,
则对函数定义域内任意自变量x,f(x)与M的大小
关系如何?
y
x
o
x0
图2
M
函数图象上最高点的纵坐标叫什么名称?
思考3:设函数 ,则 成立吗?
的最大值是2吗?为什么?
思考4:怎样定义函数 的最大值?用什么符号
表示?
一般地,设函数 的定义域为I,如果存在
实数M满足:
(1)对于任意的 , 都有 ;
(2)存在 ,使得 .
那么称M是函数 的最大值,记作
思考5:函数的最大值是函数值域中的一个元
素吗?如果函数 的值域是(a,b),则函
数 存在最大值吗?
思考6:函数 有最大
值吗?为什么?
图1
y
o
x0
x
m
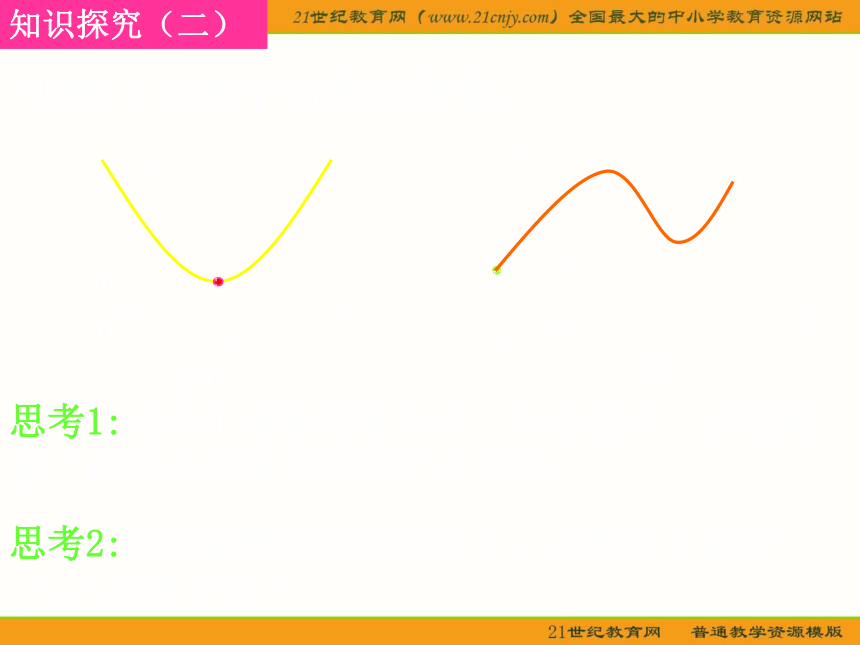
知识探究(二)
观察下列两个函数的图象:
x
y
o
x0
图2
m
思考1:这两个函数图象各有一个最低点,函数图
象上最低点的纵坐标叫什么名称?
思考2:仿照函数最大值的定义,怎样定义函数
的最小值?
一般地,设函数 的定义域为I,如果存在实数m满足:
(1)对于任意的 , 都有 ;
(2)存在 ,使得 .
那么称m是函数 的最小值,记作
知识探究(三)
思考1:如果在函数 定义域内存在x1和 x2,
使对定义域内任意x都有
成立,由此你能得到什么结论?
思考2:对一个函数就最大值和最小值的存在性而
言,有哪几种可能情况?
思考3:如果函数 存在最大值,那么有几个?
思考4:如果函数 的最大值是b,最小值是a,
那么函数 的值域是[a,b]吗?
理论迁移
例1已知函数 ,求函数
的最大值和最小值.
例2(05年湖南卷)某公司在甲、乙两地销售一种
品牌车,利润(万元)分别为
和 ,其中x为销售量(辆),若该公司在
这两地共销售15辆车,则能获得的最大利润为( )
A、45.6万元 B、45.606万元
C、45.56 万元 D、45.51万元
A
例3 设 为常数,如果当 时,函
数 的值域也是[1,b],求b
的值.
4.利用函数的运算性质判断函数的单调性.
若f(x), g(x)为增函数,则有:
f(x)+g(x)为增函数.
f(x).g(x)为增函数. (f(x)>0,g(x)>0)
-f(x) 为减函数.
作业
P39 习题1.3A组:5
B组:1,2.
1.3.1 单调性与最大(小)值
第二课时 函数的最值
问题提出
1.确定函数的单调性有哪些手段和方法?
2.函数图象上升与下降反映了函数的单调性,
如果函数的图象存在最高点或最低点,它又
反映了函数的什么性质?
知识探究(一)
观察下列两个函数的图象:
图1
o
x0
x
M
y
思考1:这两个函数图象有何共同特征?
思考2:设函数y=f(x)图象上最高点的纵坐标为M,
则对函数定义域内任意自变量x,f(x)与M的大小
关系如何?
y
x
o
x0
图2
M
函数图象上最高点的纵坐标叫什么名称?
思考3:设函数 ,则 成立吗?
的最大值是2吗?为什么?
思考4:怎样定义函数 的最大值?用什么符号
表示?
一般地,设函数 的定义域为I,如果存在
实数M满足:
(1)对于任意的 , 都有 ;
(2)存在 ,使得 .
那么称M是函数 的最大值,记作
思考5:函数的最大值是函数值域中的一个元
素吗?如果函数 的值域是(a,b),则函
数 存在最大值吗?
思考6:函数 有最大
值吗?为什么?
图1
y
o
x0
x
m
知识探究(二)
观察下列两个函数的图象:
x
y
o
x0
图2
m
思考1:这两个函数图象各有一个最低点,函数图
象上最低点的纵坐标叫什么名称?
思考2:仿照函数最大值的定义,怎样定义函数
的最小值?
一般地,设函数 的定义域为I,如果存在实数m满足:
(1)对于任意的 , 都有 ;
(2)存在 ,使得 .
那么称m是函数 的最小值,记作
知识探究(三)
思考1:如果在函数 定义域内存在x1和 x2,
使对定义域内任意x都有
成立,由此你能得到什么结论?
思考2:对一个函数就最大值和最小值的存在性而
言,有哪几种可能情况?
思考3:如果函数 存在最大值,那么有几个?
思考4:如果函数 的最大值是b,最小值是a,
那么函数 的值域是[a,b]吗?
理论迁移
例1已知函数 ,求函数
的最大值和最小值.
例2(05年湖南卷)某公司在甲、乙两地销售一种
品牌车,利润(万元)分别为
和 ,其中x为销售量(辆),若该公司在
这两地共销售15辆车,则能获得的最大利润为( )
A、45.6万元 B、45.606万元
C、45.56 万元 D、45.51万元
A
例3 设 为常数,如果当 时,函
数 的值域也是[1,b],求b
的值.
4.利用函数的运算性质判断函数的单调性.
若f(x), g(x)为增函数,则有:
f(x)+g(x)为增函数.
f(x).g(x)为增函数. (f(x)>0,g(x)>0)
-f(x) 为减函数.
作业
P39 习题1.3A组:5
B组:1,2.
