数学:2.1.2 《指数函数的概念与图象》课件(新人教A版必修1)
文档属性
| 名称 | 数学:2.1.2 《指数函数的概念与图象》课件(新人教A版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 117.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-17 19:44:29 | ||
图片预览








文档简介
(共21张PPT)
问题提出
引例1:据国务院发展研究中心2000年发表的《未来20年我国发展前景分析》判断,未来20年我国GDP(国内生产总值)年平均增长率可望达到7.3%. 设x年后我国的GDP为2000年的y倍,则y与x的函数关系是什么?
引例2.当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.根据此规律,生物体内碳14含量P与死亡年数t之间的关系式为什么?
我们把形如 (a>0且a≠1)的函数叫做指数函数,其中x是自变量.
知识探究(二):指数函数的图象
作 和 的图象.
列表:
回顾:作函数图象的步骤
x …… -2 -1 0 1 2 ……
y = 2x …… 1/4 1/2 1 2 4 ……
…… 4 2 1 1/2 1/4 ……
y
x
0
1
2
3
4
1
2
-1
-2
思考1:指数函数y=ax(a>0且a≠1)的值域是什么?
思考2:函数 与 的图象有
什么关系?
y
x
0
1
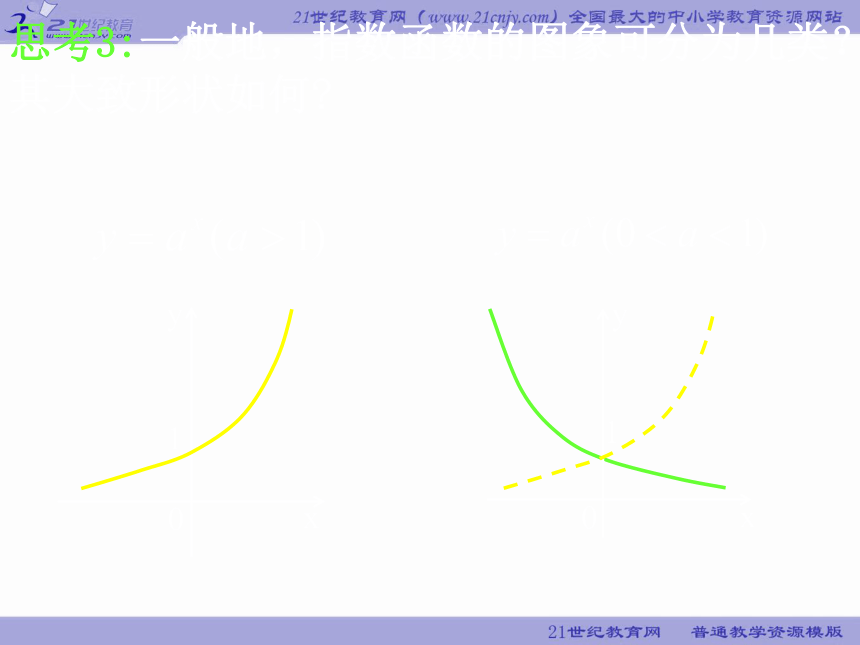
思考3:一般地,指数函数的图象可分为几类?其大致形状如何
x
y
0
1
指数函数y=ax(a>0,且a≠1)的图象和性质:
01
图象
定义域
值域
性质
知识归纳
y
x
0
1
x
y
0
1
R
R
当x>0时0当x<0时y>1;
当x=0时y=1;
在R上是减函数
当x>0时y>1;
当x<0时0当x=0时y=1;
在R上是增函数
理论迁移
例2 已知函数 的图象过点(3,),求 的值.
例1 比较下列各题中两个值的大小
(1) 1.72.5 与 1.73 ;
(2) 0.8-0.1 与 0.8-0.2 ;
(3) 1.70.3 与 0.93.1
例3 求下列函数的定义域和值域;
(1) ;(2) .
例4 若x1、x2为方程
的两个实数解,x1+x2=________.
理论迁移
例5 若指数函数y=(2a-1)x是减函数,求实数a的取值范围.
例6 已知函数
(1)确定f(x)的奇偶性;
(2)判断f(x)的单调性;
(3)求f(x)的值域.
作业
P58练习:2,3.
P59习题2.1A组:5,6.
指数函数y=ax(a>0,且a≠1)的图象和性质:
01
图象
定义域
值域
性质
复习回顾
y
x
0
1
x
y
0
1
R
R
当x>0时0当x<0时y>1;
当x=0时y=1;
在R上是减函数
当x>0时y>1;
当x<0时0当x=0时y=1;
在R上是增函数
y
x
0
1
若a>b>1,则函数 与 的图象的相对位置关系如何?
x
y
0
1
若0如图,指数函数
的图象,则a、b、c、d与1的关系是 ( )
y
x
0
1
A、aB、bC、1D、a1
思考:
1、指数函数具有奇偶性吗?
2、指数函数存在最大值和最小值吗?
讨论:设a>0,a≠1,若am=an,则m与n的大小关系如何?若am>an ,则m与n的大小关系如何?
例3 求函数 的单调区间,
并指出其单调性.
作业
P59习题2.1A组:7,8,9.
问题提出
引例1:据国务院发展研究中心2000年发表的《未来20年我国发展前景分析》判断,未来20年我国GDP(国内生产总值)年平均增长率可望达到7.3%. 设x年后我国的GDP为2000年的y倍,则y与x的函数关系是什么?
引例2.当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.根据此规律,生物体内碳14含量P与死亡年数t之间的关系式为什么?
我们把形如 (a>0且a≠1)的函数叫做指数函数,其中x是自变量.
知识探究(二):指数函数的图象
作 和 的图象.
列表:
回顾:作函数图象的步骤
x …… -2 -1 0 1 2 ……
y = 2x …… 1/4 1/2 1 2 4 ……
…… 4 2 1 1/2 1/4 ……
y
x
0
1
2
3
4
1
2
-1
-2
思考1:指数函数y=ax(a>0且a≠1)的值域是什么?
思考2:函数 与 的图象有
什么关系?
y
x
0
1
思考3:一般地,指数函数的图象可分为几类?其大致形状如何
x
y
0
1
指数函数y=ax(a>0,且a≠1)的图象和性质:
0
图象
定义域
值域
性质
知识归纳
y
x
0
1
x
y
0
1
R
R
当x>0时0
当x=0时y=1;
在R上是减函数
当x>0时y>1;
当x<0时0
在R上是增函数
理论迁移
例2 已知函数 的图象过点(3,),求 的值.
例1 比较下列各题中两个值的大小
(1) 1.72.5 与 1.73 ;
(2) 0.8-0.1 与 0.8-0.2 ;
(3) 1.70.3 与 0.93.1
例3 求下列函数的定义域和值域;
(1) ;(2) .
例4 若x1、x2为方程
的两个实数解,x1+x2=________.
理论迁移
例5 若指数函数y=(2a-1)x是减函数,求实数a的取值范围.
例6 已知函数
(1)确定f(x)的奇偶性;
(2)判断f(x)的单调性;
(3)求f(x)的值域.
作业
P58练习:2,3.
P59习题2.1A组:5,6.
指数函数y=ax(a>0,且a≠1)的图象和性质:
0
图象
定义域
值域
性质
复习回顾
y
x
0
1
x
y
0
1
R
R
当x>0时0
当x=0时y=1;
在R上是减函数
当x>0时y>1;
当x<0时0
在R上是增函数
y
x
0
1
若a>b>1,则函数 与 的图象的相对位置关系如何?
x
y
0
1
若0
的图象,则a、b、c、d与1的关系是 ( )
y
x
0
1
A、a
思考:
1、指数函数具有奇偶性吗?
2、指数函数存在最大值和最小值吗?
讨论:设a>0,a≠1,若am=an,则m与n的大小关系如何?若am>an ,则m与n的大小关系如何?
例3 求函数 的单调区间,
并指出其单调性.
作业
P59习题2.1A组:7,8,9.
