数学:2.2.2《对数函数及其性质》课件(新人教A版必修1)
文档属性
| 名称 | 数学:2.2.2《对数函数及其性质》课件(新人教A版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 150.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-17 00:00:00 | ||
图片预览


文档简介
(共9张PPT)
2.2.2对数函数及其性质(3)
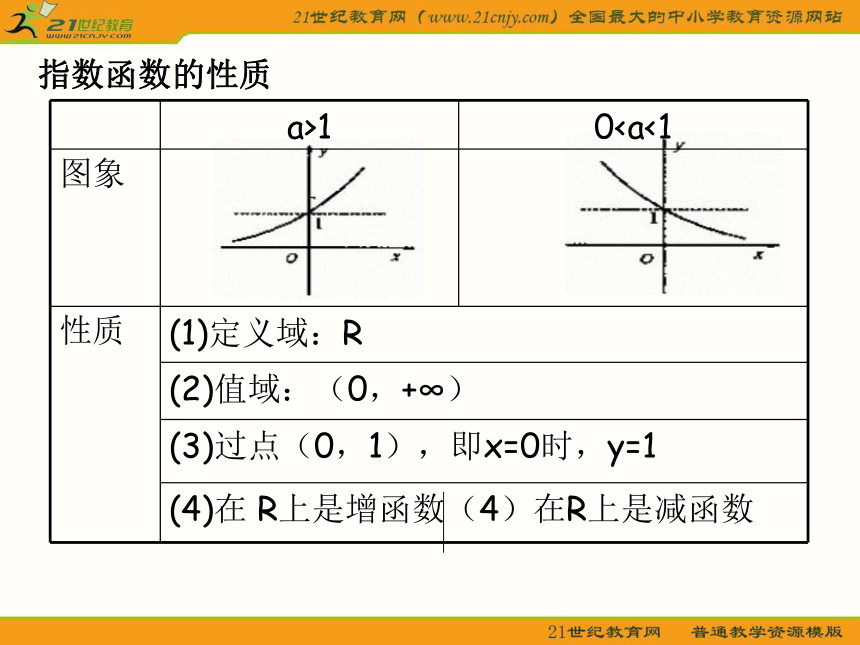
a>1 0图象
性质 (1)定义域:R
(2)值域:(0,+∞)
(3)过点(0,1),即x=0时,y=1
(4)在 R上是增函数(4)在R上是减函数
指数函数的性质
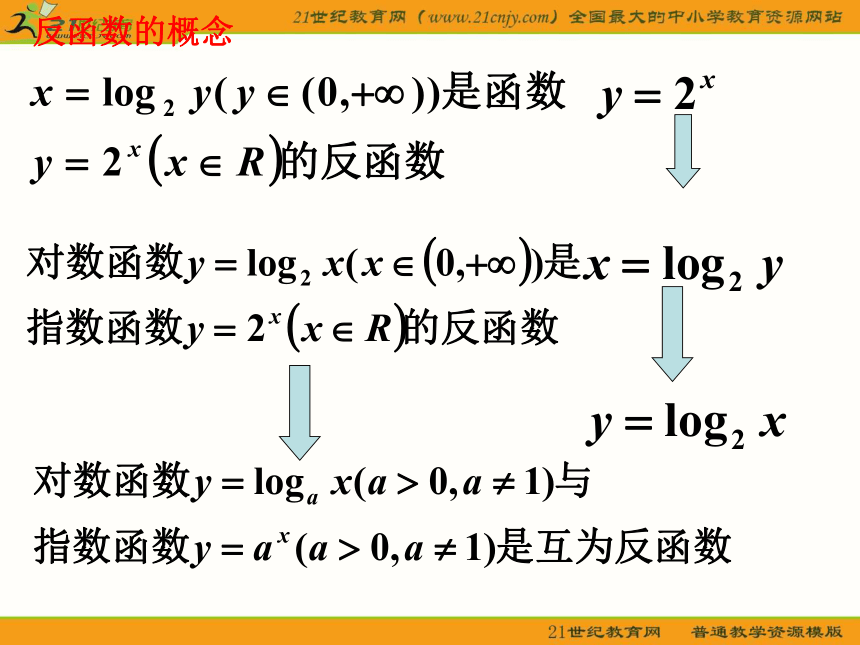
反函数的概念
设A,B分别为函数y=f(x)的定义域和值域,如果由函数y=f(x)所解得 也是一个函数(即对任意一个 ,都有唯一的 与之对应),那么就称函数 是函数y=f(x)的反函数,记作: 。习惯上,用x表示自变量,y表示函数,因此的反函数 通常改写成:
二 反函数的概念
注.y=f(x)的定义域、值域分别是反函数
的值域、定义域
例3 求下列函数的反函数
(2)y=log2(4-x) (x<4)
(1)y=0.2-x+1
对数函数与指数函数的图象
由于对数函数
与指数函数
互为反函数,
所以
的图象与
的图象关于直线
对称。
思考.已知函数
(1)当定义域为R时,求a的取值范围;
(2)当值域为R时,求a的取值范围.
小结:
1.指数函数与对数函数的关系.
2.反函数的定义和图象的特点.
2.已知 是R上的奇
函数,(1)求a的值;(2)求f(x)的反函数;
练习:
2.2.2对数函数及其性质(3)
a>1 0
性质 (1)定义域:R
(2)值域:(0,+∞)
(3)过点(0,1),即x=0时,y=1
(4)在 R上是增函数(4)在R上是减函数
指数函数的性质
反函数的概念
设A,B分别为函数y=f(x)的定义域和值域,如果由函数y=f(x)所解得 也是一个函数(即对任意一个 ,都有唯一的 与之对应),那么就称函数 是函数y=f(x)的反函数,记作: 。习惯上,用x表示自变量,y表示函数,因此的反函数 通常改写成:
二 反函数的概念
注.y=f(x)的定义域、值域分别是反函数
的值域、定义域
例3 求下列函数的反函数
(2)y=log2(4-x) (x<4)
(1)y=0.2-x+1
对数函数与指数函数的图象
由于对数函数
与指数函数
互为反函数,
所以
的图象与
的图象关于直线
对称。
思考.已知函数
(1)当定义域为R时,求a的取值范围;
(2)当值域为R时,求a的取值范围.
小结:
1.指数函数与对数函数的关系.
2.反函数的定义和图象的特点.
2.已知 是R上的奇
函数,(1)求a的值;(2)求f(x)的反函数;
练习:
