数学:2.2《对数函数》课件(新人教A版必修1)
文档属性
| 名称 | 数学:2.2《对数函数》课件(新人教A版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 115.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-17 19:44:29 | ||
图片预览





文档简介
(共20张PPT)
2001年10月23日
学习目标:
1、理解对数函数的概念;
2、掌握对数函数的图象和性质;
3、数形结合意识的继续加强。
重点、难点:
重点是对数函数的图象和性质;
难点是对数函数与指数函数的联系。
一、前提诊测:
1、对数的定义:
2、求函数y=2x+1的反函数。
3、互为反函数的两个函数的图象有什么关系?
关于直线y=x对称
一般地,若ab=N(a>0,a≠1),则数b就叫做以a为底N的对数,记做logaN=b
二、对数函数的引入:
问题1:某种细胞分裂时,由1个分裂为2个,2个分裂为4个……1个这样的细胞分裂x次后,得到的细胞个数设为y,则y与x的函数关系式为:
Y=2x
问题2:某种细胞分裂时,由1个分裂为2个,2个分裂为4个……如果要求这种细胞经过多少次分裂,大约可以得到1万个,10万个……细胞,那么分裂次数x就是要得到的细胞个数y的函数。由对数的定义,这个函数可以写成:
X=log2y
变化过程:
Y=2x
X=log2y
Y=log2x
结论:函数y=log2x和指数函数y=2x互为反函数
三、对数函数的定义:
函数y=logax(a>0,a≠1)叫做对数函数
需注意的几点:
①对数函数y=logax和指数函数y=ax互为反函数
②对数函数的解析式可由指数函数求反函数得到
③对数函数的定义域、值域也就是指数函数的 值域、定义域
想一想:对数函数的定义域和值域分别是什么?
因为指数函数的定义域是R 值域是(0,+∞)
所以对数函数的定义域是(0,+∞) 值域是R
四、对数函数的图象和性质
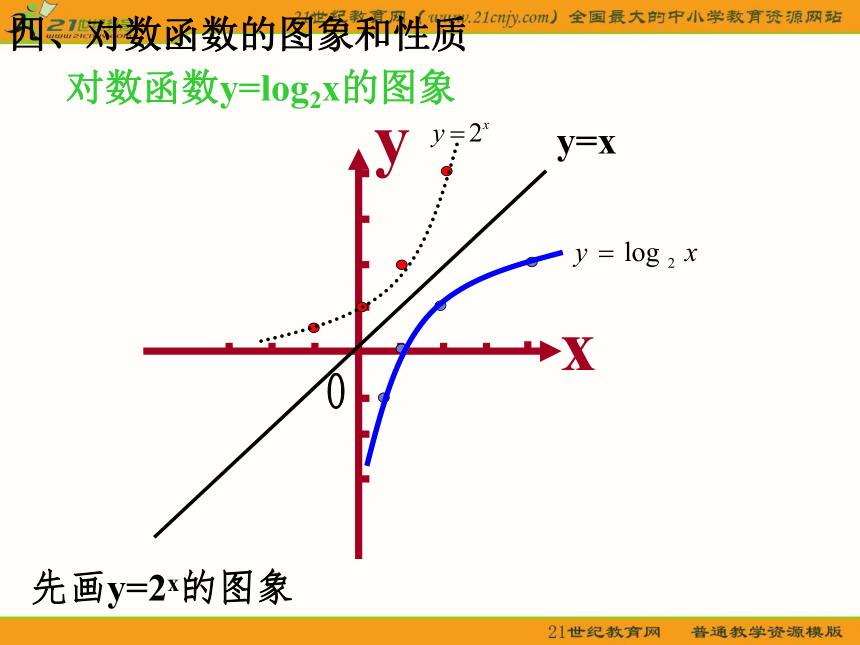
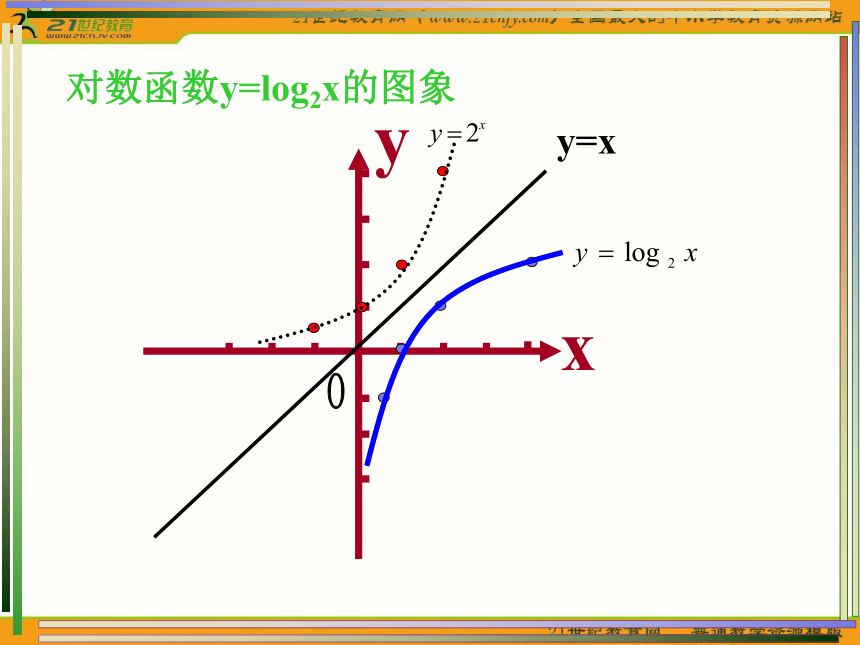
对数函数y=log2x的图象
x
y
y=x
先画y=2x的图象
对数函数y=log2x的图象
x
y
y=x
x
y
四、对数函数的图象和性质
对数函数y=log x的图象
y=x
y=log x
先画 的图象
x
y
对数函数y=log x的图象
y=x
y=log x
y=logax(a>1)的图象
y=logax(0一般地,对数函数y=logax在a>1及0
a>1 0<a<1
图
象
性
质 ⑴定义域:
⑵值域:
⑶过特殊点:
⑷单调性 : ⑷单调性:
(0,+∞)
R
过点(1,0),即x=1时y=0
在(0,+∞)上是增函数
在(0,+∞)上是减函数
当0<x<1时,y<0
当x=1时,y=0
当x>1时,y>0
当0<x<1时,y>0
当x=1时,y=0
当x>1时,y<0
五、应用举例:
例1:求下列函数的定义域:
①y=logax2 ②y=loga(4-x) ③y=loga(9-x2)
分析:此题主要利用对数函数y=logax的定义域为(0,+∞)求解。
①因为x2 >0,即x≠0,
所以函数y=logax2 的定义域是{x│x≠0}
②因为4-x>0,即x<4,
所以函数y=loga(4-x)的定义域是{x│x<4}
③因为9-x2>0,即-3所以函数y=loga(9-x2)的定义域是{x│-3解:
六、课堂练习:
y=log3x
y=log x
1、画出函数y=log3x及y=log x的图象,并且
说明这两个函数的相同性质和不同性质。
y=log x
y=log3x
六、课堂练习:
1、画出函数y=log3x及y=log x的图象,并且
说明这两个函数的相同性质和不同性质。
相同性质:都位于y轴右方,都经过点(1,0),这说明这两个函数的定义域都是(0,+∞),且x=1时y=0
不同性质:y=log3x的图象是上升的曲线,y=log x的图象是下降的曲线,这说明前者在(0,+∞)是增函数,后者在(0,+∞)是减函数。
⑴
⑵
⑶
⑷
⑴因为1-x>0,即x<1,
所以函数 的定义域为{x∣x<1}
⑵因为x>0且 ≠0
所以函数 的定义域为{x∣0<x<1,或x>1}
⑶因为 >0,即x<
所以函数 的定义域为{x∣x< }
⑷因为x>0且 ≥0
所以函数 的定义域为{x∣x≥1}
2、求下列函数的定义域:
解:
通过本节课的学习,大家应逐步掌握对数函数的图象和性质,并能利用对数函数的性质解决一些简单问题,如求对数形式的复合函数的定义域问题。
1预习内容: 预习提纲:①同底数的两个对数如何比较大小?
②不同底数的两个对数如何比较大小?
2挑战自己:
你能否尽可能完整地总结出指数函数和对数函数的区别和联系?请试一试。
谢谢大家!
2001年10月23日
学习目标:
1、理解对数函数的概念;
2、掌握对数函数的图象和性质;
3、数形结合意识的继续加强。
重点、难点:
重点是对数函数的图象和性质;
难点是对数函数与指数函数的联系。
一、前提诊测:
1、对数的定义:
2、求函数y=2x+1的反函数。
3、互为反函数的两个函数的图象有什么关系?
关于直线y=x对称
一般地,若ab=N(a>0,a≠1),则数b就叫做以a为底N的对数,记做logaN=b
二、对数函数的引入:
问题1:某种细胞分裂时,由1个分裂为2个,2个分裂为4个……1个这样的细胞分裂x次后,得到的细胞个数设为y,则y与x的函数关系式为:
Y=2x
问题2:某种细胞分裂时,由1个分裂为2个,2个分裂为4个……如果要求这种细胞经过多少次分裂,大约可以得到1万个,10万个……细胞,那么分裂次数x就是要得到的细胞个数y的函数。由对数的定义,这个函数可以写成:
X=log2y
变化过程:
Y=2x
X=log2y
Y=log2x
结论:函数y=log2x和指数函数y=2x互为反函数
三、对数函数的定义:
函数y=logax(a>0,a≠1)叫做对数函数
需注意的几点:
①对数函数y=logax和指数函数y=ax互为反函数
②对数函数的解析式可由指数函数求反函数得到
③对数函数的定义域、值域也就是指数函数的 值域、定义域
想一想:对数函数的定义域和值域分别是什么?
因为指数函数的定义域是R 值域是(0,+∞)
所以对数函数的定义域是(0,+∞) 值域是R
四、对数函数的图象和性质
对数函数y=log2x的图象
x
y
y=x
先画y=2x的图象
对数函数y=log2x的图象
x
y
y=x
x
y
四、对数函数的图象和性质
对数函数y=log x的图象
y=x
y=log x
先画 的图象
x
y
对数函数y=log x的图象
y=x
y=log x
y=logax(a>1)的图象
y=logax(0
a>1 0<a<1
图
象
性
质 ⑴定义域:
⑵值域:
⑶过特殊点:
⑷单调性 : ⑷单调性:
(0,+∞)
R
过点(1,0),即x=1时y=0
在(0,+∞)上是增函数
在(0,+∞)上是减函数
当0<x<1时,y<0
当x=1时,y=0
当x>1时,y>0
当0<x<1时,y>0
当x=1时,y=0
当x>1时,y<0
五、应用举例:
例1:求下列函数的定义域:
①y=logax2 ②y=loga(4-x) ③y=loga(9-x2)
分析:此题主要利用对数函数y=logax的定义域为(0,+∞)求解。
①因为x2 >0,即x≠0,
所以函数y=logax2 的定义域是{x│x≠0}
②因为4-x>0,即x<4,
所以函数y=loga(4-x)的定义域是{x│x<4}
③因为9-x2>0,即-3
六、课堂练习:
y=log3x
y=log x
1、画出函数y=log3x及y=log x的图象,并且
说明这两个函数的相同性质和不同性质。
y=log x
y=log3x
六、课堂练习:
1、画出函数y=log3x及y=log x的图象,并且
说明这两个函数的相同性质和不同性质。
相同性质:都位于y轴右方,都经过点(1,0),这说明这两个函数的定义域都是(0,+∞),且x=1时y=0
不同性质:y=log3x的图象是上升的曲线,y=log x的图象是下降的曲线,这说明前者在(0,+∞)是增函数,后者在(0,+∞)是减函数。
⑴
⑵
⑶
⑷
⑴因为1-x>0,即x<1,
所以函数 的定义域为{x∣x<1}
⑵因为x>0且 ≠0
所以函数 的定义域为{x∣0<x<1,或x>1}
⑶因为 >0,即x<
所以函数 的定义域为{x∣x< }
⑷因为x>0且 ≥0
所以函数 的定义域为{x∣x≥1}
2、求下列函数的定义域:
解:
通过本节课的学习,大家应逐步掌握对数函数的图象和性质,并能利用对数函数的性质解决一些简单问题,如求对数形式的复合函数的定义域问题。
1预习内容: 预习提纲:①同底数的两个对数如何比较大小?
②不同底数的两个对数如何比较大小?
2挑战自己:
你能否尽可能完整地总结出指数函数和对数函数的区别和联系?请试一试。
谢谢大家!
