数学:第二章《基本初等函数》章综合(新人教A版必修1)
文档属性
| 名称 | 数学:第二章《基本初等函数》章综合(新人教A版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 84.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-17 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
必修1函数复习
根据图象确定系数取值范围
一次函数 (k≠0)
反比例函数 (k≠0)
二次函数 (a≠0)
一次函数
一条直线
K>0时,y随x的增大而增大
k<0时,y随x的增大而减小
图象:
性质:
定义:
y=kx+b(k≠0)
例题:根据一次函数图象确定
字母系数取值范围
y=kx+b
(1)
y=kx+b
(2)
k>0
b>0
k<0
b<0
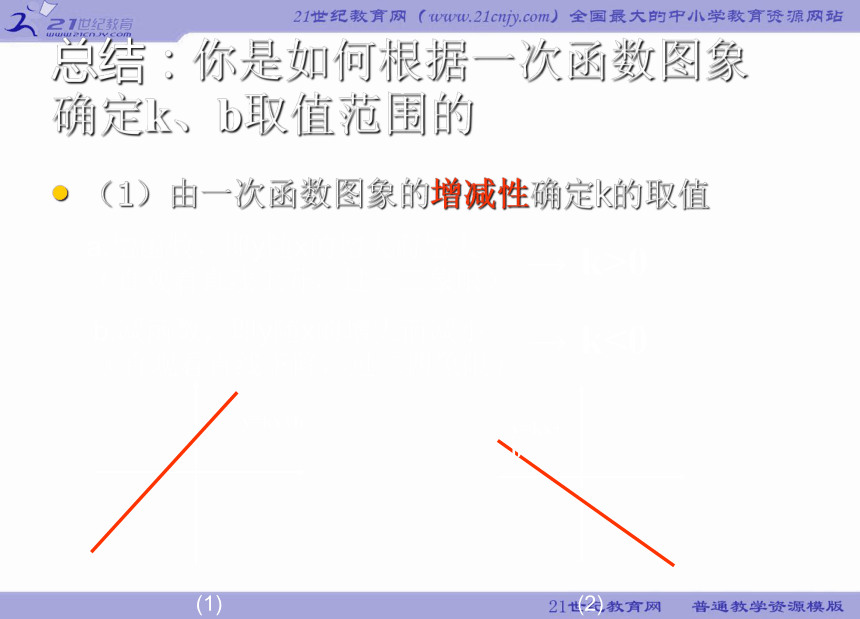
总结:你是如何根据一次函数图象
确定k、b取值范围的
(1)由一次函数图象的增减性确定k的取值
a.增函数,即y随x的增大而增大
(直观看直线上升,过一三象限)
→ k>0
b.减函数,即y随x的增大而减小
(直观看直线下降,过二四象限)
→ k<0
y=kx+b
(1)
y=kx+b
(2)
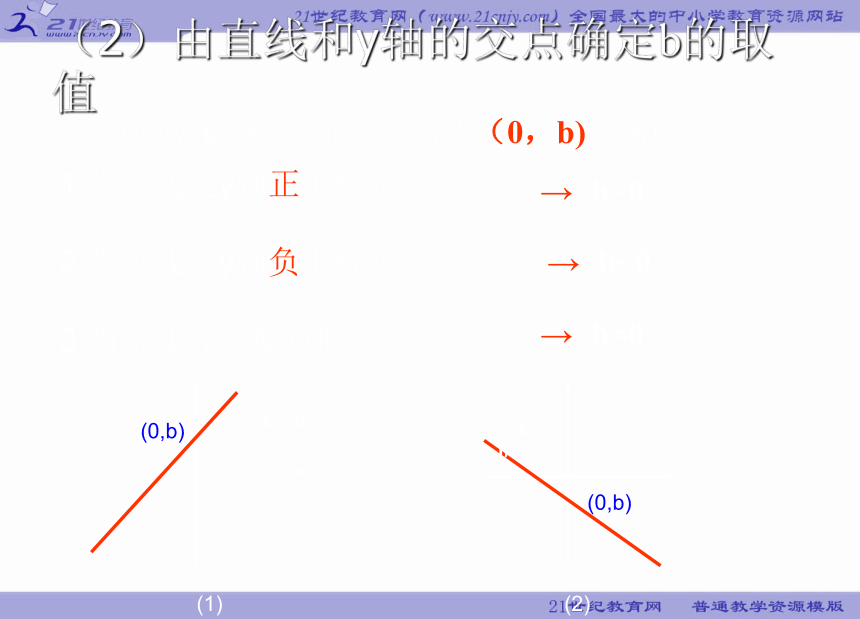
(2)由直线和y轴的交点确定b的取值
因为直线y=kx+b与y轴交点坐标为(0,b) ,所以
1.当直线交y轴正半轴时
→ b>0
2.当直线交y轴负半轴时
→ b<0
(0,b)
y=kx+b
(1)
y=kx+b
(2)
(0,b)
3.当直线经过原点时
→ b=0
根据你所学知识,确定下列一次函数中字母系数的取值范围
y=kx+b
y=kx+b
(1)
O
y
x
(2)
O
y
x
y=(5-a)x+c+3
y=-ax-b
根据你所学知识,确定下列一次函数中字母系数的取值范围
y=(5-a)x+b+3
y=(k-2)x-b
(3)
(4)
O
x
x
y
y
O
反比例函数
定义:
图象:
双曲线
性质:
k>0时,图象在一三象限,在每个象限内,y随x的增大而减小。
k<0时,图象在二四象限,在每个象限内,y随x的增大而增大。
(k≠0)
二次函数
定义:
图象:
性质:
(a≠0)
抛物线
(1)当a>0时,抛物线开口向上;
当a<0时,抛物线开口向下。
(2)对称轴:直线
(3)顶点坐标:
如何根据二次函数图象确定系数取值范围?
1.根据抛物线的开口方向确定a的值
开口向上----a>0 ; 开口向下----a<0
2.根据对称轴的位置确定b的取值
对称轴在y轴左侧
a、b异号
a、b同号
对称轴在y轴右侧
a、b的符号“左同右异”
对称轴是y轴,b=?
如何根据二次函数图象确定系数取值范围?
c的符号确定:
交y轴正半轴
c>0
交y轴负半轴
c<0
经过原点
c=0
与y轴交点为(0,c)
抛物线
综合练习
在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为
O
y
x
O
y
x
O
y
x
O
y
x
A
B
C
D
2004年河北省中考题
已知函数y=k(x+1)和y=k/x,那么它们在同一坐标系中的图象大致位置是
O
y
x
O
y
x
O
y
x
O
y
x
A
B
C
D
函数y=ax+b和y=ax2+bx+c在同一坐标系中的图象可能是
A
B
C
D
O
y
x
O
y
x
O
y
x
O
y
x
必修1函数复习
根据图象确定系数取值范围
一次函数 (k≠0)
反比例函数 (k≠0)
二次函数 (a≠0)
一次函数
一条直线
K>0时,y随x的增大而增大
k<0时,y随x的增大而减小
图象:
性质:
定义:
y=kx+b(k≠0)
例题:根据一次函数图象确定
字母系数取值范围
y=kx+b
(1)
y=kx+b
(2)
k>0
b>0
k<0
b<0
总结:你是如何根据一次函数图象
确定k、b取值范围的
(1)由一次函数图象的增减性确定k的取值
a.增函数,即y随x的增大而增大
(直观看直线上升,过一三象限)
→ k>0
b.减函数,即y随x的增大而减小
(直观看直线下降,过二四象限)
→ k<0
y=kx+b
(1)
y=kx+b
(2)
(2)由直线和y轴的交点确定b的取值
因为直线y=kx+b与y轴交点坐标为(0,b) ,所以
1.当直线交y轴正半轴时
→ b>0
2.当直线交y轴负半轴时
→ b<0
(0,b)
y=kx+b
(1)
y=kx+b
(2)
(0,b)
3.当直线经过原点时
→ b=0
根据你所学知识,确定下列一次函数中字母系数的取值范围
y=kx+b
y=kx+b
(1)
O
y
x
(2)
O
y
x
y=(5-a)x+c+3
y=-ax-b
根据你所学知识,确定下列一次函数中字母系数的取值范围
y=(5-a)x+b+3
y=(k-2)x-b
(3)
(4)
O
x
x
y
y
O
反比例函数
定义:
图象:
双曲线
性质:
k>0时,图象在一三象限,在每个象限内,y随x的增大而减小。
k<0时,图象在二四象限,在每个象限内,y随x的增大而增大。
(k≠0)
二次函数
定义:
图象:
性质:
(a≠0)
抛物线
(1)当a>0时,抛物线开口向上;
当a<0时,抛物线开口向下。
(2)对称轴:直线
(3)顶点坐标:
如何根据二次函数图象确定系数取值范围?
1.根据抛物线的开口方向确定a的值
开口向上----a>0 ; 开口向下----a<0
2.根据对称轴的位置确定b的取值
对称轴在y轴左侧
a、b异号
a、b同号
对称轴在y轴右侧
a、b的符号“左同右异”
对称轴是y轴,b=?
如何根据二次函数图象确定系数取值范围?
c的符号确定:
交y轴正半轴
c>0
交y轴负半轴
c<0
经过原点
c=0
与y轴交点为(0,c)
抛物线
综合练习
在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为
O
y
x
O
y
x
O
y
x
O
y
x
A
B
C
D
2004年河北省中考题
已知函数y=k(x+1)和y=k/x,那么它们在同一坐标系中的图象大致位置是
O
y
x
O
y
x
O
y
x
O
y
x
A
B
C
D
函数y=ax+b和y=ax2+bx+c在同一坐标系中的图象可能是
A
B
C
D
O
y
x
O
y
x
O
y
x
O
y
x
