数学:3.2.1《几类不同增长的函数模型(2)》课件(新人教A版必修1)
文档属性
| 名称 | 数学:3.2.1《几类不同增长的函数模型(2)》课件(新人教A版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 148.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-17 19:44:56 | ||
图片预览



文档简介
(共14张PPT)
函数模型及其应用
3.2.1 几类不同增长的函数模型二
我们知道,对数函数 ,指数函数 与幂函数 在区间 上都是增函数。从上述两个例子可以看到,这三类函数的增长是有差异的。那么,这种差异的具体情况到底怎样呢?
下面,我们不妨先以
函数为例进行探究。
利用计算器或计算机,以一定的步长列出自变量与函数值的对应表(表3-5)
,并在同一平面直角坐标系内画出三个函数的图象(图3.2-4)。可以看到,虽然它们都是增函数,但它们的增长速度是不同的。
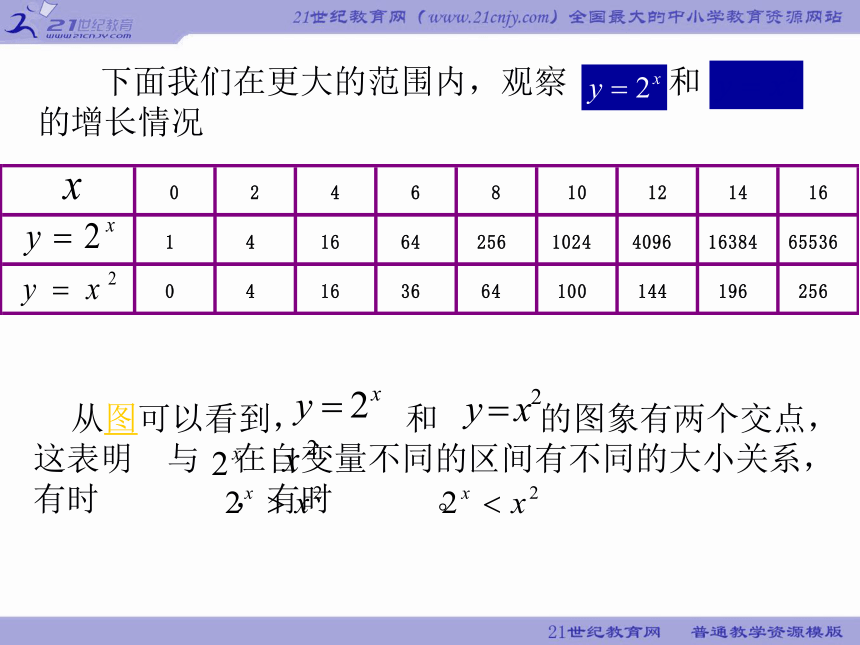
表3-5
从图可以看到, 和 的图象有两个交点,这表明 与 在自变量不同的区间有不同的大小关系,有时 ,有时 。
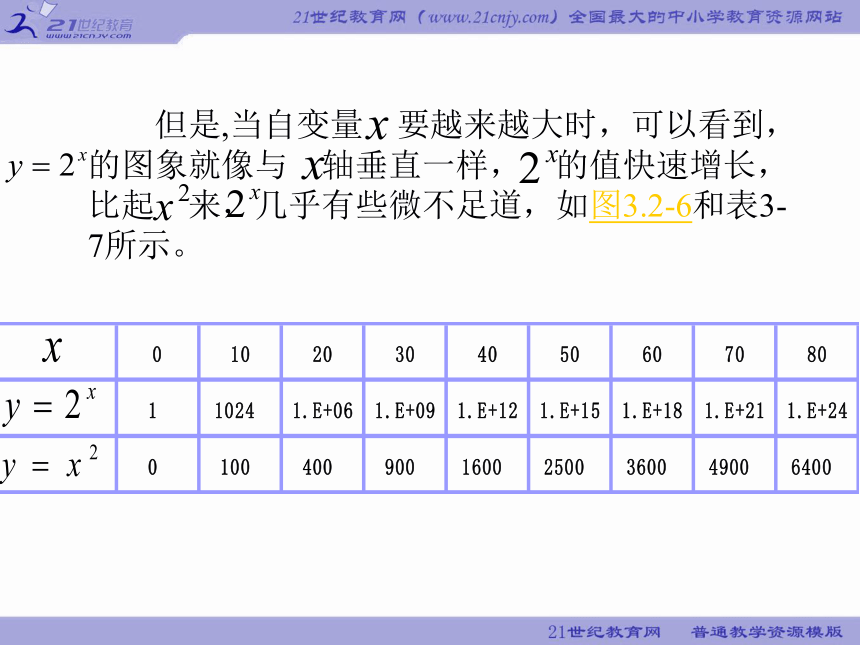
下面我们在更大的范围内,观察 和 的增长情况
但是,当自变量 要越来越大时,可以看到, 的图象就像与 轴垂直一样, 的值快速增长, 比起 来,几乎有些微不足道,如图3.2-6和表3-7所示。
探究
你能借助图象,对 和 的增长情况进行比较吗?
请在图象上分别标出使不等式
成立的自变量 的取值范围
结论
一般地,对于指数函数 和幂函数 ,通过探索可以发现,在区间 上,无论 比 大多少,尽管在 的一定变化范围内, 会小于 ,由于 的增长快于 的增长,因此总存在一个 ,当 时,就会有 。
同样地,对于对数函数 和幂函数 , 在区间 上,随着 的增大, 增长得越来越慢,图象就像是渐渐地与 轴平行一样,尽管在 的一定变化范围内, 可能会大于 ,但由于 的增长慢于 的增长,因此总存在一个 ,当 时,就会有 。
综上所述,在区间 上,尽 管 函 数 、 、 和 都是增函数,但它们的增长速度不同,而且不在同一个“档次”上。随着 的增大, 的增长速度越来越快,会超过并远远大于 的增长速度,
而 的增长速度则会越来越慢。因此,总会存在一个 , 当 时,就有
。
探究
你能用同样的方法,讨论一下函数:
、 、
在区间 上的衰减情况吗?
练习P119
在同一个平面直角坐标系内作出下列函数的图象,并比较它们的增长情况:
函数模型及其应用
3.2.1 几类不同增长的函数模型二
我们知道,对数函数 ,指数函数 与幂函数 在区间 上都是增函数。从上述两个例子可以看到,这三类函数的增长是有差异的。那么,这种差异的具体情况到底怎样呢?
下面,我们不妨先以
函数为例进行探究。
利用计算器或计算机,以一定的步长列出自变量与函数值的对应表(表3-5)
,并在同一平面直角坐标系内画出三个函数的图象(图3.2-4)。可以看到,虽然它们都是增函数,但它们的增长速度是不同的。
表3-5
从图可以看到, 和 的图象有两个交点,这表明 与 在自变量不同的区间有不同的大小关系,有时 ,有时 。
下面我们在更大的范围内,观察 和 的增长情况
但是,当自变量 要越来越大时,可以看到, 的图象就像与 轴垂直一样, 的值快速增长, 比起 来,几乎有些微不足道,如图3.2-6和表3-7所示。
探究
你能借助图象,对 和 的增长情况进行比较吗?
请在图象上分别标出使不等式
成立的自变量 的取值范围
结论
一般地,对于指数函数 和幂函数 ,通过探索可以发现,在区间 上,无论 比 大多少,尽管在 的一定变化范围内, 会小于 ,由于 的增长快于 的增长,因此总存在一个 ,当 时,就会有 。
同样地,对于对数函数 和幂函数 , 在区间 上,随着 的增大, 增长得越来越慢,图象就像是渐渐地与 轴平行一样,尽管在 的一定变化范围内, 可能会大于 ,但由于 的增长慢于 的增长,因此总存在一个 ,当 时,就会有 。
综上所述,在区间 上,尽 管 函 数 、 、 和 都是增函数,但它们的增长速度不同,而且不在同一个“档次”上。随着 的增大, 的增长速度越来越快,会超过并远远大于 的增长速度,
而 的增长速度则会越来越慢。因此,总会存在一个 , 当 时,就有
。
探究
你能用同样的方法,讨论一下函数:
、 、
在区间 上的衰减情况吗?
练习P119
在同一个平面直角坐标系内作出下列函数的图象,并比较它们的增长情况:
