数学:第三章《函数的应用》复习课件(新人教A版必修1)
文档属性
| 名称 | 数学:第三章《函数的应用》复习课件(新人教A版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 301.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-17 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
业精于勤,荒于嬉,行成于思,毁于随。
学 而 不 思 则 罔, 思 而 不 学 则 殆。
成绩=勤奋的学习+正确的方法+少谈空话
博学之,审问之,慎思之,明辨之,笃行之。
自觉、自 律、自信、自 强 !
第三章 函数的应用
复习课
一、本章知识框架
二分法求方程近似解
函数与方程
方程的根与函数的零点
几类不同增长的函数模型
函数模型
及其应用
用已知函数模型解决问题
构建函数模型解决问题
4、判断是否达到精确度ε :
若︱a-b︱<ε,则达到了精确度,取区间端点之一为零点的近似值即告结束;否则,重复2-4的工作。
Ⅰ.用二分法求函数f(x)零点近似值(精确度ε)的步骤:
1.选取满足条件 的实数a,b(一般取整数) , 确定区间[a,b];
2.求区间 (a,b)的中点 ,记为c ;
3.计算f(c),并进行判断:
(1)若f(c) =0,则c 就是函数的零点,结束;
(2)若 ,则 ,令b=c,转向4;
(3)若 ,则 ,令a=c,转向4;
二、主要知识点与方法
Ⅱ.指数函数、对数函数、幂函数、一次函数这四种函数模型的增长差异。
答:指数(底数大于1)爆炸增长
幂函数(幂指数大于1)快速增长
直线(一次项系数为正)匀速增长
对数(底数大于1)缓慢增长
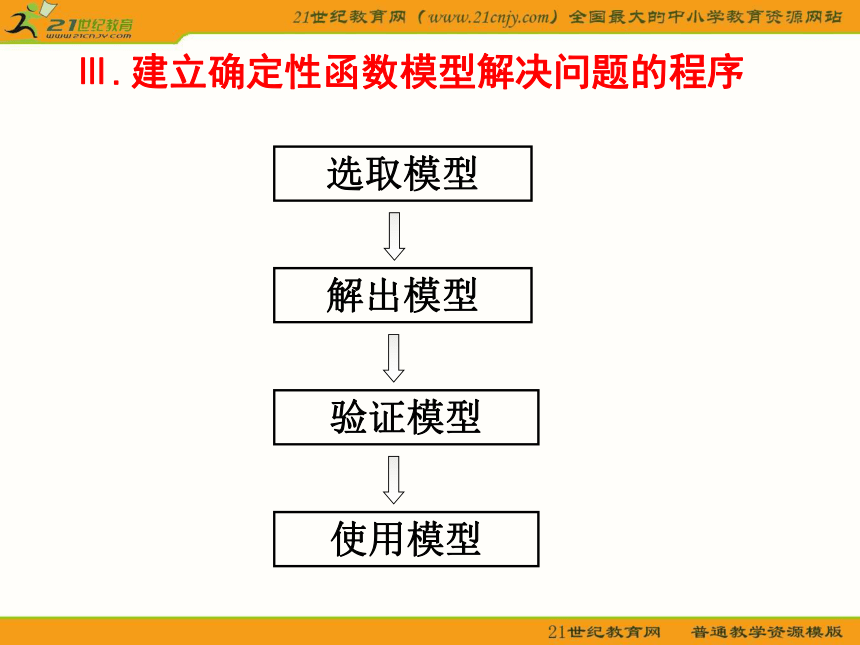
解出模型
验证模型
使用模型
选取模型
Ⅲ.建立确定性函数模型解决问题的程序
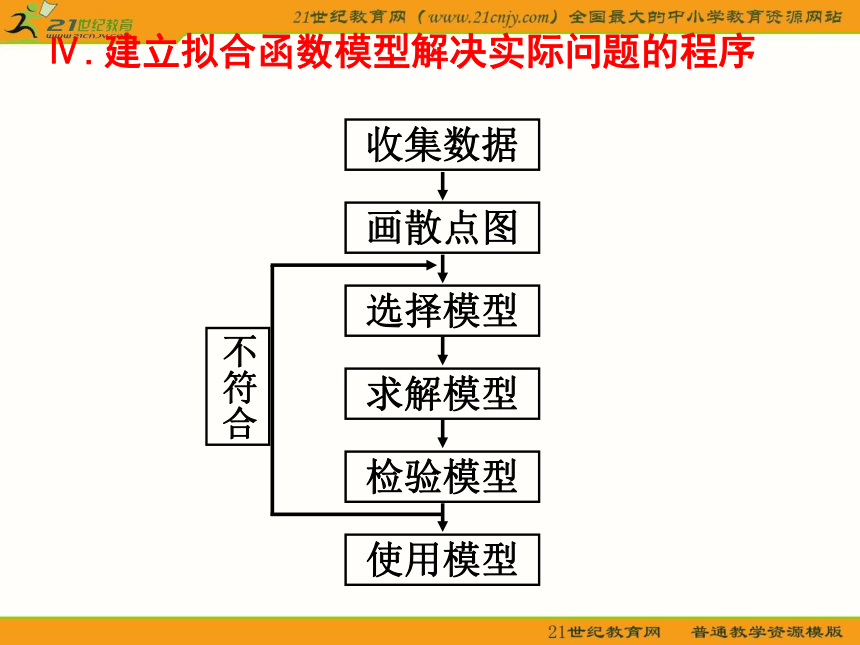
收集数据
画散点图
选择模型
求解模型
检验模型
使用模型
不符合
Ⅳ.建立拟合函数模型解决实际问题的程序
1.若函数y=f(x)唯一的一个零点在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题正确的是( )
(A)函数y=f(x) 在区间(0,1)内有零点
(B)函数y=f(x) 在区间(0,1)或(1,2)内有零点
(C)函数y=f(x) 在区间 [2,16] 内无零点
(D)函数y=f(x) 在区间(1,16)内无零点
C
三、复习参考题
5.用二分法求方程 的最大的根(精确度0.01) .
x
-3
-2
-1
0
1
2
3
f(x)符号
-
-
-
+
-
-
+
分析:设f(x)= 通过计算得到:
可见方程的根分别落在区间(-1,0),(0,1)和(2,3)内,而最大的根落在区间(2,3)内.
然后利用二分法在区间(2,3)内求出符合精确度要求的方程近似解x=2.5234375
5.用二分法求方程 的最大的根(精确度0.01) .
9.某公司每生产一批产品都能维持一段时间的市场供应.若该公司本次新产品生产开始x月后,公司的存货量大致满足模型f(x)=-3x3+12x+8
那么下次生产应在多长时间后开始?
分析: 只要求出比函数f(x) 最小的正零点小的正数.
解:因为f(0)>0,f(1)>0, f(2)>0, f(3)<0,
所以下次生产应在2个月后开始.
2. 点P从点O出发,按逆时针方向沿周长为l 的图形运动一周,O,P两点连线的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是 ( )
l
x
y
o
o
P
A
o
P
B
o
P
C
o
P
D
C
4. 设计四个杯子的形状,使得在向杯中匀速注水时,杯中水面的高度h随时间t变化的图象分别与下列图象相符合.
t
h
o
图(1)
t
h
o
图(2)
t
h
o
图(3)
t
h
o
图(4)
t
h
o
图(4)
3.列车从A地出发直达500km以外的B地,途中要经过离A地200km的C地。假设列车匀速前进,试画出列车与C地的距离s关于时间t的函数图象。
0
T
200
t
s
500
0.4T
解:设列车从A地到B地所用时间为T.
则当t=0时s=200;
当t=0.4T时s=0;
当t=T时s=500.
因为列车匀速行驶,所以距离s是时间t的一次函数,
B组 2:如图,△OAB是
边长为2的正三角形,记
△OAB位于直线x=t(t>0)
左侧的图形的面积为f(t).
试求函数f(t)的解析式,
并画出函数y=f(t)的图象.
0
A
B
x
y
x=t
{
解: y=f(t)=
业精于勤,荒于嬉,行成于思,毁于随。
学 而 不 思 则 罔, 思 而 不 学 则 殆。
成绩=勤奋的学习+正确的方法+少谈空话
博学之,审问之,慎思之,明辨之,笃行之。
自觉、自 律、自信、自 强 !
第三章 函数的应用
复习课
一、本章知识框架
二分法求方程近似解
函数与方程
方程的根与函数的零点
几类不同增长的函数模型
函数模型
及其应用
用已知函数模型解决问题
构建函数模型解决问题
4、判断是否达到精确度ε :
若︱a-b︱<ε,则达到了精确度,取区间端点之一为零点的近似值即告结束;否则,重复2-4的工作。
Ⅰ.用二分法求函数f(x)零点近似值(精确度ε)的步骤:
1.选取满足条件 的实数a,b(一般取整数) , 确定区间[a,b];
2.求区间 (a,b)的中点 ,记为c ;
3.计算f(c),并进行判断:
(1)若f(c) =0,则c 就是函数的零点,结束;
(2)若 ,则 ,令b=c,转向4;
(3)若 ,则 ,令a=c,转向4;
二、主要知识点与方法
Ⅱ.指数函数、对数函数、幂函数、一次函数这四种函数模型的增长差异。
答:指数(底数大于1)爆炸增长
幂函数(幂指数大于1)快速增长
直线(一次项系数为正)匀速增长
对数(底数大于1)缓慢增长
解出模型
验证模型
使用模型
选取模型
Ⅲ.建立确定性函数模型解决问题的程序
收集数据
画散点图
选择模型
求解模型
检验模型
使用模型
不符合
Ⅳ.建立拟合函数模型解决实际问题的程序
1.若函数y=f(x)唯一的一个零点在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题正确的是( )
(A)函数y=f(x) 在区间(0,1)内有零点
(B)函数y=f(x) 在区间(0,1)或(1,2)内有零点
(C)函数y=f(x) 在区间 [2,16] 内无零点
(D)函数y=f(x) 在区间(1,16)内无零点
C
三、复习参考题
5.用二分法求方程 的最大的根(精确度0.01) .
x
-3
-2
-1
0
1
2
3
f(x)符号
-
-
-
+
-
-
+
分析:设f(x)= 通过计算得到:
可见方程的根分别落在区间(-1,0),(0,1)和(2,3)内,而最大的根落在区间(2,3)内.
然后利用二分法在区间(2,3)内求出符合精确度要求的方程近似解x=2.5234375
5.用二分法求方程 的最大的根(精确度0.01) .
9.某公司每生产一批产品都能维持一段时间的市场供应.若该公司本次新产品生产开始x月后,公司的存货量大致满足模型f(x)=-3x3+12x+8
那么下次生产应在多长时间后开始?
分析: 只要求出比函数f(x) 最小的正零点小的正数.
解:因为f(0)>0,f(1)>0, f(2)>0, f(3)<0,
所以下次生产应在2个月后开始.
2. 点P从点O出发,按逆时针方向沿周长为l 的图形运动一周,O,P两点连线的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是 ( )
l
x
y
o
o
P
A
o
P
B
o
P
C
o
P
D
C
4. 设计四个杯子的形状,使得在向杯中匀速注水时,杯中水面的高度h随时间t变化的图象分别与下列图象相符合.
t
h
o
图(1)
t
h
o
图(2)
t
h
o
图(3)
t
h
o
图(4)
t
h
o
图(4)
3.列车从A地出发直达500km以外的B地,途中要经过离A地200km的C地。假设列车匀速前进,试画出列车与C地的距离s关于时间t的函数图象。
0
T
200
t
s
500
0.4T
解:设列车从A地到B地所用时间为T.
则当t=0时s=200;
当t=0.4T时s=0;
当t=T时s=500.
因为列车匀速行驶,所以距离s是时间t的一次函数,
B组 2:如图,△OAB是
边长为2的正三角形,记
△OAB位于直线x=t(t>0)
左侧的图形的面积为f(t).
试求函数f(t)的解析式,
并画出函数y=f(t)的图象.
0
A
B
x
y
x=t
{
解: y=f(t)=
