数学:1.2.2《函数及其表示(1)》课件(新人教A版必修1)
文档属性
| 名称 | 数学:1.2.2《函数及其表示(1)》课件(新人教A版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 743.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-17 19:45:07 | ||
图片预览





文档简介
(共25张PPT)
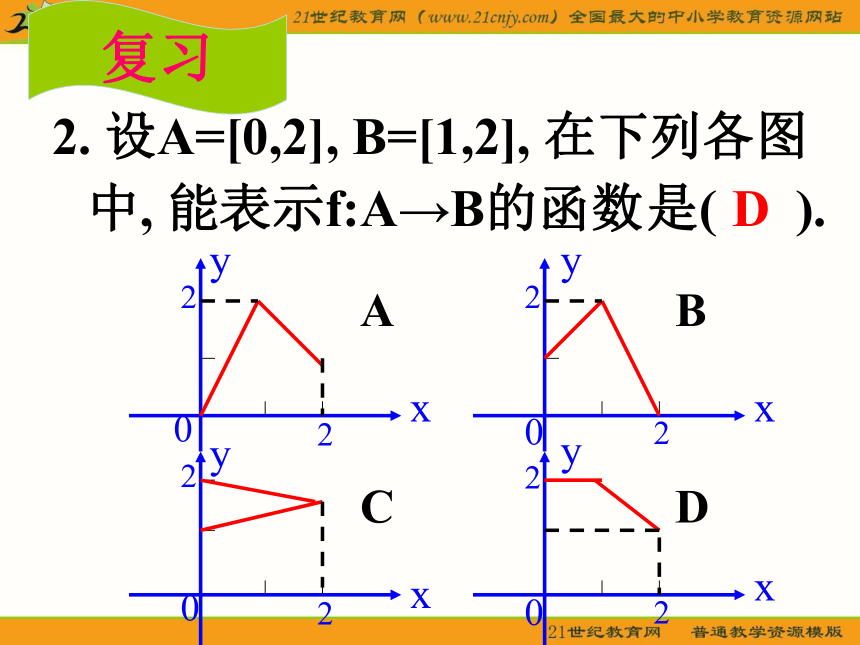
2. 设A=[0,2], B=[1,2], 在下列各图
中, 能表示f:A→B的函数
是( ).
x
x
x
x
y
y
y
y
0
0
0
0
2
2
2
2
2
2
2
2
A
B
C
D
D
复习
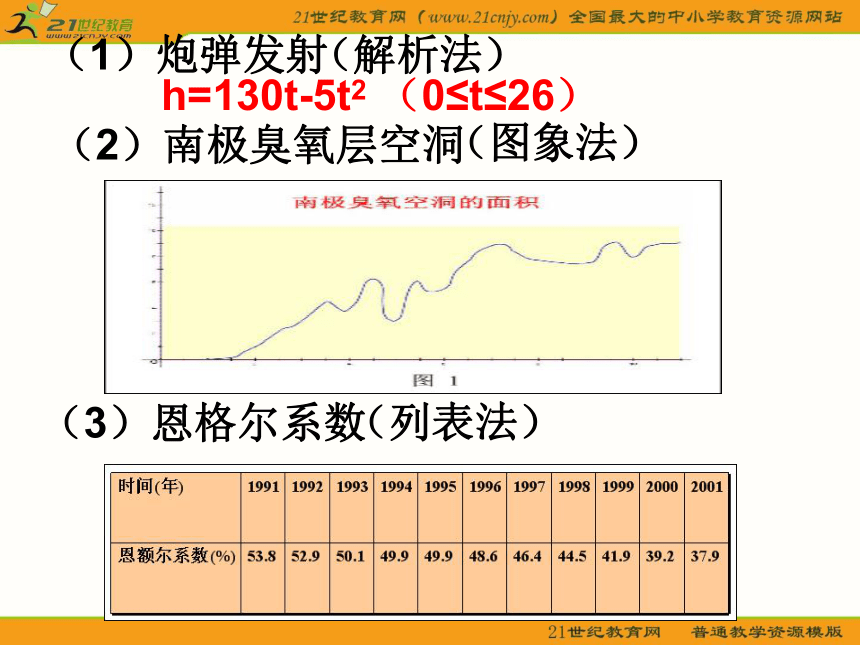
(1)炮弹发射
(解析法)
h=130t-5t2 (0≤t≤26)
(2)南极臭氧层空洞
(图象法)
(3)恩格尔系数
(列表法)
问题:在日常生活中,我们会遇到许多函数问题,如何选择适当的方式来表示问题中的函数关系呢?
知识探究(一)
例3 某种笔记本的单价是5元,买x (x∈{1,2,3,4,5})个笔记本需要y元.试用适当的方式表示函数y=f(x).
思考1:该函数用解析法怎样表示?
思考2:该函数用列表法怎样表示?
笔记本数 x 1 2 3 4 5
钱数 y 5 10 15 20 25
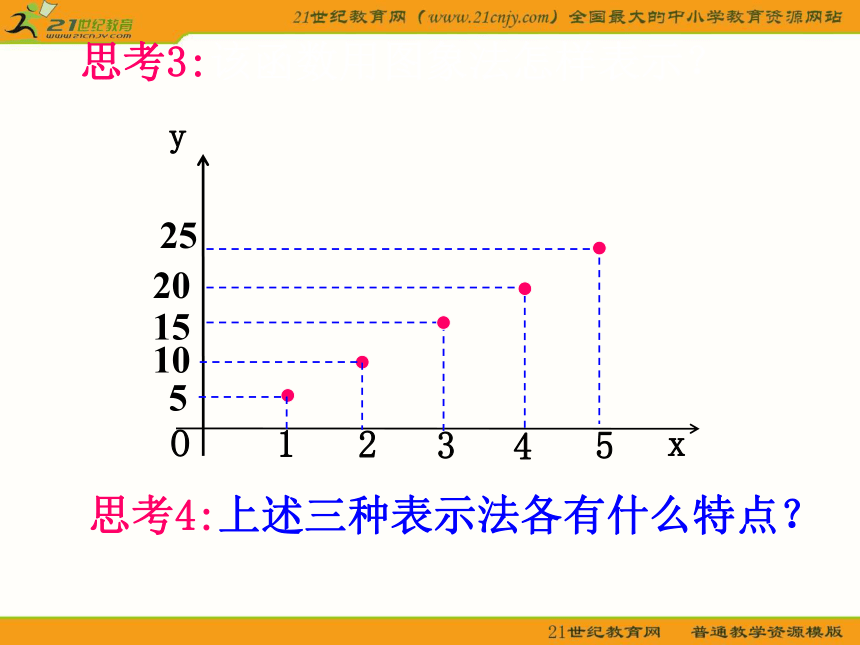
思考3:该函数用图象法怎样表示?
思考4:上述三种表示法各有什么特点?
y
O
x
5
4
3
2
1
5
10
20
25
15
优点 缺点
解析法 函数关系清楚,可以用代
入法求函数值,便于用解
析式研究函数的性质; 函数值随自变量变化
的规律不直观。
图象法 是可以直观形象地表示出函数的变化情况 在读取函数值时不够精确。
列表法 可以直接从表中读出函
数值 经常不可能把所有的
对应值列入数表中,而
只能达到实际上大致够
用的程度。
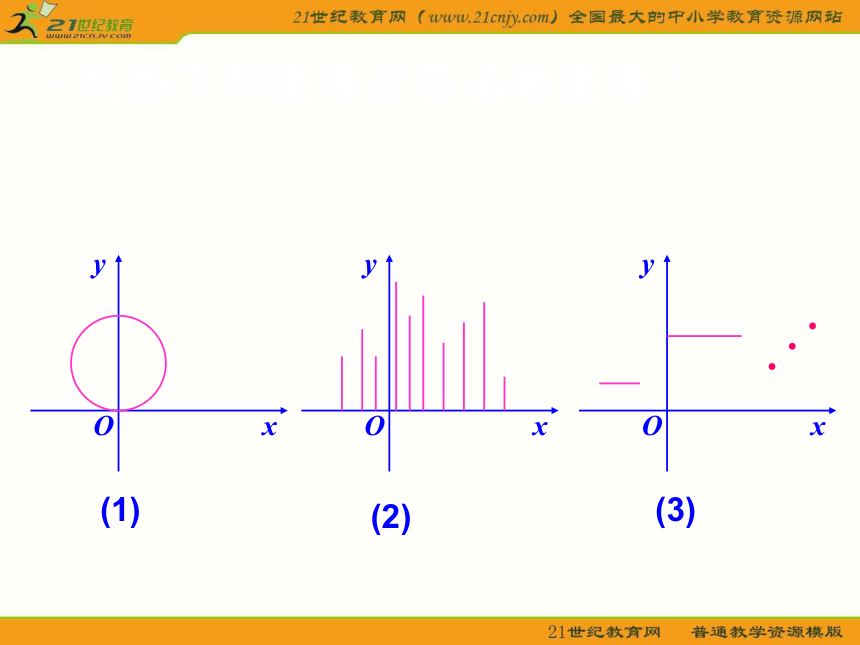
函数图像既可以是连续曲线,又可以是直线、折线、离散的点等等。那么判断一个图像是否函数图像的依据是什么?
判断下列图像是否函数图像?
O
x
y
(1)
O
x
y
(2)
O
x
y
(3)
知识探究(二)
例4 下表是某校高一(1)班三位同学在高一学年度六次数学测试的成绩及班级平均分表:
第1次 第2次 第3次 第4次 第5次 第6次
王 伟 98 87 91 92 88 95
张 城 90 76 88 75 86 80
赵 磊 68 65 73 72 75 82
班平分 88.2 78.3 85.4 80.3 75.7 82.6
思考1:上表反映了几个函数关系?这些函数的自变量是什么?定义域是什么?
思考2:上述4个函数能用解析法表示吗?能用图象法表示吗?
思考3:若分析、比较每位同学的成绩变化情况,用哪种表示法为宜?
王伟
平均分
赵磊
张城
100
O
x
y
5
4
3
2
1
6
90
80
70
60
思考4:试根据图象对这三位同学在高一学年度的数学学习情况做一个分析.
王伟
平均分
赵磊
张城
100
O
x
y
5
4
3
2
1
6
90
80
70
60
练习1:课本第23页第2题
例5 画出函数y=|x|的图象.
x
o
y
知识探究(三)
解:由绝对值的概念,有
所以,函数的图像如图所示。
练习:画出函数y=|x-2|的图像.
x
o
y
今后,在画出一些简单函数如一次函数、反比例函数、二次函数的图像时,我们可以不再列表,直接描点作出即可。
知识探究(三)
例6 某市某条公交线路的总里程是20公里,在这条线路上公交车“招手即停”,其票价如下:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按照5公里计算).
思考1:里程与票价之间的对应关系是否为函数?若是,函数的自变量是什么?定义域是什么?
思考2:该函数用解析法怎样表示?
解:设里程为x公里,票价为y元,则
思考3:该函数用列表法怎样表示?
里程x(公里) (0,5] (5,10] (10,15] (15,20]
票价y(元) 2 3 4 5
思考4:该函数用图象法怎样表示?
y
O
x
20
15
10
5
1
2
3
4
5
所谓“分段函数”,习惯上指在定义域的不同部
分,有不同的对应法则的函数,对它应有以下两点
基本认识:
(1)分段函数是一个函数,不要把它误认为是几
个函数;
(2)分段函数的定义域是各段定义域的并集,值
域是各段值域的并集。
课堂练习
1. 画出下列函数图象:
2. 已知函数f (x)=
2x+3, x<-1,
x2, -1≤x<1,
x-1, x≥1 .
求f{f[f(-2)]} ;
(2) 当f (x)=-7时,求x ;
解: (1) f{f[f(-2)]} = f{f[-1]}
= f(1)
= 0
(2)当x<-1 时, 2x+3 <1,与
f (x)=-7相符,由
2x+3 =-7得x=-5
易知其他二段均不符合f (x)=-7.
故x=-5
3. 已知函数f (x)=
x+2, (x≤-1)
x2, (-1<x<2)
2x, ( x≥2 )
若f(x)=3, 则x的值是( )
A. 1
B. 1或
C. 1, ,
D.
D
课堂小结
1. 本节主要学习了函数的三种表示方法:解析法、列表法和图象法的定义以及它们各自的优点.
2.分段函数的定义域为各段并集,值域为各段值域并集
作业:24页A组第5、6、7、8
2. 设A=[0,2], B=[1,2], 在下列各图
中, 能表示f:A→B的函数
是( ).
x
x
x
x
y
y
y
y
0
0
0
0
2
2
2
2
2
2
2
2
A
B
C
D
D
复习
(1)炮弹发射
(解析法)
h=130t-5t2 (0≤t≤26)
(2)南极臭氧层空洞
(图象法)
(3)恩格尔系数
(列表法)
问题:在日常生活中,我们会遇到许多函数问题,如何选择适当的方式来表示问题中的函数关系呢?
知识探究(一)
例3 某种笔记本的单价是5元,买x (x∈{1,2,3,4,5})个笔记本需要y元.试用适当的方式表示函数y=f(x).
思考1:该函数用解析法怎样表示?
思考2:该函数用列表法怎样表示?
笔记本数 x 1 2 3 4 5
钱数 y 5 10 15 20 25
思考3:该函数用图象法怎样表示?
思考4:上述三种表示法各有什么特点?
y
O
x
5
4
3
2
1
5
10
20
25
15
优点 缺点
解析法 函数关系清楚,可以用代
入法求函数值,便于用解
析式研究函数的性质; 函数值随自变量变化
的规律不直观。
图象法 是可以直观形象地表示出函数的变化情况 在读取函数值时不够精确。
列表法 可以直接从表中读出函
数值 经常不可能把所有的
对应值列入数表中,而
只能达到实际上大致够
用的程度。
函数图像既可以是连续曲线,又可以是直线、折线、离散的点等等。那么判断一个图像是否函数图像的依据是什么?
判断下列图像是否函数图像?
O
x
y
(1)
O
x
y
(2)
O
x
y
(3)
知识探究(二)
例4 下表是某校高一(1)班三位同学在高一学年度六次数学测试的成绩及班级平均分表:
第1次 第2次 第3次 第4次 第5次 第6次
王 伟 98 87 91 92 88 95
张 城 90 76 88 75 86 80
赵 磊 68 65 73 72 75 82
班平分 88.2 78.3 85.4 80.3 75.7 82.6
思考1:上表反映了几个函数关系?这些函数的自变量是什么?定义域是什么?
思考2:上述4个函数能用解析法表示吗?能用图象法表示吗?
思考3:若分析、比较每位同学的成绩变化情况,用哪种表示法为宜?
王伟
平均分
赵磊
张城
100
O
x
y
5
4
3
2
1
6
90
80
70
60
思考4:试根据图象对这三位同学在高一学年度的数学学习情况做一个分析.
王伟
平均分
赵磊
张城
100
O
x
y
5
4
3
2
1
6
90
80
70
60
练习1:课本第23页第2题
例5 画出函数y=|x|的图象.
x
o
y
知识探究(三)
解:由绝对值的概念,有
所以,函数的图像如图所示。
练习:画出函数y=|x-2|的图像.
x
o
y
今后,在画出一些简单函数如一次函数、反比例函数、二次函数的图像时,我们可以不再列表,直接描点作出即可。
知识探究(三)
例6 某市某条公交线路的总里程是20公里,在这条线路上公交车“招手即停”,其票价如下:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按照5公里计算).
思考1:里程与票价之间的对应关系是否为函数?若是,函数的自变量是什么?定义域是什么?
思考2:该函数用解析法怎样表示?
解:设里程为x公里,票价为y元,则
思考3:该函数用列表法怎样表示?
里程x(公里) (0,5] (5,10] (10,15] (15,20]
票价y(元) 2 3 4 5
思考4:该函数用图象法怎样表示?
y
O
x
20
15
10
5
1
2
3
4
5
所谓“分段函数”,习惯上指在定义域的不同部
分,有不同的对应法则的函数,对它应有以下两点
基本认识:
(1)分段函数是一个函数,不要把它误认为是几
个函数;
(2)分段函数的定义域是各段定义域的并集,值
域是各段值域的并集。
课堂练习
1. 画出下列函数图象:
2. 已知函数f (x)=
2x+3, x<-1,
x2, -1≤x<1,
x-1, x≥1 .
求f{f[f(-2)]} ;
(2) 当f (x)=-7时,求x ;
解: (1) f{f[f(-2)]} = f{f[-1]}
= f(1)
= 0
(2)当x<-1 时, 2x+3 <1,与
f (x)=-7相符,由
2x+3 =-7得x=-5
易知其他二段均不符合f (x)=-7.
故x=-5
3. 已知函数f (x)=
x+2, (x≤-1)
x2, (-1<x<2)
2x, ( x≥2 )
若f(x)=3, 则x的值是( )
A. 1
B. 1或
C. 1, ,
D.
D
课堂小结
1. 本节主要学习了函数的三种表示方法:解析法、列表法和图象法的定义以及它们各自的优点.
2.分段函数的定义域为各段并集,值域为各段值域并集
作业:24页A组第5、6、7、8
