冀教版数学六年级下册4.3圆柱的体积公式 课件(17张ppt)
文档属性
| 名称 | 冀教版数学六年级下册4.3圆柱的体积公式 课件(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 06:04:28 | ||
图片预览



文档简介
圆柱和圆锥
第3课时 圆柱的体积公式
1.经历认识圆柱体积、探索圆柱体积计算公式及简单应用的过程。
2.探索并掌握圆柱的体积公式,能用公式计算圆柱的体积。
3.在探索圆柱体积的过程中,体会转化和极限思想,获得探索数学公式的活动经验。
【重点】掌握圆柱的体积公式,并会计算圆柱的体积。
【难点】圆柱体积公式的探索和运用。
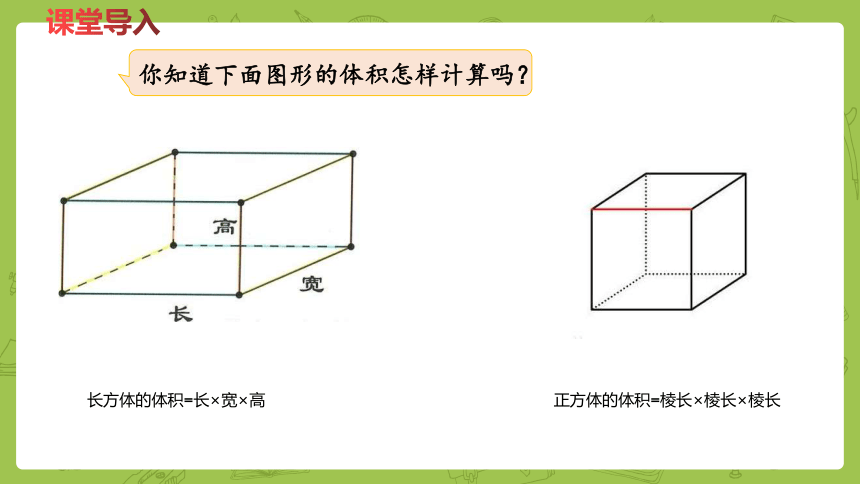
你知道下面图形的体积怎样计算吗?
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
亮亮和爷爷同一天过生日。
观察上面的情境,你想到了哪些问题?
两个蛋糕都是圆柱形的。
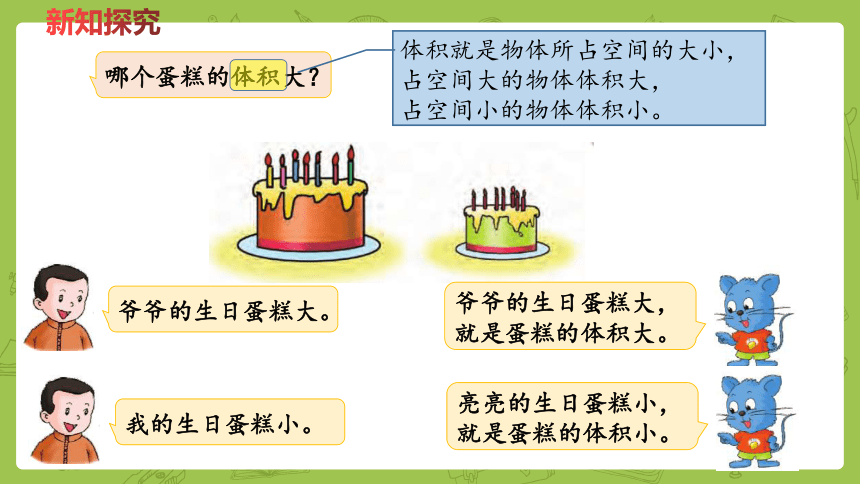
哪个蛋糕的体积大?
体积就是物体所占空间的大小,占空间大的物体体积大,
占空间小的物体体积小。
爷爷的生日蛋糕大。
爷爷的生日蛋糕大,就是蛋糕的体积大。
我的生日蛋糕小。
亮亮的生日蛋糕小,就是蛋糕的体积小。
下面是两个茶叶筒,怎样比较哪个茶叶筒的体积大呢?
哪个筒装茶叶多,哪个体积就大。
可以在茶叶筒中放入水,哪个筒装水多,哪个体积就大。
还可以称一称两个筒的重量,哪个筒重,哪个筒的体积就大。
要是能计算出体积就好了。
直观比较
第一个茶叶桶又细又高,第二个茶叶桶又矮又粗,不能准确比较出哪个茶叶桶的体积更大。
盛装物品比较
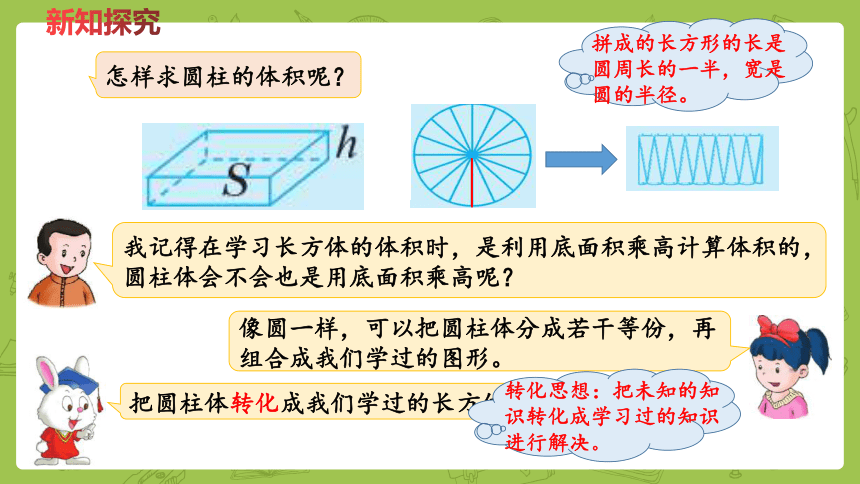
怎样求圆柱的体积呢?
我记得在学习长方体的体积时,是利用底面积乘高计算体积的,圆柱体会不会也是用底面积乘高呢?
像圆一样,可以把圆柱体分成若干等份,再组合成我们学过的图形。
把圆柱体转化成我们学过的长方体看一看。
转化思想:把未知的知识转化成学习过的知识进行解决。
拼成的长方形的长是圆周长的一半,宽是圆的半径。
探索圆柱的体积公式。
把圆柱等分为16等份
拼成一个近似的长方体
把圆柱等分为32等份
拼成一个近似的长方体
等分的份数越多,就越接近一个长方体。
拼成的近似长方体和圆柱有什么关系?
近似长方体的底面积就是圆柱的底面积。
近似长方体的高就是圆柱的高。
长方体的体积=底面积×高
底面积
×高
圆柱的体积=
课堂小结
圆柱的体积=底面积×高
如果用V表示圆柱的体积,S表示圆柱的底面积,h表示圆柱的高,那么圆柱的体积公式可以写成:
V = Sh
试一试:求右面罐头盒的体积。(单位:厘米)
已知底面直径和高都是10厘米
根据圆柱的体积=底面积×高
3.14×(10÷2)?×10
=3.14×25×10
=78.5×10
=785(立方厘米)
答:罐头盒的体积是785立方厘米。
1.计算下面圆柱的体积。
根据圆柱的体积=底面积×高
3.14×3?×6
=3.14×9×6
=28.26×6
=169.56(dm?)
答:体积是169.56 dm? 。
根据圆柱的体积=底面积×高
3.14×(4÷2)?×12
=3.14×4×12
=12.56×12
=150.72(cm?)
答:体积是150.72 cm? 。
2.一个易拉罐(如下图),它的体积是多少立方厘米?
根据圆柱的体积=底面积×高
3.14×(6÷2)?×12
=3.14×9×12
=28.26×12
=339.12( cm? )
答:它的体积是339.12 cm? 。
3.一根圆柱形的钢材,底面积是50平方厘米,高是1.5米。它的体积是多少立方厘米?
先统一单位:1.5米=150厘米
根据圆柱的体积=底面积×高
50×150=7500(立方厘米)
答:它的体积是7500立方厘米。
4.一个圆柱的体积是80cm?,底面积是16cm?。它的高是多少厘米?
根据圆柱的体积=底面积×高
80÷16=5(cm)
答:它的高是5cm。
得出圆柱的高=圆柱的体积÷底面积
圆柱的体积=底面积×高
V = Sh
圆柱的体积公式
完成相关练习
第3课时 圆柱的体积公式
1.经历认识圆柱体积、探索圆柱体积计算公式及简单应用的过程。
2.探索并掌握圆柱的体积公式,能用公式计算圆柱的体积。
3.在探索圆柱体积的过程中,体会转化和极限思想,获得探索数学公式的活动经验。
【重点】掌握圆柱的体积公式,并会计算圆柱的体积。
【难点】圆柱体积公式的探索和运用。
你知道下面图形的体积怎样计算吗?
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
亮亮和爷爷同一天过生日。
观察上面的情境,你想到了哪些问题?
两个蛋糕都是圆柱形的。
哪个蛋糕的体积大?
体积就是物体所占空间的大小,占空间大的物体体积大,
占空间小的物体体积小。
爷爷的生日蛋糕大。
爷爷的生日蛋糕大,就是蛋糕的体积大。
我的生日蛋糕小。
亮亮的生日蛋糕小,就是蛋糕的体积小。
下面是两个茶叶筒,怎样比较哪个茶叶筒的体积大呢?
哪个筒装茶叶多,哪个体积就大。
可以在茶叶筒中放入水,哪个筒装水多,哪个体积就大。
还可以称一称两个筒的重量,哪个筒重,哪个筒的体积就大。
要是能计算出体积就好了。
直观比较
第一个茶叶桶又细又高,第二个茶叶桶又矮又粗,不能准确比较出哪个茶叶桶的体积更大。
盛装物品比较
怎样求圆柱的体积呢?
我记得在学习长方体的体积时,是利用底面积乘高计算体积的,圆柱体会不会也是用底面积乘高呢?
像圆一样,可以把圆柱体分成若干等份,再组合成我们学过的图形。
把圆柱体转化成我们学过的长方体看一看。
转化思想:把未知的知识转化成学习过的知识进行解决。
拼成的长方形的长是圆周长的一半,宽是圆的半径。
探索圆柱的体积公式。
把圆柱等分为16等份
拼成一个近似的长方体
把圆柱等分为32等份
拼成一个近似的长方体
等分的份数越多,就越接近一个长方体。
拼成的近似长方体和圆柱有什么关系?
近似长方体的底面积就是圆柱的底面积。
近似长方体的高就是圆柱的高。
长方体的体积=底面积×高
底面积
×高
圆柱的体积=
课堂小结
圆柱的体积=底面积×高
如果用V表示圆柱的体积,S表示圆柱的底面积,h表示圆柱的高,那么圆柱的体积公式可以写成:
V = Sh
试一试:求右面罐头盒的体积。(单位:厘米)
已知底面直径和高都是10厘米
根据圆柱的体积=底面积×高
3.14×(10÷2)?×10
=3.14×25×10
=78.5×10
=785(立方厘米)
答:罐头盒的体积是785立方厘米。
1.计算下面圆柱的体积。
根据圆柱的体积=底面积×高
3.14×3?×6
=3.14×9×6
=28.26×6
=169.56(dm?)
答:体积是169.56 dm? 。
根据圆柱的体积=底面积×高
3.14×(4÷2)?×12
=3.14×4×12
=12.56×12
=150.72(cm?)
答:体积是150.72 cm? 。
2.一个易拉罐(如下图),它的体积是多少立方厘米?
根据圆柱的体积=底面积×高
3.14×(6÷2)?×12
=3.14×9×12
=28.26×12
=339.12( cm? )
答:它的体积是339.12 cm? 。
3.一根圆柱形的钢材,底面积是50平方厘米,高是1.5米。它的体积是多少立方厘米?
先统一单位:1.5米=150厘米
根据圆柱的体积=底面积×高
50×150=7500(立方厘米)
答:它的体积是7500立方厘米。
4.一个圆柱的体积是80cm?,底面积是16cm?。它的高是多少厘米?
根据圆柱的体积=底面积×高
80÷16=5(cm)
答:它的高是5cm。
得出圆柱的高=圆柱的体积÷底面积
圆柱的体积=底面积×高
V = Sh
圆柱的体积公式
完成相关练习
