冀教版数学六年级下册4.7圆锥和圆锥的体积公式 课件(17张ppt)
文档属性
| 名称 | 冀教版数学六年级下册4.7圆锥和圆锥的体积公式 课件(17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 06:15:31 | ||
图片预览



文档简介
圆柱和圆锥
第7课时 圆锥和圆锥的体积公式
1.通过观察、讨论、实验等活动,经历认识圆锥和探索圆锥体积计算公式的过程。
2.知道圆锥的各部分名称,探索并掌握圆锥的体积公式,会用公式计算圆锥的体积。
3.积极参加数学活动,了解圆锥和圆柱之间的联系,获得探索数学公式的活动经验。
【重点】知道圆锥各部分名称,掌握圆锥体积计算公式并会计算。
【难点】理解圆锥体积计算公式并会计算圆锥体积。
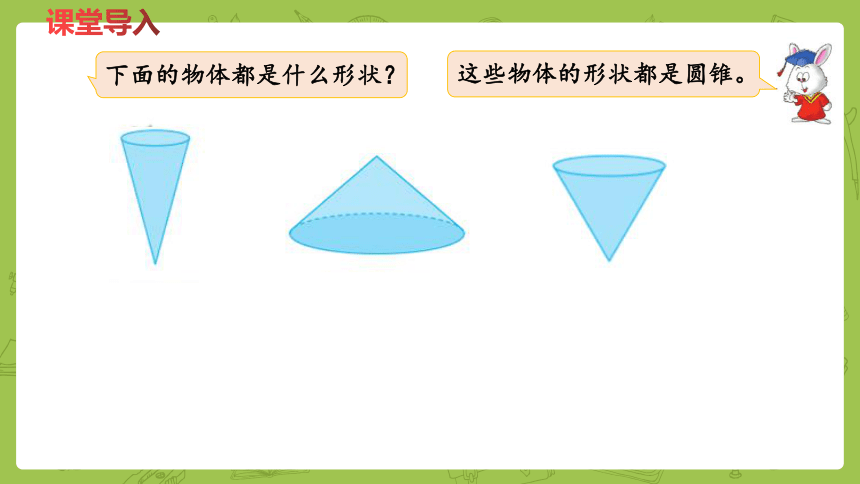
下面的物体都是什么形状?
这些物体的形状都是圆锥。
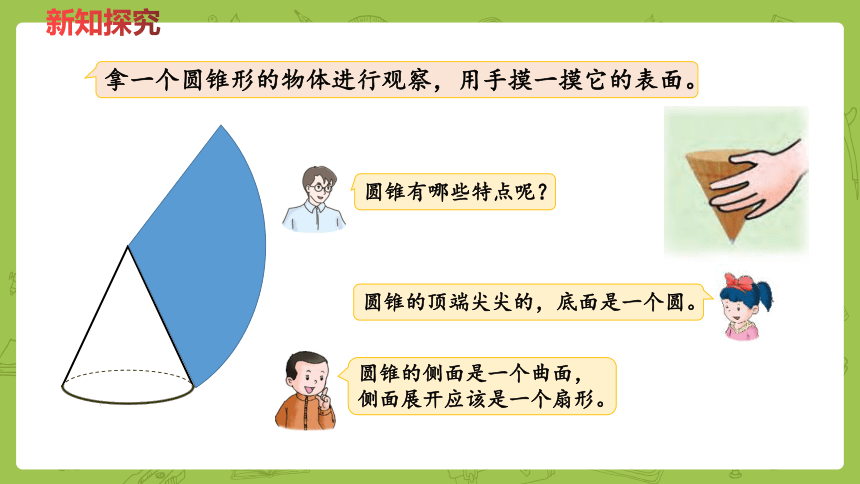
拿一个圆锥形的物体进行观察,用手摸一摸它的表面。
圆锥有哪些特点呢?
圆锥的顶端尖尖的,底面是一个圆。
圆锥的侧面是一个曲面,
侧面展开应该是一个扇形。
把圆锥表面剪开,会得到一个扇形和一个圆。
剪开
扇形
圆
圆锥只有两个面,
一个面是圆面,
一个面是曲面。
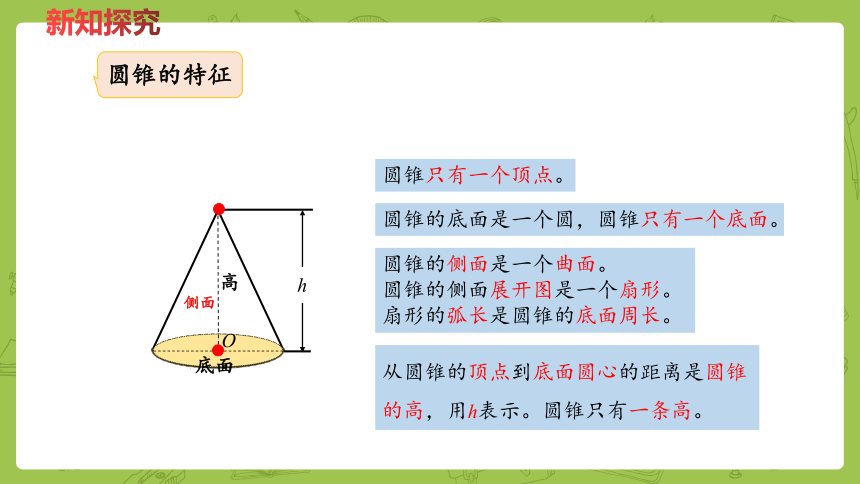
圆锥的特征
底面
h
.
O
侧面
圆锥的底面是一个圆,圆锥只有一个底面。
圆锥的侧面是一个曲面。
圆锥的侧面展开图是一个扇形。
扇形的弧长是圆锥的底面周长。
从圆锥的顶点到底面圆心的距离是圆锥的高,用h表示。圆锥只有一条高。
圆锥只有一个顶点。
高
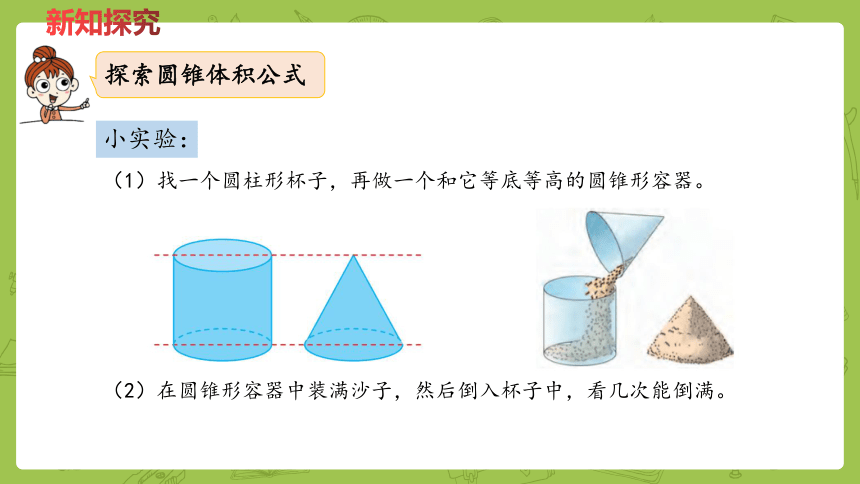
探索圆锥体积公式
小实验:
(1)找一个圆柱形杯子,再做一个和它等底等高的圆锥形容器。
(2)在圆锥形容器中装满沙子,然后倒入杯子中,看几次能倒满。
探索圆锥体积公式
(3)每倒入一次,测量一下杯子中沙子的高度,直到装满为止。边实验
边填写实验记录。
15厘米
8厘米
5厘米
10厘米
第三次
15厘米
圆锥中装满沙子,倒入与之等底等高的圆柱中,3次刚好倒满。
探索圆锥体积公式
实验用的圆柱和圆锥有什么关系?
实验用的圆柱和圆锥是等底等高的。
实验的结论说明什么?
说明圆锥的体积等于和它等底等高的圆柱体积的????????。
?
圆柱的体积 = 底面积 × 高
探索圆锥体积公式
如果用V表示圆锥的体积,S表示底面积,h表示高,
那么圆锥的体积公式可以写成:V=????????????h。
?
圆锥的体积 = 底面积 × 高 ×????????
?
圆锥的体积等于和它等底等高的圆柱体积的????????。
?
圆锥体积公式在不同情况下的应用。
已知圆锥的底面积和高,求圆锥的体积:
V = ???????? Sh
?
已知圆锥的底面半径和高,求圆锥的体积:
V = ????????πr?h
?
已知圆锥的底面直径和高,求圆锥的体积:
V = ????????π( ????2 )?h
?
已知圆锥的底面周长和高,求圆锥的体积:
V = ????????π( ????2???? )?h
?
1.指出下图中哪些是圆锥。
圆锥的顶端尖尖的,底面是一个圆。
不是圆锥
圆锥的侧面是一个曲面,
侧面展开应该是一个扇形。
是圆锥
不是圆锥
是圆锥
2.下面的圆柱和圆锥等底等高。已知圆柱的体积是45立方厘米,求圆锥的体积。
45÷3=15(立方厘米)
答:圆锥的体积是15立方厘米。
圆锥的体积等于和它等底等高的圆柱体积的????????。
?
3.计算右面圆锥的体积。
根据:圆锥的体积 = 底面积 × 高 ×13
?
答:这个圆锥的体积是25.12cm?。
3.14×(4÷2)?×6×13
=3.14×4×6×13
=12.56×6×13
=75.36×13
=25.12(cm?)
?
4.一个圆柱和一个圆锥等底等体积,已知圆柱的底面半径是6cm,它的体积是904.32cm?,圆柱和圆锥的高分别是多少厘米?
因为圆柱和圆锥体积相等,所以它们的体积都是904.32cm? 。
因为圆柱和圆锥底面积相等,所以它们的半径也相等,都是6cm 。
圆柱:904.32÷(3.14×6×6)=8(cm)
圆锥:904.32×3÷(3.14×6×6)=24(cm)
为什么乘3?
根据圆锥体积公式:
V = 13Sh。
?
得出:h=3V÷S ,所以要乘3。
圆柱的体积 = 底面积 × 高
圆锥的体积 = 底面积 × 高 ×13
?
圆锥的体积等于和它等底等高的圆柱体积的????????。
?
如果用V表示圆锥的体积,S表示底面积,h表示高,
那么圆锥的体积公式可以写成: V=13Sh
?
圆锥和圆锥的体积公式
练一练 第3、4题
第7课时 圆锥和圆锥的体积公式
1.通过观察、讨论、实验等活动,经历认识圆锥和探索圆锥体积计算公式的过程。
2.知道圆锥的各部分名称,探索并掌握圆锥的体积公式,会用公式计算圆锥的体积。
3.积极参加数学活动,了解圆锥和圆柱之间的联系,获得探索数学公式的活动经验。
【重点】知道圆锥各部分名称,掌握圆锥体积计算公式并会计算。
【难点】理解圆锥体积计算公式并会计算圆锥体积。
下面的物体都是什么形状?
这些物体的形状都是圆锥。
拿一个圆锥形的物体进行观察,用手摸一摸它的表面。
圆锥有哪些特点呢?
圆锥的顶端尖尖的,底面是一个圆。
圆锥的侧面是一个曲面,
侧面展开应该是一个扇形。
把圆锥表面剪开,会得到一个扇形和一个圆。
剪开
扇形
圆
圆锥只有两个面,
一个面是圆面,
一个面是曲面。
圆锥的特征
底面
h
.
O
侧面
圆锥的底面是一个圆,圆锥只有一个底面。
圆锥的侧面是一个曲面。
圆锥的侧面展开图是一个扇形。
扇形的弧长是圆锥的底面周长。
从圆锥的顶点到底面圆心的距离是圆锥的高,用h表示。圆锥只有一条高。
圆锥只有一个顶点。
高
探索圆锥体积公式
小实验:
(1)找一个圆柱形杯子,再做一个和它等底等高的圆锥形容器。
(2)在圆锥形容器中装满沙子,然后倒入杯子中,看几次能倒满。
探索圆锥体积公式
(3)每倒入一次,测量一下杯子中沙子的高度,直到装满为止。边实验
边填写实验记录。
15厘米
8厘米
5厘米
10厘米
第三次
15厘米
圆锥中装满沙子,倒入与之等底等高的圆柱中,3次刚好倒满。
探索圆锥体积公式
实验用的圆柱和圆锥有什么关系?
实验用的圆柱和圆锥是等底等高的。
实验的结论说明什么?
说明圆锥的体积等于和它等底等高的圆柱体积的????????。
?
圆柱的体积 = 底面积 × 高
探索圆锥体积公式
如果用V表示圆锥的体积,S表示底面积,h表示高,
那么圆锥的体积公式可以写成:V=????????????h。
?
圆锥的体积 = 底面积 × 高 ×????????
?
圆锥的体积等于和它等底等高的圆柱体积的????????。
?
圆锥体积公式在不同情况下的应用。
已知圆锥的底面积和高,求圆锥的体积:
V = ???????? Sh
?
已知圆锥的底面半径和高,求圆锥的体积:
V = ????????πr?h
?
已知圆锥的底面直径和高,求圆锥的体积:
V = ????????π( ????2 )?h
?
已知圆锥的底面周长和高,求圆锥的体积:
V = ????????π( ????2???? )?h
?
1.指出下图中哪些是圆锥。
圆锥的顶端尖尖的,底面是一个圆。
不是圆锥
圆锥的侧面是一个曲面,
侧面展开应该是一个扇形。
是圆锥
不是圆锥
是圆锥
2.下面的圆柱和圆锥等底等高。已知圆柱的体积是45立方厘米,求圆锥的体积。
45÷3=15(立方厘米)
答:圆锥的体积是15立方厘米。
圆锥的体积等于和它等底等高的圆柱体积的????????。
?
3.计算右面圆锥的体积。
根据:圆锥的体积 = 底面积 × 高 ×13
?
答:这个圆锥的体积是25.12cm?。
3.14×(4÷2)?×6×13
=3.14×4×6×13
=12.56×6×13
=75.36×13
=25.12(cm?)
?
4.一个圆柱和一个圆锥等底等体积,已知圆柱的底面半径是6cm,它的体积是904.32cm?,圆柱和圆锥的高分别是多少厘米?
因为圆柱和圆锥体积相等,所以它们的体积都是904.32cm? 。
因为圆柱和圆锥底面积相等,所以它们的半径也相等,都是6cm 。
圆柱:904.32÷(3.14×6×6)=8(cm)
圆锥:904.32×3÷(3.14×6×6)=24(cm)
为什么乘3?
根据圆锥体积公式:
V = 13Sh。
?
得出:h=3V÷S ,所以要乘3。
圆柱的体积 = 底面积 × 高
圆锥的体积 = 底面积 × 高 ×13
?
圆锥的体积等于和它等底等高的圆柱体积的????????。
?
如果用V表示圆锥的体积,S表示底面积,h表示高,
那么圆锥的体积公式可以写成: V=13Sh
?
圆锥和圆锥的体积公式
练一练 第3、4题
