冀教版 六年级数学下册3.1成正比例的量课件(16张PPT)
文档属性
| 名称 | 冀教版 六年级数学下册3.1成正比例的量课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 00:00:00 | ||
图片预览



文档简介
正比例 反比例
第1课时 成正比例的量
1.结合具体事例,经历认识和判断成正比例的量的过程。
2.知道正比例的意义,能判断两种量是否成正比例,能找出生活中成正比例的实例,并进行交流。
3.对现实生活中成正比例的事物有好奇心,在判断成正比例的量的过程中,能进行有条理的思考。
【重点】判断两种相关联的量是否成正比例。
【难点】理解正比例的意义,并判断两种量是否成正比例。
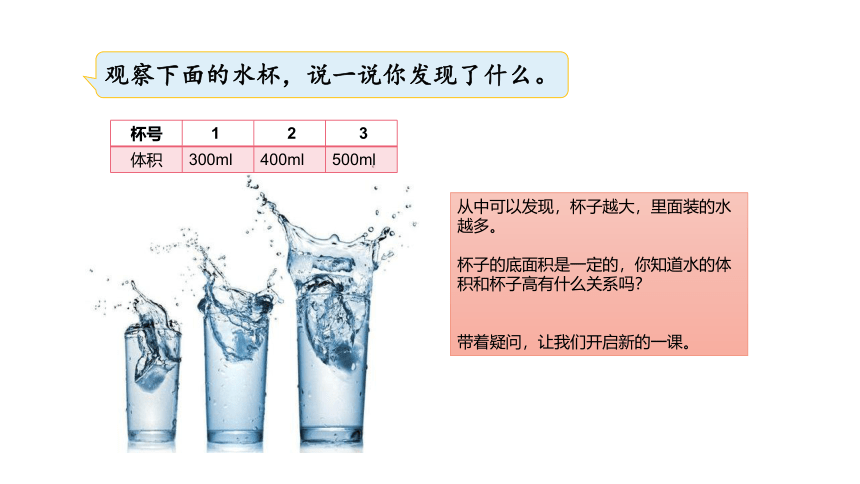
观察下面的水杯,说一说你发现了什么。
从中可以发现,杯子越大,里面装的水越多。
杯子的底面积是一定的,你知道水的体积和杯子高有什么关系吗?
带着疑问,让我们开启新的一课。
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3} 杯号
1
2
3
体积
300ml
400ml
500ml
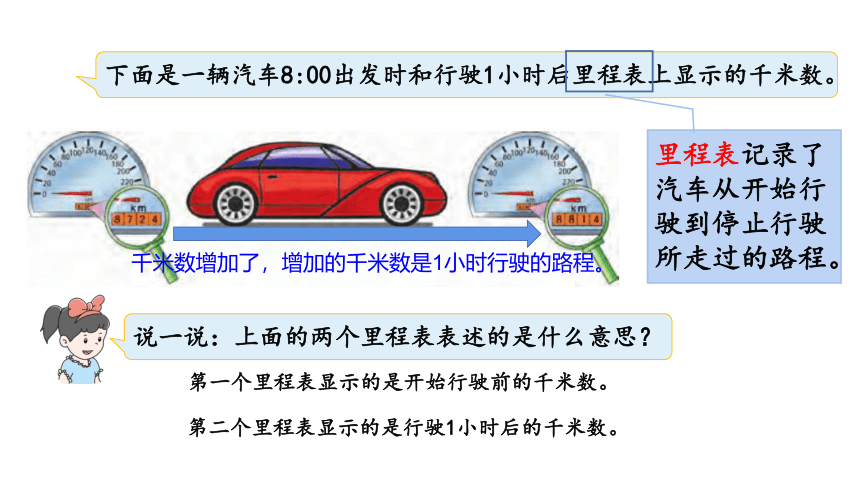
下面是一辆汽车8:00出发时和行驶1小时后里程表上显示的千米数。
说一说:上面的两个里程表表述的是什么意思?
里程表记录了汽车从开始行驶到停止行驶所走过的路程。
第一个里程表显示的是开始行驶前的千米数。
第二个里程表显示的是行驶1小时后的千米数。
千米数增加了,增加的千米数是1小时行驶的路程。
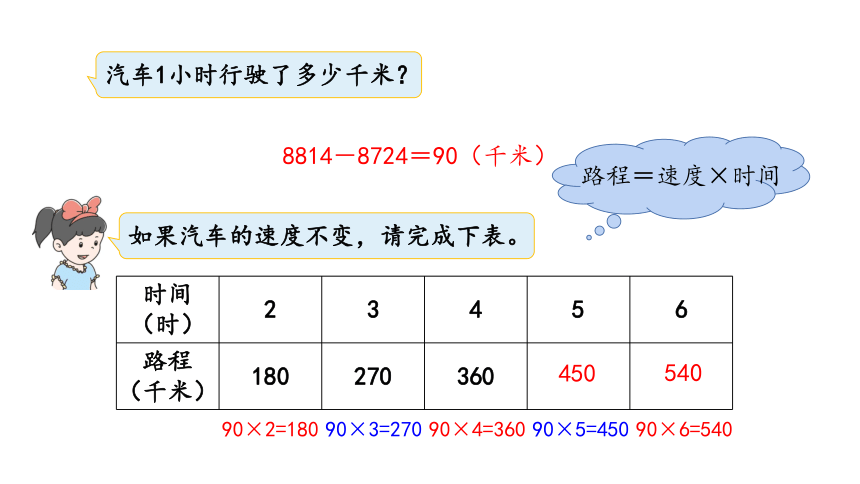
汽车1小时行驶了多少千米?
8814-8724=90(千米)
如果汽车的速度不变,请完成下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间(时)
2
3
4
5
6
路程(千米)
180
270
360
90×5=450
450
90×6=540
540
路程=速度×时间
90×2=180
90×3=270
90×4=360
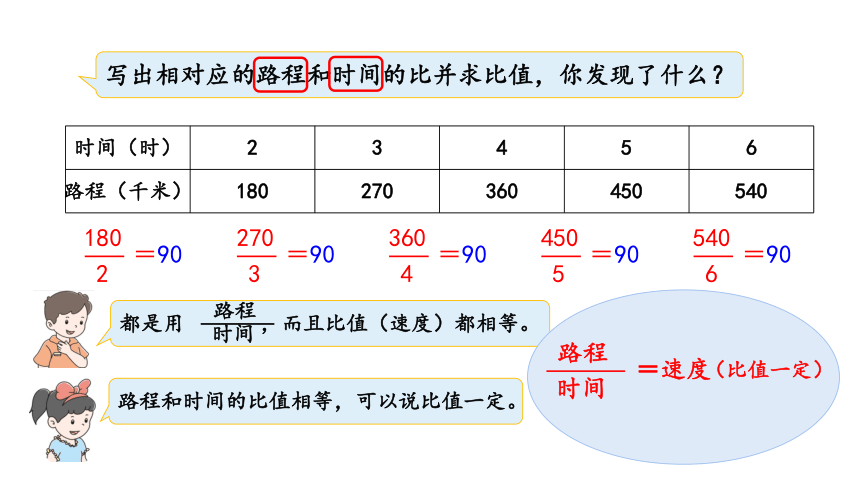
写出相对应的路程和时间的比并求比值,你发现了什么?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间(时)
2
3
4
5
6
路程(千米)
180
270
360
450
540
180
2
=90
270
3
=90
360
4
=90
450
5
=90
540
6
=90
都是用 ,而且比值(速度)都相等。
路程
时间
路程和时间的比值相等,可以说比值一定。
(比值一定)
路程
时间
=速度
在速度一定的情况下,路程和时间有什么关系?
速度一定,时间越长,行驶的路程也就越长。
速度每小时90千米,行驶6小时的路程比行驶5小时的路程长。
90×6=540(千米) 90×5=450(千米) 540>450
速度一定,路程越远,需要的时间越长。
速度每小时90千米,行驶540千米比行驶450千米需要的时间长。
540÷90=6(时) 450÷90=5(时) 6>5
速度×时间=路程
路程÷速度=时间
路程÷时间=速度
在上面的问题中,路程和时间是两种相关联的量,路程随着时间的变化而变化,而且,路程和时间的比值一定(速度一定)。我们说路程和时间这两种量成正比例。
两种相关联的量是指一种量变化,另一种量随之发生变化。
两种量有可能是和差关系,也有可能是积商关系。
例如: a+b=4
有可能是:1+3=4
2+2=4
例如: m×n=6
有可能是:1×6=6
2×3=6
总之,一种量随着另一种量的变化而变化。
可以简单说成:当两种相关联的量比值一定时,这两种量成正比例。
自动笔的单价为1.6元,请完成下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}数量(支)
2
3
4
5
6
7
8
总价(元)
3.2
4.8
6.4
8
9.6
11.2
12.8
总价=单价×数量
1.6×2
1.6×3
1.6×4
1.6×5
1.6×6
1.6×7
1.6×8
从上表中你发现了什么规律?
买自动笔的数量越多,花的钱数就越多……
单价一定,也就是花的钱数和买自动笔数量的比值一定。
总价
数量
=单价(一定)
还可以简单说成:因为 =单价(一定),所以买自动
笔的总价和数量成正比例。
总价
数量
花的钱数和买自动笔的数量这两种量成正比例吗?为什么?
1.花的钱数和买自动笔的数量是两种相关联的量。单价一定,总价随着买自动笔数量的变化而变化。
2.像上面这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量叫做成正比例的量。它们的关系叫做正比例关系。
如何判断两种量是否成正比例?
1. 判断两种量是不是两种相关联的量。
2.判断这两种量中相对应的两个数的比值是否一定,比值一定,则成正比例,比值不一定,则不成正比例。
1.判断下面各题中的两种量是否成正比例,并说明理由。
(1)飞机飞行的速度不变,飞行的路程和时间。
(2)每千克苹果的价钱一定,付出的钱数和购买苹果的数量。
(3)每月收入一定,每月支出的钱数和剩下的钱数。
成正比例,因为 ,所以飞行的路程和时间成正比例。
路程
时间
=速度(一定)
成正比例,因为 ,
所以付出的钱数和购买苹果的数量成正比例。
付出的钱数
买苹果的数量
=每千克苹果的价钱(一定)
总价=单价×数量
不成正比例,虽然支出的钱数和剩余的钱数也是两种相关联的量,但是这两种量仅仅是一种和差关系,不存在比值一定一说。
2.判断下面各题中的两种量是否成正比例,是正比例关系的在括号里打“√”。
(1)每天节约的钱数一定,节约的总钱数和天数。 ( )
(2)平行四边形的高一定,底和面积。 ( )
(3)一个人的身高和年龄。 ( )
节约的总钱数
天数
=每天节约的钱数(一定)
√
平行四边形面积
平行四边形的底
=平行四边形的高(一定)
√
×
3.一个化肥厂的生产情况如下表,根据表中数据回答问题。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间(天)
1
2
3
4
5
6
7
生产量(吨)
80
160
240
320
400
480
560
(1)表中有哪两种相关联的量?
时间和生产量是两种相关联的量。
(2)表中相关联的两种量成正比例吗?为什么?
80
1
=80
160
2
=80
时间和生产量成正比例,因为
生产量
时间
=生产效率(一定)。
240
3
=80
生产量
时间
=生产效率(一定)
在判断两种量是否成正比例时,先判断两种量是不是两种相关联的量;再判断这两种量中相对应的两个数的比值是否一定,比值一定,则成正比例,比值不一定,则不成正比例。
再见!
第1课时 成正比例的量
1.结合具体事例,经历认识和判断成正比例的量的过程。
2.知道正比例的意义,能判断两种量是否成正比例,能找出生活中成正比例的实例,并进行交流。
3.对现实生活中成正比例的事物有好奇心,在判断成正比例的量的过程中,能进行有条理的思考。
【重点】判断两种相关联的量是否成正比例。
【难点】理解正比例的意义,并判断两种量是否成正比例。
观察下面的水杯,说一说你发现了什么。
从中可以发现,杯子越大,里面装的水越多。
杯子的底面积是一定的,你知道水的体积和杯子高有什么关系吗?
带着疑问,让我们开启新的一课。
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3} 杯号
1
2
3
体积
300ml
400ml
500ml
下面是一辆汽车8:00出发时和行驶1小时后里程表上显示的千米数。
说一说:上面的两个里程表表述的是什么意思?
里程表记录了汽车从开始行驶到停止行驶所走过的路程。
第一个里程表显示的是开始行驶前的千米数。
第二个里程表显示的是行驶1小时后的千米数。
千米数增加了,增加的千米数是1小时行驶的路程。
汽车1小时行驶了多少千米?
8814-8724=90(千米)
如果汽车的速度不变,请完成下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间(时)
2
3
4
5
6
路程(千米)
180
270
360
90×5=450
450
90×6=540
540
路程=速度×时间
90×2=180
90×3=270
90×4=360
写出相对应的路程和时间的比并求比值,你发现了什么?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间(时)
2
3
4
5
6
路程(千米)
180
270
360
450
540
180
2
=90
270
3
=90
360
4
=90
450
5
=90
540
6
=90
都是用 ,而且比值(速度)都相等。
路程
时间
路程和时间的比值相等,可以说比值一定。
(比值一定)
路程
时间
=速度
在速度一定的情况下,路程和时间有什么关系?
速度一定,时间越长,行驶的路程也就越长。
速度每小时90千米,行驶6小时的路程比行驶5小时的路程长。
90×6=540(千米) 90×5=450(千米) 540>450
速度一定,路程越远,需要的时间越长。
速度每小时90千米,行驶540千米比行驶450千米需要的时间长。
540÷90=6(时) 450÷90=5(时) 6>5
速度×时间=路程
路程÷速度=时间
路程÷时间=速度
在上面的问题中,路程和时间是两种相关联的量,路程随着时间的变化而变化,而且,路程和时间的比值一定(速度一定)。我们说路程和时间这两种量成正比例。
两种相关联的量是指一种量变化,另一种量随之发生变化。
两种量有可能是和差关系,也有可能是积商关系。
例如: a+b=4
有可能是:1+3=4
2+2=4
例如: m×n=6
有可能是:1×6=6
2×3=6
总之,一种量随着另一种量的变化而变化。
可以简单说成:当两种相关联的量比值一定时,这两种量成正比例。
自动笔的单价为1.6元,请完成下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}数量(支)
2
3
4
5
6
7
8
总价(元)
3.2
4.8
6.4
8
9.6
11.2
12.8
总价=单价×数量
1.6×2
1.6×3
1.6×4
1.6×5
1.6×6
1.6×7
1.6×8
从上表中你发现了什么规律?
买自动笔的数量越多,花的钱数就越多……
单价一定,也就是花的钱数和买自动笔数量的比值一定。
总价
数量
=单价(一定)
还可以简单说成:因为 =单价(一定),所以买自动
笔的总价和数量成正比例。
总价
数量
花的钱数和买自动笔的数量这两种量成正比例吗?为什么?
1.花的钱数和买自动笔的数量是两种相关联的量。单价一定,总价随着买自动笔数量的变化而变化。
2.像上面这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量叫做成正比例的量。它们的关系叫做正比例关系。
如何判断两种量是否成正比例?
1. 判断两种量是不是两种相关联的量。
2.判断这两种量中相对应的两个数的比值是否一定,比值一定,则成正比例,比值不一定,则不成正比例。
1.判断下面各题中的两种量是否成正比例,并说明理由。
(1)飞机飞行的速度不变,飞行的路程和时间。
(2)每千克苹果的价钱一定,付出的钱数和购买苹果的数量。
(3)每月收入一定,每月支出的钱数和剩下的钱数。
成正比例,因为 ,所以飞行的路程和时间成正比例。
路程
时间
=速度(一定)
成正比例,因为 ,
所以付出的钱数和购买苹果的数量成正比例。
付出的钱数
买苹果的数量
=每千克苹果的价钱(一定)
总价=单价×数量
不成正比例,虽然支出的钱数和剩余的钱数也是两种相关联的量,但是这两种量仅仅是一种和差关系,不存在比值一定一说。
2.判断下面各题中的两种量是否成正比例,是正比例关系的在括号里打“√”。
(1)每天节约的钱数一定,节约的总钱数和天数。 ( )
(2)平行四边形的高一定,底和面积。 ( )
(3)一个人的身高和年龄。 ( )
节约的总钱数
天数
=每天节约的钱数(一定)
√
平行四边形面积
平行四边形的底
=平行四边形的高(一定)
√
×
3.一个化肥厂的生产情况如下表,根据表中数据回答问题。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间(天)
1
2
3
4
5
6
7
生产量(吨)
80
160
240
320
400
480
560
(1)表中有哪两种相关联的量?
时间和生产量是两种相关联的量。
(2)表中相关联的两种量成正比例吗?为什么?
80
1
=80
160
2
=80
时间和生产量成正比例,因为
生产量
时间
=生产效率(一定)。
240
3
=80
生产量
时间
=生产效率(一定)
在判断两种量是否成正比例时,先判断两种量是不是两种相关联的量;再判断这两种量中相对应的两个数的比值是否一定,比值一定,则成正比例,比值不一定,则不成正比例。
再见!
