冀教版 六年级数学下册3.2画图表示成正比例的量课件(17张PPT)
文档属性
| 名称 | 冀教版 六年级数学下册3.2画图表示成正比例的量课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 14:29:49 | ||
图片预览





文档简介
正比例 反比例
第2课时 画图表示成正比例的量
1.结合具体事例,经历在方格纸上表示成正比例关系的量,并回答问题的过程。
2.能在方格纸上画图表示成正比例的量,会根据其中一个量的值估计另一个量的值。
3.体会借助图形解决问题的价值,感受数形结合思想。
【重点】在方格纸上画图表示成正比例的量,根据已知量估计未知量。
【难点】理解成正比例的两种量的变化规律与直线的关系。
张老师计划装饰一下教室,会用到什么物品呢?
气球
彩带
每米4元
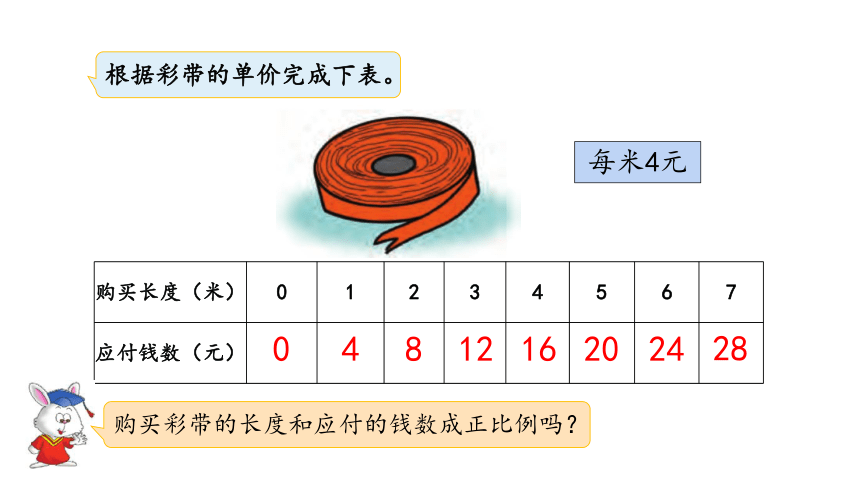
根据彩带的单价完成下表。
每米4元
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}购买长度(米)
0
1
2
3
4
5
6
7
应付钱数(元)
0
4
8
12
16
20
24
28
购买彩带的长度和应付的钱数成正比例吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}购买长度(米)
0
1
2
3
4
5
6
7
应付钱数(元)
0
4
8
12
16
20
24
28
购买彩带的长度和应付的钱数成正比例吗?
购买彩带的长度和应付的钱数成正比例,因为:
应付钱数
购买长度
=彩带单价(一定)
应付钱数和购买长度的比值都是4,正好是彩带的单价。
在计算比值时,不考虑0:0,因为0:0没有意义。
购买彩带的长度和应付的钱数
是两种相关联的量。
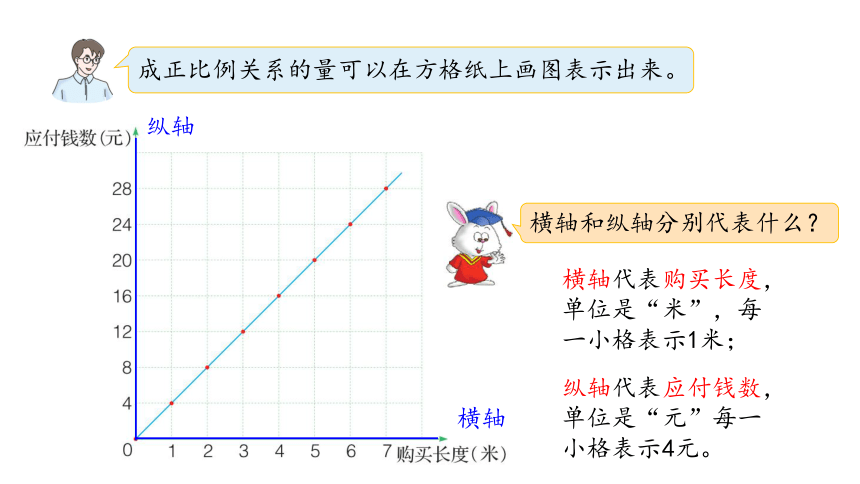
成正比例关系的量可以在方格纸上画图表示出来。
横轴
纵轴
横轴和纵轴分别代表什么?
横轴代表购买长度,单位是“米”,每一小格表示1米;
纵轴代表应付钱数,单位是“元”每一小格表示4元。
图中的红点表示什么,是怎样画出来的?
当购买长度是1米时,应付钱数4元。
当购买长度是2米时,应付钱数8元。
当购买长度是3米时,应付钱数12元。
当购买长度是4米时,应付钱数16元。
当购买长度是5米时,应付钱数20元。
当购买长度是6米时,应付钱数24元。
当购买长度是7米时,应付钱数28元。
当购买长度是0米时,应付钱数0元。
(0,0)
(1,4)
(2,8)
(3,12)
(4,16)
(5,20)
(6,24)
(7,28)
可以把红点用数对表示出来,“列”对应购买长度, “排”对应应付钱数。
应付钱数
图中的红点表示什么,是怎样画出来的?
(0,0)
(1,4)
(2,8)
(3,12)
(4,16)
(5,20)
(6,24)
(7,28)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}购买长度(米)
0
1
2
3
4
5
6
7
应付钱数(元)
0
4
8
12
16
20
24
28
把表格中的对应数据也按照“列”对应购买长度,“排”对应应付钱数写成数对,分别是(0,0)(1,4)(2,8)(3,12)(4,16)(5,20)(6,24)(7,28)然后依次连线画出的图形。
表示正比例关系的图像有什么特点?
是一条射线。
起点是横轴和纵轴的交点。
购买长度和应付钱数两种量的所有对应点都在这条射线上。
当购买长度是2米时,对应应付钱数8元。
当购买长度是5米时,对应应付钱数20元。
不计算,看图估计一下:买1.5米彩带要花多少元?买5.5米呢?
1.5
6
通过估计,购买1.5米彩带需要6元。购买5.5米彩带需要22元。
5.5
22
①先在横轴上找到表示1.5米的点,并从这点向上做出横轴的垂线,得到垂线与已知点的交点。
②从交点起做纵轴的垂线,纵轴上垂足对应6元,即买1.5米彩带需要6元。
③同样的方法可以估计买5.5米彩带需要22元。
你还能提出哪些数学问题?
10元能买几米彩带?
10
一辆汽车平均每小时行驶80千米。
(1)照上面的速度计算,完成下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间(时)
0
1
2
3
4
5
6
7
路程
(千米)
0
80
160
240
320
400
480
560
80×1=80(千米)
80×2=160(千米)
80×3=240(千米)
80×4=320(千米)
80×5=400(千米)
80×6=480(千米)
80×7=560(千米)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间(时)
0
1
2
3
4
5
6
7
路程
(千米)
0
80
160
240
320
400
480
560
(2)把表中的数据在右面的方格纸上画图表示出来。
(0,0)
(1,80)
(2,160)
(3,240)
(4,320)
(5,400)
(6,480)
(7,560)
先把对应的数对写出来。
再从方格图中找出对应的数对。
最后连线。
2.小玲用计算机打字的个数和所用的时间如下表。
(1)小玲打字的个数和所用的时间成正比例吗?为什么?
时间/分
数量/个
2
4
6
8
10
12
14
100
200
300
400
500
600
700
成正比例。
因为:打字个数和所用时间是两种相关联的量。
打字个数
所用时间
=每分钟打字的个数(一定)
2.小玲用计算机打字的个数和所用的时间如下表。
(2)根据表中的数据,在下图中描出打字数量和时间所对应的点,再把它们按顺序连接起来。
时间/分
数量/个
2
4
6
8
10
12
14
100
200
300
400
500
600
700
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 时间/分
数量/个
800
700
600
500
400
300
200
100
2.小玲用计算机打字的个数和所用的时间如下表。
(3)看图估计小玲5分钟打了多少个字?打750个字要多少分钟?
时间/分
数量/个
2
4
6
8
10
12
14
100
200
300
400
500
600
700
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 时间/分
数量/个
800
700
600
500
400
300
200
100
250
答:小玲5分钟大约打了250个字。打750个字大约要15分钟。
画图方法:把表格中的对应数据写成数对,然后在方格纸上找出这些数对,依次连线画出图像。
表示正比例关系的图像特点:
1、图像是从横轴和纵轴的交点画出的一条射线。
2、横轴和纵轴表示的两种量的所有对应点都在这
条射线上。
画图表示成正比例的量
练一练 第2、3题
第2课时 画图表示成正比例的量
1.结合具体事例,经历在方格纸上表示成正比例关系的量,并回答问题的过程。
2.能在方格纸上画图表示成正比例的量,会根据其中一个量的值估计另一个量的值。
3.体会借助图形解决问题的价值,感受数形结合思想。
【重点】在方格纸上画图表示成正比例的量,根据已知量估计未知量。
【难点】理解成正比例的两种量的变化规律与直线的关系。
张老师计划装饰一下教室,会用到什么物品呢?
气球
彩带
每米4元
根据彩带的单价完成下表。
每米4元
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}购买长度(米)
0
1
2
3
4
5
6
7
应付钱数(元)
0
4
8
12
16
20
24
28
购买彩带的长度和应付的钱数成正比例吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}购买长度(米)
0
1
2
3
4
5
6
7
应付钱数(元)
0
4
8
12
16
20
24
28
购买彩带的长度和应付的钱数成正比例吗?
购买彩带的长度和应付的钱数成正比例,因为:
应付钱数
购买长度
=彩带单价(一定)
应付钱数和购买长度的比值都是4,正好是彩带的单价。
在计算比值时,不考虑0:0,因为0:0没有意义。
购买彩带的长度和应付的钱数
是两种相关联的量。
成正比例关系的量可以在方格纸上画图表示出来。
横轴
纵轴
横轴和纵轴分别代表什么?
横轴代表购买长度,单位是“米”,每一小格表示1米;
纵轴代表应付钱数,单位是“元”每一小格表示4元。
图中的红点表示什么,是怎样画出来的?
当购买长度是1米时,应付钱数4元。
当购买长度是2米时,应付钱数8元。
当购买长度是3米时,应付钱数12元。
当购买长度是4米时,应付钱数16元。
当购买长度是5米时,应付钱数20元。
当购买长度是6米时,应付钱数24元。
当购买长度是7米时,应付钱数28元。
当购买长度是0米时,应付钱数0元。
(0,0)
(1,4)
(2,8)
(3,12)
(4,16)
(5,20)
(6,24)
(7,28)
可以把红点用数对表示出来,“列”对应购买长度, “排”对应应付钱数。
应付钱数
图中的红点表示什么,是怎样画出来的?
(0,0)
(1,4)
(2,8)
(3,12)
(4,16)
(5,20)
(6,24)
(7,28)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}购买长度(米)
0
1
2
3
4
5
6
7
应付钱数(元)
0
4
8
12
16
20
24
28
把表格中的对应数据也按照“列”对应购买长度,“排”对应应付钱数写成数对,分别是(0,0)(1,4)(2,8)(3,12)(4,16)(5,20)(6,24)(7,28)然后依次连线画出的图形。
表示正比例关系的图像有什么特点?
是一条射线。
起点是横轴和纵轴的交点。
购买长度和应付钱数两种量的所有对应点都在这条射线上。
当购买长度是2米时,对应应付钱数8元。
当购买长度是5米时,对应应付钱数20元。
不计算,看图估计一下:买1.5米彩带要花多少元?买5.5米呢?
1.5
6
通过估计,购买1.5米彩带需要6元。购买5.5米彩带需要22元。
5.5
22
①先在横轴上找到表示1.5米的点,并从这点向上做出横轴的垂线,得到垂线与已知点的交点。
②从交点起做纵轴的垂线,纵轴上垂足对应6元,即买1.5米彩带需要6元。
③同样的方法可以估计买5.5米彩带需要22元。
你还能提出哪些数学问题?
10元能买几米彩带?
10
一辆汽车平均每小时行驶80千米。
(1)照上面的速度计算,完成下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间(时)
0
1
2
3
4
5
6
7
路程
(千米)
0
80
160
240
320
400
480
560
80×1=80(千米)
80×2=160(千米)
80×3=240(千米)
80×4=320(千米)
80×5=400(千米)
80×6=480(千米)
80×7=560(千米)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间(时)
0
1
2
3
4
5
6
7
路程
(千米)
0
80
160
240
320
400
480
560
(2)把表中的数据在右面的方格纸上画图表示出来。
(0,0)
(1,80)
(2,160)
(3,240)
(4,320)
(5,400)
(6,480)
(7,560)
先把对应的数对写出来。
再从方格图中找出对应的数对。
最后连线。
2.小玲用计算机打字的个数和所用的时间如下表。
(1)小玲打字的个数和所用的时间成正比例吗?为什么?
时间/分
数量/个
2
4
6
8
10
12
14
100
200
300
400
500
600
700
成正比例。
因为:打字个数和所用时间是两种相关联的量。
打字个数
所用时间
=每分钟打字的个数(一定)
2.小玲用计算机打字的个数和所用的时间如下表。
(2)根据表中的数据,在下图中描出打字数量和时间所对应的点,再把它们按顺序连接起来。
时间/分
数量/个
2
4
6
8
10
12
14
100
200
300
400
500
600
700
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 时间/分
数量/个
800
700
600
500
400
300
200
100
2.小玲用计算机打字的个数和所用的时间如下表。
(3)看图估计小玲5分钟打了多少个字?打750个字要多少分钟?
时间/分
数量/个
2
4
6
8
10
12
14
100
200
300
400
500
600
700
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 时间/分
数量/个
800
700
600
500
400
300
200
100
250
答:小玲5分钟大约打了250个字。打750个字大约要15分钟。
画图方法:把表格中的对应数据写成数对,然后在方格纸上找出这些数对,依次连线画出图像。
表示正比例关系的图像特点:
1、图像是从横轴和纵轴的交点画出的一条射线。
2、横轴和纵轴表示的两种量的所有对应点都在这
条射线上。
画图表示成正比例的量
练一练 第2、3题
