冀教版 六年级数学下册3.3成反比例的量课件(17张PPT)
文档属性
| 名称 | 冀教版 六年级数学下册3.3成反比例的量课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 14:31:04 | ||
图片预览





文档简介
正比例 反比例
第3课时 成反比例的量
1.结合具体事例,经历认识和判断成反比例的量的过程。
2.知道反比例的意义,能判断两种量是否成反比例,能找出生活中成反比例的量的实例,并与同学进行交流。
3.对现实生活中成反比例关系的事物有好奇心,在判断成反比例的量的过程中,能进行有条理的思考。
【重点】能判断两种量是否成反比例。
【难点】理解反比例的意义,会判断两种量是否成反比例。
明明一共有40元钱,买下面几种练习本分别能买多少本?
{8A107856-5554-42FB-B03E-39F5DBC370BA} 练习本
第1种
第2种
第3种
本数
40
20
4
单价1元
单价2元
单价10元
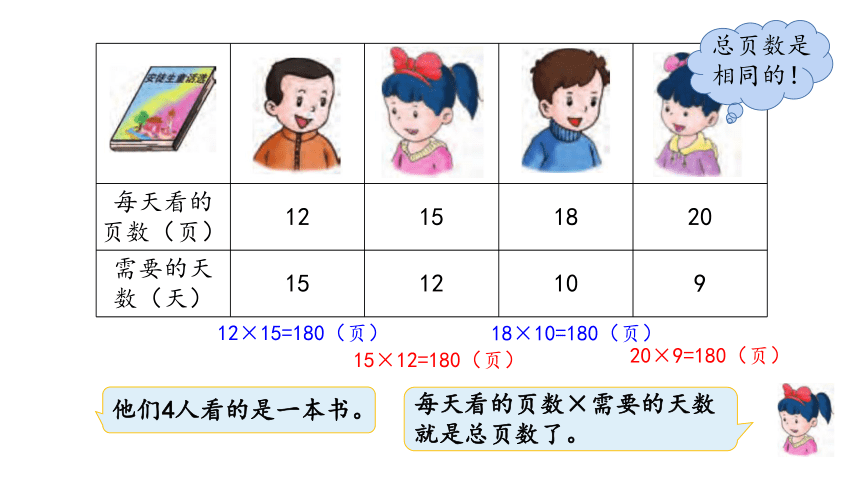
亮亮、红红、聪聪和丫丫各看一本《安徒生童话》。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
每天看的页数(页)
12
15
18
20
需要的天数(天)
15
12
10
9
从上表中你获取了什么信息?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
每天看的页数(页)
12
15
18
20
需要的天数(天)
15
12
10
9
他们4人看的是一本书。
总页数是相同的!
每天看的页数×需要的天数就是总页数了。
12×15=180(页)
15×12=180(页)
18×10=180(页)
20×9=180(页)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
每天看的页数(页)
12
15
18
20
需要的天数(天)
15
12
10
9
12×15=180(页)
15×12=180(页)
18×10=180(页)
20×9=180(页)
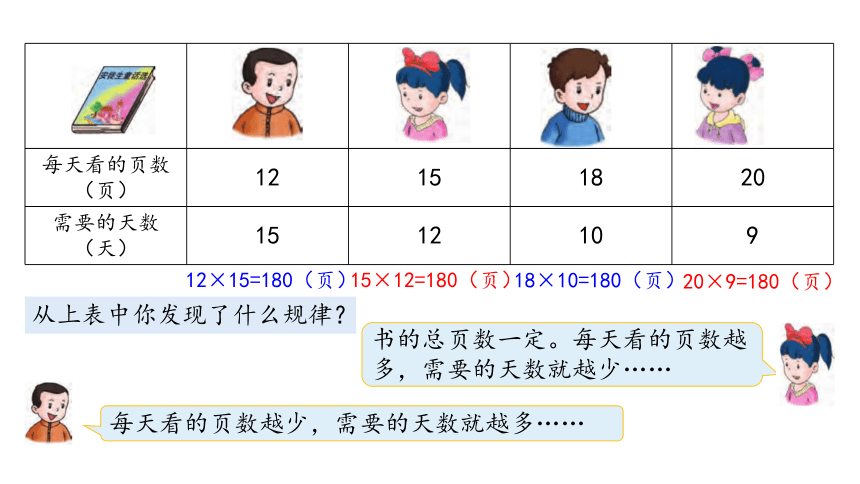
从上表中你发现了什么规律?
书的总页数一定。每天看的页数越多,需要的天数就越少……
每天看的页数越少,需要的天数就越多……
总页数是相同的!
每天看的页数×需要的天数=书的总页数
(一定)
在上面的问题中,看完一本书需要的天数和每天看书的页数是两种相关联的量。需要的天数随着每天看的页数的变化而变化,而且,每天看的页数和需要的天数的乘积一定(这本书的总页数一定)。我们说每天看的页数和需要的天数这两种量成反比例。
把一张10元的人民币分别换成同一种面值的零钱。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}面值
张数(张)
100
50
20
10
2
10元=100角
100÷2=50(张)
100÷5=20(张)
10÷1=10(张)
10÷5=2(张)
完成上表,你发现了什么规律?
零钱的面值越大,换的张数就越少。
把10元钱换成零钱,零钱的面值越小,换的张数就越多。
零钱的面值×零钱的张数=10元(总钱数)
零钱的面值与张数这两种量成反比例吗?为什么?
简单来说:当两种相关联的量对应的两个数的积一定时,那么这两种量成反比例。它们的关系叫做反比例关系。
像上面这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量。它们的关系叫做反比例关系。
成反比例,因为:零钱的面值×张数=总钱数(一定)
成反比例的两种量,也可以在方格纸上画图来表示。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}单价(元/件)
60
40
30
数量(件)
20
30
40
先用数对把对应数据表述出来。
(20,60)
横轴代表数量,纵轴代表单价。
(30,40)
(40,30)
在方格纸中找到对应数对,用平滑的曲线依次连接。
(20,60)
(30,40)
(40,30)
1.判断下面各题中的两种量是否成反比例,并说明理由。
(1)路程一定,汽车行驶的速度和需要的时间。
(2)聪聪拿12元钱买练习本,每本的价钱和购买的本数。
(3)三角形的面积一定,它的底和高。
速度和时间是两种相关联的量,行驶速度×需要的时间=路程(一定)
行驶速度和需要的时间成反比例。
每本的价钱和本数是两种相关联的量,每本的价钱×购买的本数=总钱数12元(一定)
每本的价钱和购买的本数成反比例。
总价
单价
数量
速度×时间=路程
单价×数量=总价
底×高÷2=三角形面积
三角形的底和高是两种相关联的量,底×高÷2=三角形面积(一定)
三角形的底和高成反比例。
判断下面各题中的两种量成什么比例,并说明理由。
(1)乒乓球总个数一定,每盒装的个数和需要的盒数。
(2)长方形的面积一定,长方形的长和宽。
(3)长方形的周长一定,长方形的长和宽。
每盒装的个数×需要的盒数=乒乓球总个数(一定)
每盒装的个数和需要的盒数成反比例。
长×宽=长方形的面积(一定)
长方形的长和宽成反比例。
比值一定,成正比例。
乘积一定,成反比例。
(长+宽)×2=长方形的周长
长方形的长和宽不成比例。
必须得是相关联的两种量的乘积或比值一定才成比例。
是两种相关联的量。
是两种相关联的量。
是两种相关联的量。
判断下面各题中的两种量成什么比例,并说明理由。
(4)轮船行驶的速度一定,行驶的路程和时间。
(5)每小时织布的米数一定,织布的总米数和时间。
(6)全班人数一定,男生人数和女生人数。
路程
时间
=速度(一定)
行驶的路程和时间成正比例。
总米数
时间
=每小时织布的米数(一定)
织布的总米数和时间成正比例。
男生人数+女生人数=全班总人数
男生人数和女生人数不成比例。
和一定,不成比例。
是两种相关联的量。
是两种相关联的量。
是两种相关联的量。
服装厂接到一批订单,经理做了如下生产方案:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}每天加工的件数(件)
10
20
30
40
50
60
需要的天数(天)
60
30
(1)照上面计算,完成上表。
20
15
12
10
60×10=600(件)
20×30=600(件)
每天加工的件数×需要的天数=600(一定)
600÷30=20(件)
600÷40=15(件)
600÷50=12(件)
600÷60=10(件)
服装厂接到一批订单,经理做了如下生产方案:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}每天加工的件数(件)
10
20
30
40
50
60
需要的天数(天)
60
30
(2)每天加工的件数和需要的天数,这两种量成什么比例?
20
15
12
10
答:每天加工的件数和需要的天数成反比例。因为这是两个相关联的量,且每天加工的件数×需要的天数=订单总数量(一定)
所以订单总数量一定,每天加工的件数和需要的天数成反比例。
当两种相关联的量对应的两个数的积一定时,
那么这两种量成反比例。它们的关系叫做反比例关系。
比值一定,成正比例。乘积一定,成反比例。
成反比例的量
练一练 第2、3题
第3课时 成反比例的量
1.结合具体事例,经历认识和判断成反比例的量的过程。
2.知道反比例的意义,能判断两种量是否成反比例,能找出生活中成反比例的量的实例,并与同学进行交流。
3.对现实生活中成反比例关系的事物有好奇心,在判断成反比例的量的过程中,能进行有条理的思考。
【重点】能判断两种量是否成反比例。
【难点】理解反比例的意义,会判断两种量是否成反比例。
明明一共有40元钱,买下面几种练习本分别能买多少本?
{8A107856-5554-42FB-B03E-39F5DBC370BA} 练习本
第1种
第2种
第3种
本数
40
20
4
单价1元
单价2元
单价10元
亮亮、红红、聪聪和丫丫各看一本《安徒生童话》。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
每天看的页数(页)
12
15
18
20
需要的天数(天)
15
12
10
9
从上表中你获取了什么信息?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
每天看的页数(页)
12
15
18
20
需要的天数(天)
15
12
10
9
他们4人看的是一本书。
总页数是相同的!
每天看的页数×需要的天数就是总页数了。
12×15=180(页)
15×12=180(页)
18×10=180(页)
20×9=180(页)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
每天看的页数(页)
12
15
18
20
需要的天数(天)
15
12
10
9
12×15=180(页)
15×12=180(页)
18×10=180(页)
20×9=180(页)
从上表中你发现了什么规律?
书的总页数一定。每天看的页数越多,需要的天数就越少……
每天看的页数越少,需要的天数就越多……
总页数是相同的!
每天看的页数×需要的天数=书的总页数
(一定)
在上面的问题中,看完一本书需要的天数和每天看书的页数是两种相关联的量。需要的天数随着每天看的页数的变化而变化,而且,每天看的页数和需要的天数的乘积一定(这本书的总页数一定)。我们说每天看的页数和需要的天数这两种量成反比例。
把一张10元的人民币分别换成同一种面值的零钱。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}面值
张数(张)
100
50
20
10
2
10元=100角
100÷2=50(张)
100÷5=20(张)
10÷1=10(张)
10÷5=2(张)
完成上表,你发现了什么规律?
零钱的面值越大,换的张数就越少。
把10元钱换成零钱,零钱的面值越小,换的张数就越多。
零钱的面值×零钱的张数=10元(总钱数)
零钱的面值与张数这两种量成反比例吗?为什么?
简单来说:当两种相关联的量对应的两个数的积一定时,那么这两种量成反比例。它们的关系叫做反比例关系。
像上面这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量。它们的关系叫做反比例关系。
成反比例,因为:零钱的面值×张数=总钱数(一定)
成反比例的两种量,也可以在方格纸上画图来表示。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}单价(元/件)
60
40
30
数量(件)
20
30
40
先用数对把对应数据表述出来。
(20,60)
横轴代表数量,纵轴代表单价。
(30,40)
(40,30)
在方格纸中找到对应数对,用平滑的曲线依次连接。
(20,60)
(30,40)
(40,30)
1.判断下面各题中的两种量是否成反比例,并说明理由。
(1)路程一定,汽车行驶的速度和需要的时间。
(2)聪聪拿12元钱买练习本,每本的价钱和购买的本数。
(3)三角形的面积一定,它的底和高。
速度和时间是两种相关联的量,行驶速度×需要的时间=路程(一定)
行驶速度和需要的时间成反比例。
每本的价钱和本数是两种相关联的量,每本的价钱×购买的本数=总钱数12元(一定)
每本的价钱和购买的本数成反比例。
总价
单价
数量
速度×时间=路程
单价×数量=总价
底×高÷2=三角形面积
三角形的底和高是两种相关联的量,底×高÷2=三角形面积(一定)
三角形的底和高成反比例。
判断下面各题中的两种量成什么比例,并说明理由。
(1)乒乓球总个数一定,每盒装的个数和需要的盒数。
(2)长方形的面积一定,长方形的长和宽。
(3)长方形的周长一定,长方形的长和宽。
每盒装的个数×需要的盒数=乒乓球总个数(一定)
每盒装的个数和需要的盒数成反比例。
长×宽=长方形的面积(一定)
长方形的长和宽成反比例。
比值一定,成正比例。
乘积一定,成反比例。
(长+宽)×2=长方形的周长
长方形的长和宽不成比例。
必须得是相关联的两种量的乘积或比值一定才成比例。
是两种相关联的量。
是两种相关联的量。
是两种相关联的量。
判断下面各题中的两种量成什么比例,并说明理由。
(4)轮船行驶的速度一定,行驶的路程和时间。
(5)每小时织布的米数一定,织布的总米数和时间。
(6)全班人数一定,男生人数和女生人数。
路程
时间
=速度(一定)
行驶的路程和时间成正比例。
总米数
时间
=每小时织布的米数(一定)
织布的总米数和时间成正比例。
男生人数+女生人数=全班总人数
男生人数和女生人数不成比例。
和一定,不成比例。
是两种相关联的量。
是两种相关联的量。
是两种相关联的量。
服装厂接到一批订单,经理做了如下生产方案:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}每天加工的件数(件)
10
20
30
40
50
60
需要的天数(天)
60
30
(1)照上面计算,完成上表。
20
15
12
10
60×10=600(件)
20×30=600(件)
每天加工的件数×需要的天数=600(一定)
600÷30=20(件)
600÷40=15(件)
600÷50=12(件)
600÷60=10(件)
服装厂接到一批订单,经理做了如下生产方案:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}每天加工的件数(件)
10
20
30
40
50
60
需要的天数(天)
60
30
(2)每天加工的件数和需要的天数,这两种量成什么比例?
20
15
12
10
答:每天加工的件数和需要的天数成反比例。因为这是两个相关联的量,且每天加工的件数×需要的天数=订单总数量(一定)
所以订单总数量一定,每天加工的件数和需要的天数成反比例。
当两种相关联的量对应的两个数的积一定时,
那么这两种量成反比例。它们的关系叫做反比例关系。
比值一定,成正比例。乘积一定,成反比例。
成反比例的量
练一练 第2、3题
