冀教版 六年级数学下册3.4整理与复习课件(18张PPT)
文档属性
| 名称 | 冀教版 六年级数学下册3.4整理与复习课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 00:00:00 | ||
图片预览




文档简介
正比例 反比例
第4课时 整理与复习
1.结合具体事例,经历讨论和总结正、反比例关系式及字母表达式的过程。
2.在常见数量关系的三种量中,知道某一种量一定,另外两种量成什么比例关系;理解正、反比例的字母表达式和含义。
3.在讨论和判断正、反比例量的过程中,能进行有条理的思考,能清楚地表达判断和思考的过程与结果。
【重点】加深对正、反比例知识的理解,掌握成正、反比例的字母表达式。
【难点】加深对正、反比例知识的理解,掌握成正、反比例的字母表达式。
我们先来回顾一下本单元学过的知识吧。
当两种相关联的量对应的两个数的比值一定时,那么这两种量成正比例。它们的关系叫做正比例关系。
正比例
成正比例的两种量的图像是从横轴和纵轴的交点画出的一条射线。
我们先来回顾一下本单元学过的知识吧。
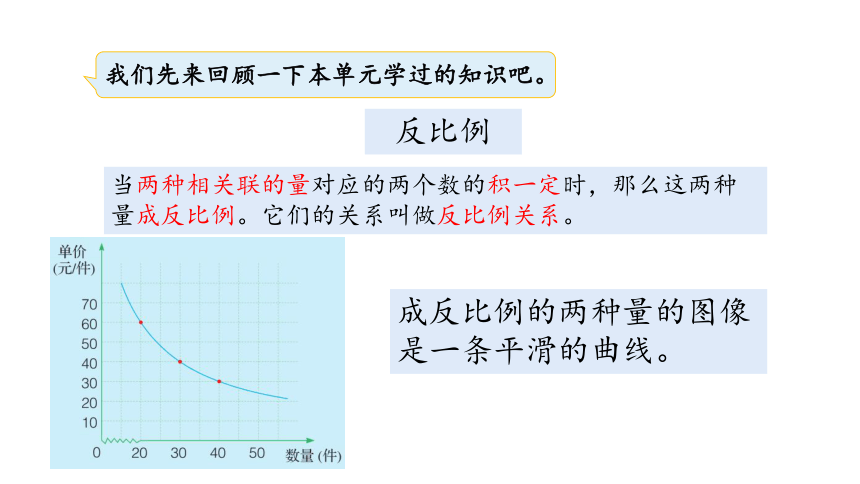
当两种相关联的量对应的两个数的积一定时,那么这两种量成反比例。它们的关系叫做反比例关系。
反比例
成反比例的两种量的图像是一条平滑的曲线。
让我们总结一下正比例和反比例知识的异同吧。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
正比例
反比例
相
同
点
(1)都有两种相关联的量;
(2)都是一种量随着另一种量的变化而变化;
(3)两种相关联的量变化后的结果(商或积)都是一定的。
相
同
点
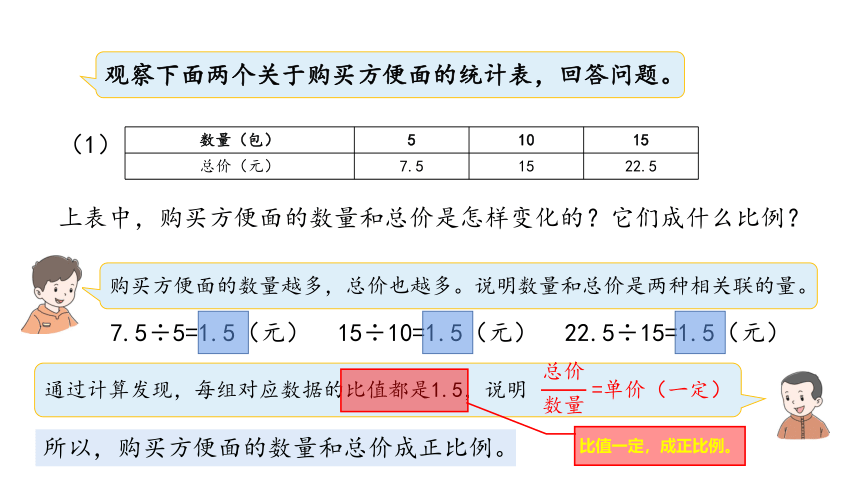
观察下面两个关于购买方便面的统计表,回答问题。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}数量(包)
5
10
15
总价(元)
7.5
15
22.5
上表中,购买方便面的数量和总价是怎样变化的?它们成什么比例?
(1)
7.5÷5=1.5(元)
购买方便面的数量越多,总价也越多。说明数量和总价是两种相关联的量。
15÷10=1.5(元)
22.5÷15=1.5(元)
通过计算发现,每组对应数据的比值都是1.5,说明 =单价(一定)
总价
数量
所以,购买方便面的数量和总价成正比例。
比值一定,成正比例。
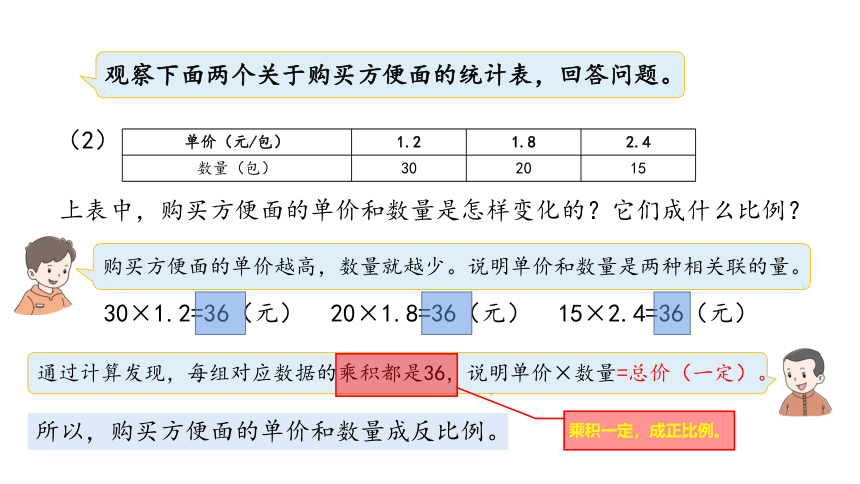
观察下面两个关于购买方便面的统计表,回答问题。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}单价(元/包)
1.2
1.8
2.4
数量(包)
30
20
15
上表中,购买方便面的单价和数量是怎样变化的?它们成什么比例?
(2)
30×1.2=36(元)
购买方便面的单价越高,数量就越少。说明单价和数量是两种相关联的量。
20×1.8=36(元)
15×2.4=36(元)
通过计算发现,每组对应数据的乘积都是36,说明单价×数量=总价(一定)。
所以,购买方便面的单价和数量成反比例。
乘积一定,成正比例。
议一议
当总价一定时,单价和数量成什么比例?
当数量一定时,总价和单价成什么比例?
当单价一定时,总价和数量成什么比例?
单价×数量=总价(一定)
当总价一定时,单价和数量成反比例。
乘积一定,成反比例
当数量一定时,总价和单价成正比例。
比值一定,成正比例
=数量(一定)
总价
单价
比值一定,成正比例
总价
数量
=单价(一定)
当单价一定时,总价和数量成正比例。
在一次自行车越野赛中,小明骑车的时间与路程如下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间(分)
8
10
20
40
60
路程(千米)
2
2.5
5
10
15
(1)路程和时间成什么比例?
通过计算发现,每组对应数据的比值都是4,说明 =速度(一定)。
路程
时间
另外路程和时间是两种相关联的量。所以,路程和时间成正比例。
比值一定,成正比例。
8÷2= 4(元)
10÷2.5= 4(元)
20÷5= 4(元)
40÷10= 4(元)
60÷15= 4(元)
时间、路程和速度这三种量,在什么情况下成正比例,什么情况下成反比例?说明理由。
时间×速度=路程(一定)
当路程一定时,时间和速度成反比例。
当时间一定时,路程和速度成正比例。
=时间(一定)
路程
速度
路程
时间
=速度(一定)
当速度一定时,路程和时间成正比例。
如果用字母x和y表示两种相关联的量,用k表示一定的量,成正比例、反比例的关系可以分别用下面的式子表示。
正比例
x ? y=k
=k
y
x
反比例
火眼金睛。
(1)人的年龄和体重不成比例关系。 ( )
(2)订同一种杂志的份数和总钱数成正比例。 ( )
(3)被除数一定,除数和商成反比例。 ( )
(4)圆的半径和面积成正比例。 ( )
√
不是两种相关联的量。
是两种相关联的量。
√
是两种相关联的量。
√
是两种相关联的量。
×
=每本的钱数(一定)
总钱数
份数
被除数=商×除数
圆的面积=π×r?,所以圆的半径和面积不成比例。
汽车每次运货的吨数、运货的次数和运货的总吨数这三种量,在什么情况下成正比例,什么情况下成反比例?
每次运货的吨数×运货的次数=运货的总吨数(一定)
当运货的总吨数一定时,每次运货的吨数和运货的次数成反比例。
当运货的次数一定时,运货的总吨数和每次运货的吨数成正比例。
=运货的次数(一定)
运货的总吨数
每次运货的吨数
当每次运货的吨数一定时,运货的总吨数和运货的次数成正比例。
=每次运货的吨数(一定)
运货的总吨数
运货的次数
一个榨油厂用4台同样的榨油机每天榨油36吨。
(1)题中哪两种量是相关联的量?哪种量是一定的?
说明每台榨油机每天榨油的吨数一样。
也就是每台榨油机每天榨油的吨数是一定的。
榨油机的台数和榨油的吨数是相关联的量。
一个榨油厂用4台同样的榨油机每天榨油36吨。
(2)榨油机的台数和每天榨油的吨数成正比例吗?为什么?
成正比例,因为每天榨油的吨数和榨油机的台数的比值是一定的,都是9 。
=每台榨油机每天榨油的吨数(一定)
每天榨油的吨数
榨油机的台数
也就是:
所以,榨油机的台数和每天榨油的吨数成正比例。
一个榨油厂用4台同样的榨油机每天榨油36吨。
(3)照这样计算,6台这样的榨油机每天榨油多少吨?
36÷ 4 =9 (吨)
9 × 6=54(吨)
答: 6台这样的榨油机每天榨油54吨。
(4)把榨油机的台数和每天榨油
的吨数在右面的方格纸上表示出来。
1台榨油机可榨油9吨,
2台榨油机可榨油18吨,
3台榨油机可榨油27吨,
4台榨油机可榨油36吨。
当两种相关联的量对应的两个数的比值一定时,那么这两种量成正比例。它们的关系叫做正比例关系。用
字母表示为: 。
=k
y
x
当两种相关联的量对应的两个数的积一定时,那么这两种量成反比例。它们的关系叫做反比例关系。用字母表示为: 。
x ? y=k
整理与复习
练一练 第3、4题
第4课时 整理与复习
1.结合具体事例,经历讨论和总结正、反比例关系式及字母表达式的过程。
2.在常见数量关系的三种量中,知道某一种量一定,另外两种量成什么比例关系;理解正、反比例的字母表达式和含义。
3.在讨论和判断正、反比例量的过程中,能进行有条理的思考,能清楚地表达判断和思考的过程与结果。
【重点】加深对正、反比例知识的理解,掌握成正、反比例的字母表达式。
【难点】加深对正、反比例知识的理解,掌握成正、反比例的字母表达式。
我们先来回顾一下本单元学过的知识吧。
当两种相关联的量对应的两个数的比值一定时,那么这两种量成正比例。它们的关系叫做正比例关系。
正比例
成正比例的两种量的图像是从横轴和纵轴的交点画出的一条射线。
我们先来回顾一下本单元学过的知识吧。
当两种相关联的量对应的两个数的积一定时,那么这两种量成反比例。它们的关系叫做反比例关系。
反比例
成反比例的两种量的图像是一条平滑的曲线。
让我们总结一下正比例和反比例知识的异同吧。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
正比例
反比例
相
同
点
(1)都有两种相关联的量;
(2)都是一种量随着另一种量的变化而变化;
(3)两种相关联的量变化后的结果(商或积)都是一定的。
相
同
点
观察下面两个关于购买方便面的统计表,回答问题。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}数量(包)
5
10
15
总价(元)
7.5
15
22.5
上表中,购买方便面的数量和总价是怎样变化的?它们成什么比例?
(1)
7.5÷5=1.5(元)
购买方便面的数量越多,总价也越多。说明数量和总价是两种相关联的量。
15÷10=1.5(元)
22.5÷15=1.5(元)
通过计算发现,每组对应数据的比值都是1.5,说明 =单价(一定)
总价
数量
所以,购买方便面的数量和总价成正比例。
比值一定,成正比例。
观察下面两个关于购买方便面的统计表,回答问题。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}单价(元/包)
1.2
1.8
2.4
数量(包)
30
20
15
上表中,购买方便面的单价和数量是怎样变化的?它们成什么比例?
(2)
30×1.2=36(元)
购买方便面的单价越高,数量就越少。说明单价和数量是两种相关联的量。
20×1.8=36(元)
15×2.4=36(元)
通过计算发现,每组对应数据的乘积都是36,说明单价×数量=总价(一定)。
所以,购买方便面的单价和数量成反比例。
乘积一定,成正比例。
议一议
当总价一定时,单价和数量成什么比例?
当数量一定时,总价和单价成什么比例?
当单价一定时,总价和数量成什么比例?
单价×数量=总价(一定)
当总价一定时,单价和数量成反比例。
乘积一定,成反比例
当数量一定时,总价和单价成正比例。
比值一定,成正比例
=数量(一定)
总价
单价
比值一定,成正比例
总价
数量
=单价(一定)
当单价一定时,总价和数量成正比例。
在一次自行车越野赛中,小明骑车的时间与路程如下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间(分)
8
10
20
40
60
路程(千米)
2
2.5
5
10
15
(1)路程和时间成什么比例?
通过计算发现,每组对应数据的比值都是4,说明 =速度(一定)。
路程
时间
另外路程和时间是两种相关联的量。所以,路程和时间成正比例。
比值一定,成正比例。
8÷2= 4(元)
10÷2.5= 4(元)
20÷5= 4(元)
40÷10= 4(元)
60÷15= 4(元)
时间、路程和速度这三种量,在什么情况下成正比例,什么情况下成反比例?说明理由。
时间×速度=路程(一定)
当路程一定时,时间和速度成反比例。
当时间一定时,路程和速度成正比例。
=时间(一定)
路程
速度
路程
时间
=速度(一定)
当速度一定时,路程和时间成正比例。
如果用字母x和y表示两种相关联的量,用k表示一定的量,成正比例、反比例的关系可以分别用下面的式子表示。
正比例
x ? y=k
=k
y
x
反比例
火眼金睛。
(1)人的年龄和体重不成比例关系。 ( )
(2)订同一种杂志的份数和总钱数成正比例。 ( )
(3)被除数一定,除数和商成反比例。 ( )
(4)圆的半径和面积成正比例。 ( )
√
不是两种相关联的量。
是两种相关联的量。
√
是两种相关联的量。
√
是两种相关联的量。
×
=每本的钱数(一定)
总钱数
份数
被除数=商×除数
圆的面积=π×r?,所以圆的半径和面积不成比例。
汽车每次运货的吨数、运货的次数和运货的总吨数这三种量,在什么情况下成正比例,什么情况下成反比例?
每次运货的吨数×运货的次数=运货的总吨数(一定)
当运货的总吨数一定时,每次运货的吨数和运货的次数成反比例。
当运货的次数一定时,运货的总吨数和每次运货的吨数成正比例。
=运货的次数(一定)
运货的总吨数
每次运货的吨数
当每次运货的吨数一定时,运货的总吨数和运货的次数成正比例。
=每次运货的吨数(一定)
运货的总吨数
运货的次数
一个榨油厂用4台同样的榨油机每天榨油36吨。
(1)题中哪两种量是相关联的量?哪种量是一定的?
说明每台榨油机每天榨油的吨数一样。
也就是每台榨油机每天榨油的吨数是一定的。
榨油机的台数和榨油的吨数是相关联的量。
一个榨油厂用4台同样的榨油机每天榨油36吨。
(2)榨油机的台数和每天榨油的吨数成正比例吗?为什么?
成正比例,因为每天榨油的吨数和榨油机的台数的比值是一定的,都是9 。
=每台榨油机每天榨油的吨数(一定)
每天榨油的吨数
榨油机的台数
也就是:
所以,榨油机的台数和每天榨油的吨数成正比例。
一个榨油厂用4台同样的榨油机每天榨油36吨。
(3)照这样计算,6台这样的榨油机每天榨油多少吨?
36÷ 4 =9 (吨)
9 × 6=54(吨)
答: 6台这样的榨油机每天榨油54吨。
(4)把榨油机的台数和每天榨油
的吨数在右面的方格纸上表示出来。
1台榨油机可榨油9吨,
2台榨油机可榨油18吨,
3台榨油机可榨油27吨,
4台榨油机可榨油36吨。
当两种相关联的量对应的两个数的比值一定时,那么这两种量成正比例。它们的关系叫做正比例关系。用
字母表示为: 。
=k
y
x
当两种相关联的量对应的两个数的积一定时,那么这两种量成反比例。它们的关系叫做反比例关系。用字母表示为: 。
x ? y=k
整理与复习
练一练 第3、4题
