垂径定理(2)
图片预览
文档简介
(共21张PPT)
A
B
C
D
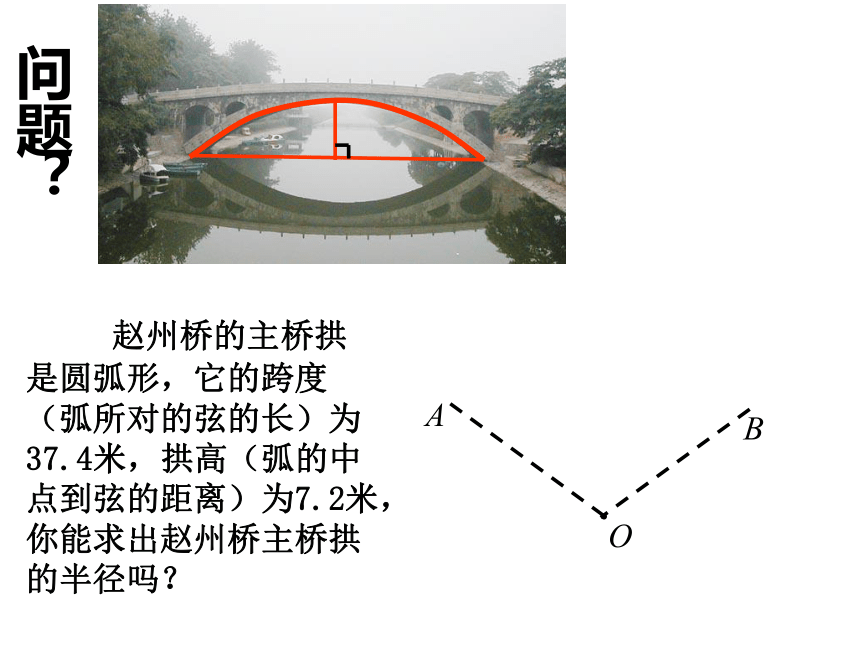
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?
问题?
O
A
B
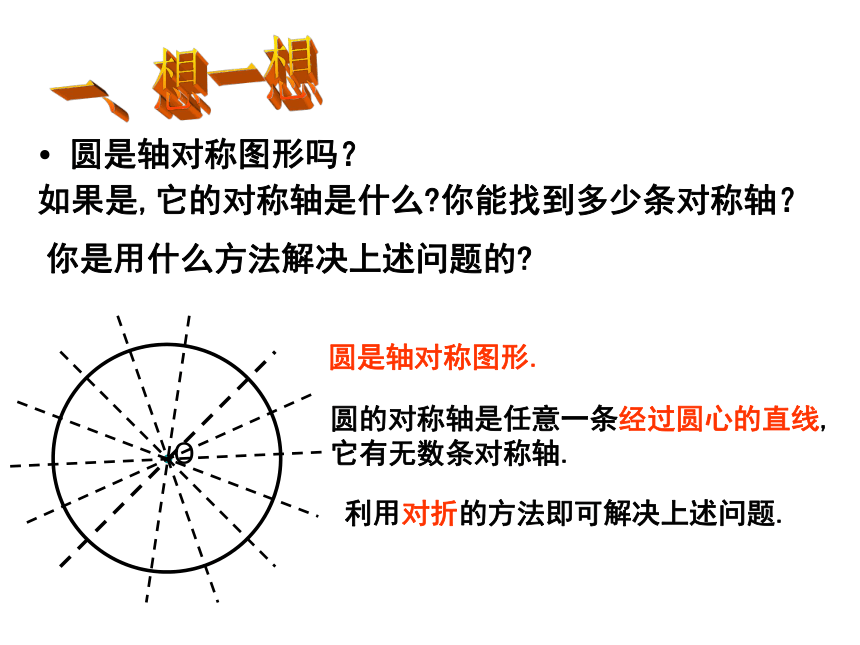
圆是轴对称图形吗?
如果是,它的对称轴是什么 你能找到多少条对称轴?
你是用什么方法解决上述问题的
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
利用对折的方法即可解决上述问题.
●O
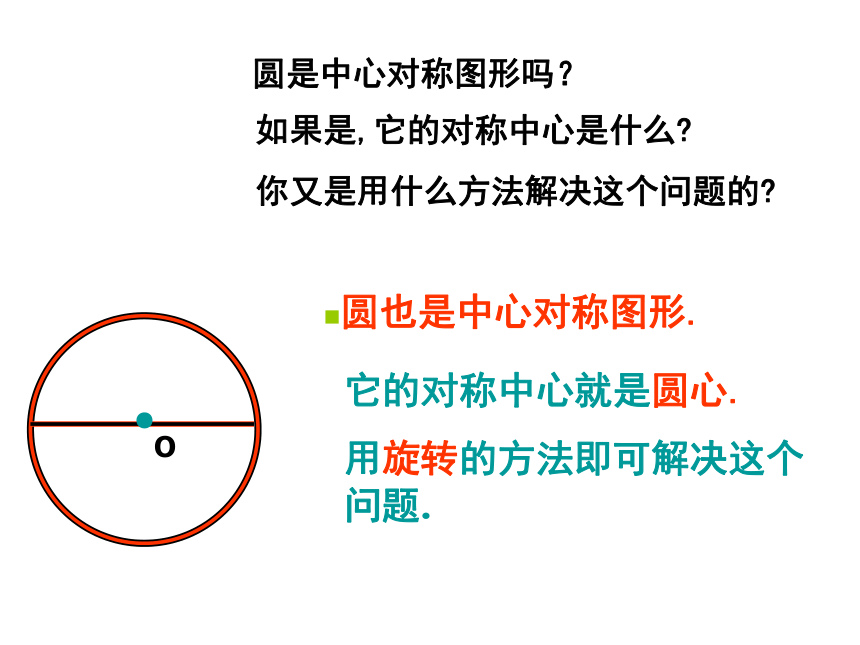
圆也是中心对称图形.
它的对称中心就是圆心.
用旋转的方法即可解决这个问题.
圆是中心对称图形吗?
如果是,它的对称中心是什么
你又是用什么方法解决这个问题的
O
●
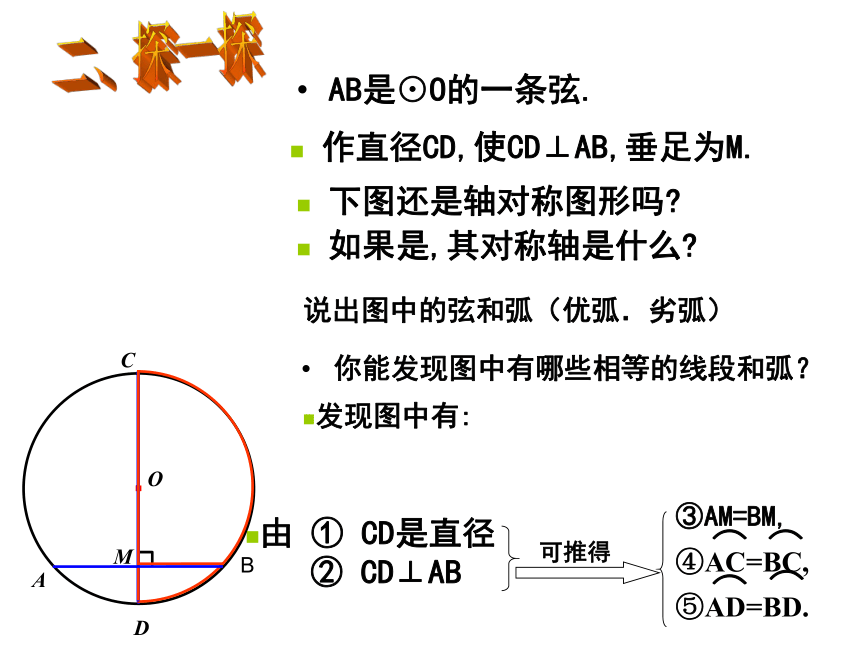
③AM=BM,
AB是⊙O的一条弦.
你能发现图中有哪些相等的线段和弧?
作直径CD,使CD⊥AB,垂足为M.
下图还是轴对称图形吗
如果是,其对称轴是什么
发现图中有:
由 ① CD是直径
② CD⊥AB
可推得
说出图中的弦和弧(优弧.劣弧)
·
O
M
C
D
A
B
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
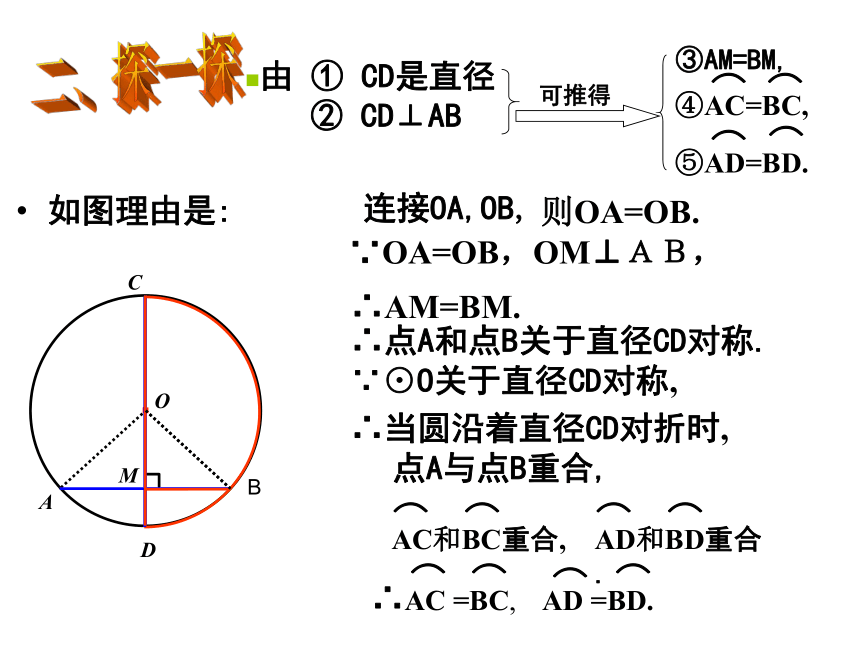
如图理由是:
连接OA,OB,
则OA=OB.
∵OA=OB,OM⊥AB,
∴AM=BM.
∴点A和点B关于直径CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,
点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
③AM=BM,
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
·
O
A
C
D
M
B
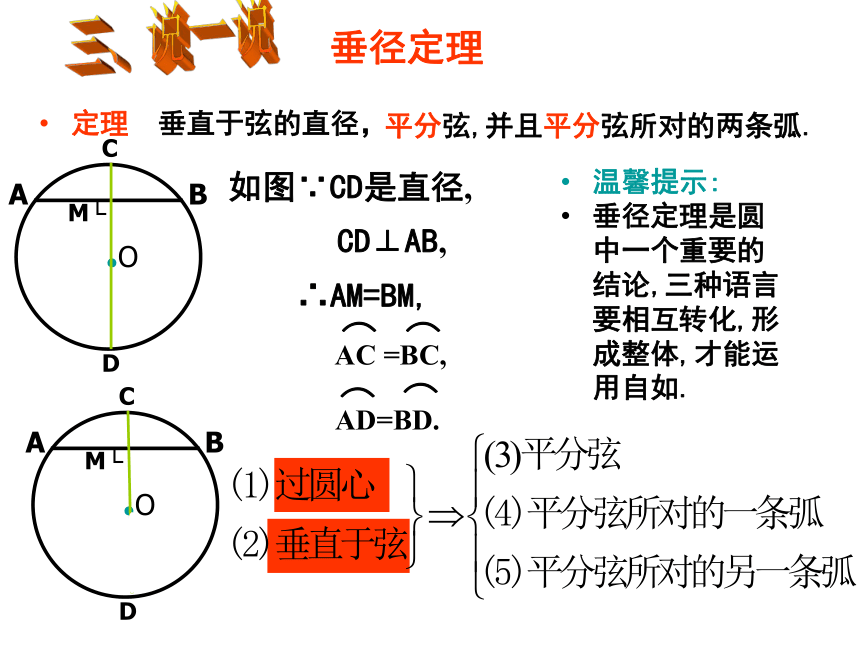
定理 垂直于弦的直径,
温馨提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
●O
A
B
C
D
M└
CD⊥AB,
如图∵CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
平分弦,并且平分弦所对的两条弧.
垂径定理
●O
A
B
C
D
M└
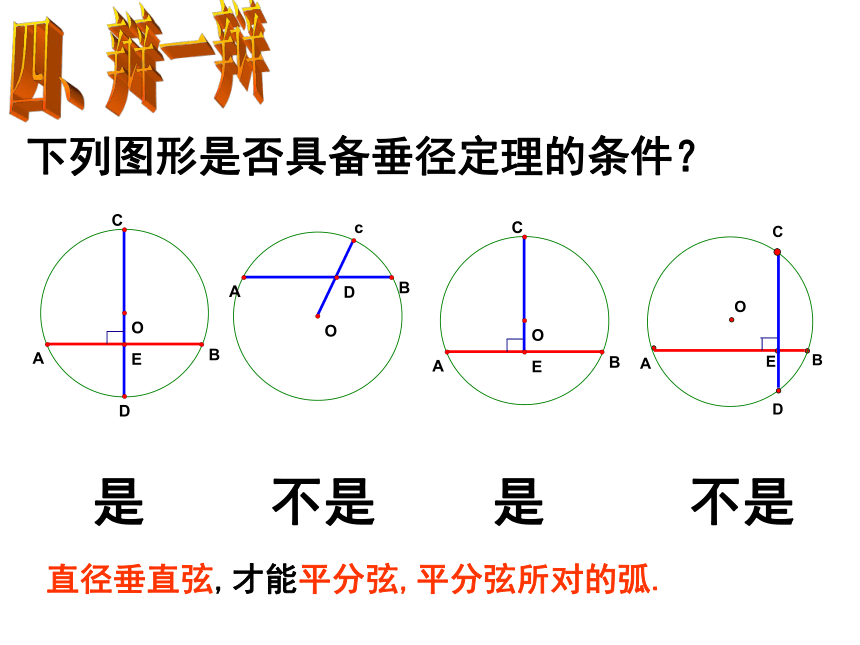
下列图形是否具备垂径定理的条件?
是
不是
是
不是
O
E
D
C
A
B
直径垂直弦,才能平分弦,平分弦所对的弧.
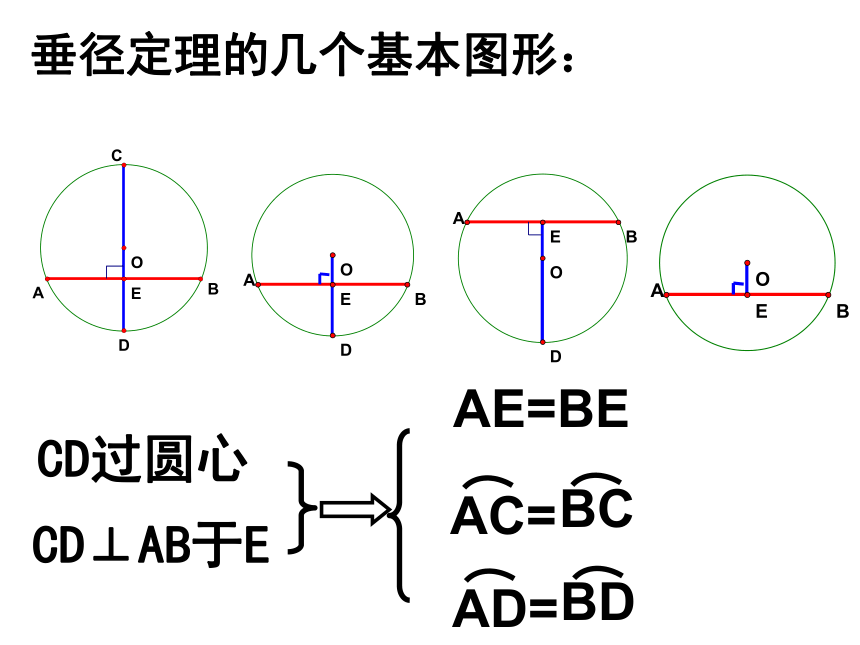
垂径定理的几个基本图形:
CD过圆心
CD⊥AB于E
AE=BE
AC=
BC
AD=
BD
E
O
B
D
A
O
B
D
A
E
O
B
A
E
不是直径
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
B
A
O
C
D
E
A
C
B
D
O
(不是直径)
例1.已知:如图,弦AB是⊙O中一条非直径弦,D为弦AB 的中点,连接OD ,AB=6cm ,OD=4cm. 求⊙O 的半径.
D
O
B
A
解:连接OA
∵D为 弦AB 的中点
∴OD⊥A B,AD= AB=3cm
在Rt △ AOD 中, AO2=OD2+AD2
设⊙O 的半径为r,则
r2=42+32
得r = 5
答: ⊙O 的半径OA为5cm.
例2.如图,弦AB的长为 8 cm,圆心O到 AB 的距离为 3 cm,求⊙O的半径.
注意书写格式
O
A
B
E
答:⊙O 的半径为5cm.
在Rt △ AOE 中
解:作OE⊥AB于E点,连接OA.
变1.在⊙O中,直径为 10 cm,弦 AB的长为 8 cm, 则圆心O到AB的距离 .
变2.在⊙O中,直径为 10 cm,圆心O到AB的距离为 3 cm,则弦AB的长为 .
圆的半径为R,弦长为 a,弦心距为d,则 R 、a、d满
足关系式_________
求圆中有关线段的长度时,常借助垂径定理转化
为直角三角形,从而利用勾股定理来解决问题.
3cm
8cm
37.4m
7.2m
A
B
O
C
E
答:赵州桥的主桥拱半径约为27.9m.
如图用 表示主桥拱,设 所在圆的圆心为O,半径为r.经过圆心O作弦AB的垂线OC,D为垂足,OC与 相交于点C,根据前面的结论,D是AB的中点,C是 的中点,CD就是拱高. 在图中,
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?
解决问题
如图,已知两个同心圆,大圆的弦AB与小圆交于C,D
求证:AC=BD
1、圆是轴对称图形,其对称轴是每一条直径所在的直线或经过圆
心的每一条直线。
2、垂径定理
CD平分弧ADB
CD平分弦AB
CD平分弧ACB
CD过圆心
CD⊥AB
C
D
B
A
O
3、在⊙ O中,若⊙ O的半径r、圆心到弦的距离d、弦长a中,
任意知道两个量,可根据垂径定理求出第三个量:
垂径定理推论:
如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.
D
·
O
A
B
C
E
如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____.最大值为____________.
3
5
B
A
O
C
D
1、同心圆O中,大圆的直径AB交小圆于点C、D,请问AC=BD吗?
2、如果把AB向下平移,弦AB仍然交小圆于点C、D,此时图中还有哪些相等的线段?为什么?
应用:
B
A
O
C
D
E
若两圆半径分别为5cm和 ,弦AB=8cm,
则AC= cm.
1
在圆中研究有关弦的问题时,常过圆心作垂直于弦的垂线段,利用垂径定理来证明线段相等、弧相等,利用勾股定理列方程进行计算.
3.已知⊙O的直径是50 cm,⊙O的两条平行弦AB=40 cm ,CD=48cm,
求弦AB与CD之间的距离。
.
A
E
B
O
C
D
20
15
25
25
24
7
.
A
E
B
O
C
D
F
F
AB、CD在点O两侧
EF=OE+OF=15+7=22
AB、CD在点O同侧
EF=OE-OF=15-7=8
过点O作直线OE⊥AB,交CD于F。
不学自知,不问自晓,
古今行事,未之有也.
A
B
C
D
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?
问题?
O
A
B
圆是轴对称图形吗?
如果是,它的对称轴是什么 你能找到多少条对称轴?
你是用什么方法解决上述问题的
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
利用对折的方法即可解决上述问题.
●O
圆也是中心对称图形.
它的对称中心就是圆心.
用旋转的方法即可解决这个问题.
圆是中心对称图形吗?
如果是,它的对称中心是什么
你又是用什么方法解决这个问题的
O
●
③AM=BM,
AB是⊙O的一条弦.
你能发现图中有哪些相等的线段和弧?
作直径CD,使CD⊥AB,垂足为M.
下图还是轴对称图形吗
如果是,其对称轴是什么
发现图中有:
由 ① CD是直径
② CD⊥AB
可推得
说出图中的弦和弧(优弧.劣弧)
·
O
M
C
D
A
B
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
如图理由是:
连接OA,OB,
则OA=OB.
∵OA=OB,OM⊥AB,
∴AM=BM.
∴点A和点B关于直径CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,
点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
③AM=BM,
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
·
O
A
C
D
M
B
定理 垂直于弦的直径,
温馨提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
●O
A
B
C
D
M└
CD⊥AB,
如图∵CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
平分弦,并且平分弦所对的两条弧.
垂径定理
●O
A
B
C
D
M└
下列图形是否具备垂径定理的条件?
是
不是
是
不是
O
E
D
C
A
B
直径垂直弦,才能平分弦,平分弦所对的弧.
垂径定理的几个基本图形:
CD过圆心
CD⊥AB于E
AE=BE
AC=
BC
AD=
BD
E
O
B
D
A
O
B
D
A
E
O
B
A
E
不是直径
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
B
A
O
C
D
E
A
C
B
D
O
(不是直径)
例1.已知:如图,弦AB是⊙O中一条非直径弦,D为弦AB 的中点,连接OD ,AB=6cm ,OD=4cm. 求⊙O 的半径.
D
O
B
A
解:连接OA
∵D为 弦AB 的中点
∴OD⊥A B,AD= AB=3cm
在Rt △ AOD 中, AO2=OD2+AD2
设⊙O 的半径为r,则
r2=42+32
得r = 5
答: ⊙O 的半径OA为5cm.
例2.如图,弦AB的长为 8 cm,圆心O到 AB 的距离为 3 cm,求⊙O的半径.
注意书写格式
O
A
B
E
答:⊙O 的半径为5cm.
在Rt △ AOE 中
解:作OE⊥AB于E点,连接OA.
变1.在⊙O中,直径为 10 cm,弦 AB的长为 8 cm, 则圆心O到AB的距离 .
变2.在⊙O中,直径为 10 cm,圆心O到AB的距离为 3 cm,则弦AB的长为 .
圆的半径为R,弦长为 a,弦心距为d,则 R 、a、d满
足关系式_________
求圆中有关线段的长度时,常借助垂径定理转化
为直角三角形,从而利用勾股定理来解决问题.
3cm
8cm
37.4m
7.2m
A
B
O
C
E
答:赵州桥的主桥拱半径约为27.9m.
如图用 表示主桥拱,设 所在圆的圆心为O,半径为r.经过圆心O作弦AB的垂线OC,D为垂足,OC与 相交于点C,根据前面的结论,D是AB的中点,C是 的中点,CD就是拱高. 在图中,
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?
解决问题
如图,已知两个同心圆,大圆的弦AB与小圆交于C,D
求证:AC=BD
1、圆是轴对称图形,其对称轴是每一条直径所在的直线或经过圆
心的每一条直线。
2、垂径定理
CD平分弧ADB
CD平分弦AB
CD平分弧ACB
CD过圆心
CD⊥AB
C
D
B
A
O
3、在⊙ O中,若⊙ O的半径r、圆心到弦的距离d、弦长a中,
任意知道两个量,可根据垂径定理求出第三个量:
垂径定理推论:
如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.
D
·
O
A
B
C
E
如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____.最大值为____________.
3
5
B
A
O
C
D
1、同心圆O中,大圆的直径AB交小圆于点C、D,请问AC=BD吗?
2、如果把AB向下平移,弦AB仍然交小圆于点C、D,此时图中还有哪些相等的线段?为什么?
应用:
B
A
O
C
D
E
若两圆半径分别为5cm和 ,弦AB=8cm,
则AC= cm.
1
在圆中研究有关弦的问题时,常过圆心作垂直于弦的垂线段,利用垂径定理来证明线段相等、弧相等,利用勾股定理列方程进行计算.
3.已知⊙O的直径是50 cm,⊙O的两条平行弦AB=40 cm ,CD=48cm,
求弦AB与CD之间的距离。
.
A
E
B
O
C
D
20
15
25
25
24
7
.
A
E
B
O
C
D
F
F
AB、CD在点O两侧
EF=OE+OF=15+7=22
AB、CD在点O同侧
EF=OE-OF=15-7=8
过点O作直线OE⊥AB,交CD于F。
不学自知,不问自晓,
古今行事,未之有也.
同课章节目录
