人教版八年级下册第16章16.2 分式的运算课时同步训练
文档属性
| 名称 | 人教版八年级下册第16章16.2 分式的运算课时同步训练 |

|
|
| 格式 | rar | ||
| 文件大小 | 280.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-18 00:00:00 | ||
图片预览

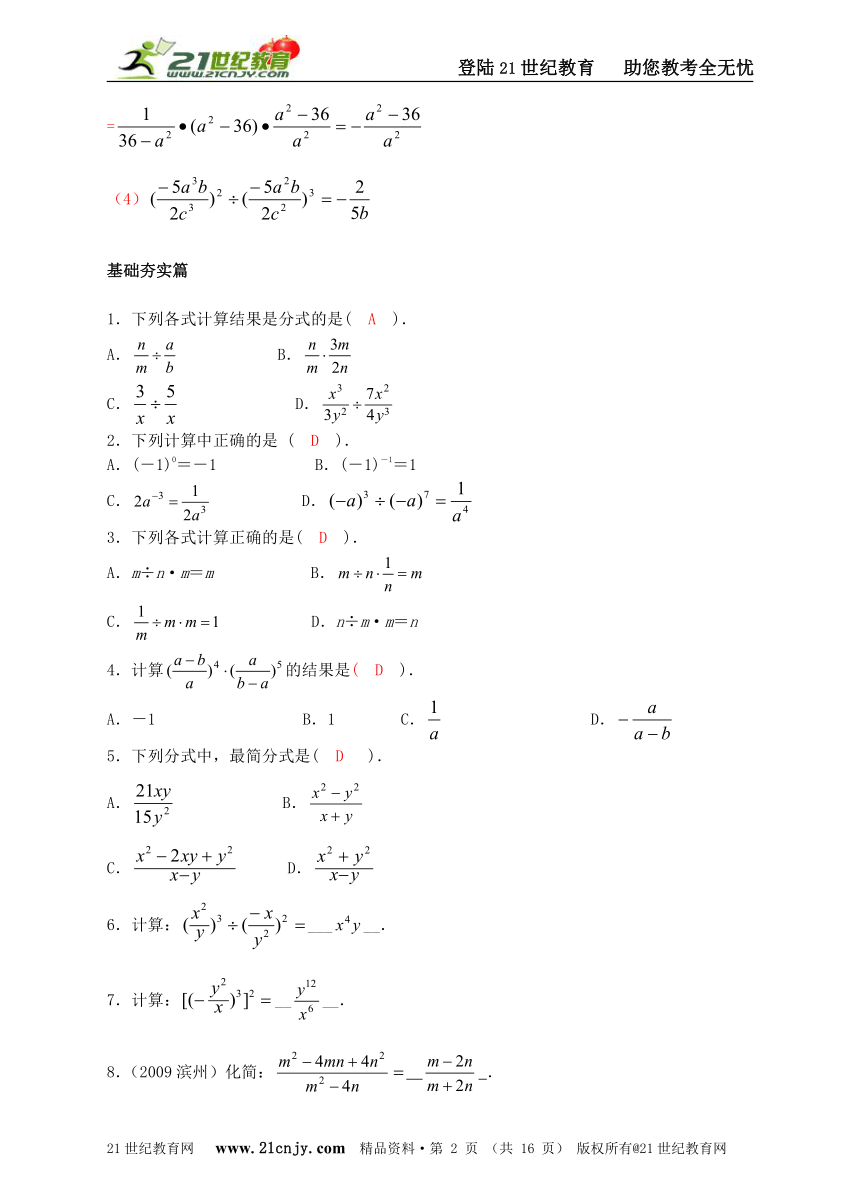



文档简介
登陆21世纪教育 助您教考全无忧
第十六章 分式
16.2 分式的运算
第1课时(共4课时)
课前预习篇
1.乘法法则:分式乘分式, 用分子的积作为积的分子,分母的积作为积的分母 .用式子表示为
2.除法法则:分式除以分式, 先把除式变为倒数,再与被除式相乘.用式子表示为
3.分式的乘方: 把分子分母分别乘方 .用式子表示为:.
4.注意:分子分母是多项式时,先分解因式便于约分.运算结果要化为最简分式.
典例剖析篇
【例1】计算:
(1) (2)
(3)
(4)
【解析】(1)分式的乘法,先将各个分式的分子、分母因式分解,然后约分.(2)分式的除法,常常转化为分式的乘法,再化简.(4)分式乘除法混合运算,没有括号的,要从左到右依次计算.(4)分式的乘方要注意分子,分母各项都需要乘方,特别是注意系数也要乘方.同时要注意符号的变化.
解:(1)=
(2)
(3)
=
(4)
基础夯实篇
1.下列各式计算结果是分式的是( A ).
A. B.
C. D.
2.下列计算中正确的是 ( D ).
A.(-1)0=-1 B.(-1)-1=1
C. D.
3.下列各式计算正确的是( D ).
A.m÷n·m=m B.
C. D.n÷m·m=n
4.计算的结果是( D ).
A.-1 B.1 C. D.
5.下列分式中,最简分式是( D ).
A. B.
C. D.
6.计算:_____.
7.计算:____.
8.(2009滨州)化简: .
9.计算:(1)
(2)
解(1):原式=
=
(2)原式==
决胜中考篇
10.(2010连云港)化简:(a-2)·=_______.
11. (2010滨州)化简: =_____.
12.(2009青岛)化简:;
解:原式
13.(2009长春)先化简,再求值:,其中.
解:原式=
当x=2时,原式==
14.(2009西宁)请从下列三个代数式中任选两个(一个作为分子,一个作为分母)构造一个分式,并化简该分式.
然后请你自选一个合理的数代入求值.
解:选择作分子,作分母,得分式,化简得:==
取a=2,代入得:=
15.(2010荆门)观察下列计算:
… …
从计算结果中找规律,利用规律性计算
=_____.
16. 已知,求的值.
解:因为,
所以设=k,则
.
将代入中,得:
原式=
第2课时(共4课时)
课前预习篇
1.分式的加减法法则是:同分母分式相相加减 分母不变,分子相加减 ,用式子表示为:异分母分式相加减 先通分,变为同分母的分式,再加减 .用式子表示为:.
2.分式混合运算的顺序与分数相同:即 先乘方,再乘除,然后加减 .
典例剖析篇
【例1】计算:(1)
(2)
【解析】同分母的分式相加减,分母不变,分子相加减;对于异分母的分式相加减,先通分,再加减.
解:(1)=
(2)=
【例2】(2010红河自治州)先化简再求值:选一个使原代数式有意义的数带入求值.
【解析】这是一道分式的混合运算题,对于分式混合运算要按先乘除后加减的顺序进行化简计算,最后代入使原分式有意义的a值,求值.
解:原式=
=
= =
当a=1时,原式=(a 的值不唯一,只要a不取2,-3即可)
基础夯实篇
1.下列运算中,计算正确的是( D ).
A. B.
C. D.
2.的结果是 ( C ).
A. B. C. D.
3.化简的结果是( B ).
A. B. C.x-y D.y-x
4. (2010黄冈) 化简:的结果是( B )
A.2 B. C. D.
5.(2009陕西)化简的结果是( B )
A. B. C. D.
6.(2009黄冈)化简的结果是( A )
A.-4 B.4 C.2a D.-2a
7.(2009威海)化简的结果是(D)
A. B. C. D.
8.(2009佳木斯)计算 HYPERLINK "http://www./" EMBED Equation.DSMT4 =
9.若实数满足则的最大值是 2 .
10. (2010黄冈)已知: 则式子 -6 .
11.(2009烟台市)设,,则的值等于 .
11.(2010无锡)计算:
解:原式=
==1
12.(2010镇江)计算化简
原式
13.(2010重庆潼南)先化简,再求值:÷ HYPERLINK "http://www./" EMBED Equation.3 EMBED Equation.3 ,其中x=2.
解:原式==.
当x=2时, 原式==.
决胜中考篇
14.(2009枣庄)a、b为实数,且ab=1,设 +,,则P = Q(填“>”、“<”或“=”).
15.(桂林2010)先化简,再求值: ÷,其中.
= ==
当时,原式
=
16.(2010镇江)描述证明:海宝在研究数学问题时发现一个有趣的现象:
(1)请你用数学表达式补充完整海宝发现的这个有趣的现象;
(2)请你证明海宝发现的这个有趣现象.
解:(1)
(2)证明:
所以
第3课时(共4课时)
课前预习篇
1. 通过以往的学习,我们知道,当m,n是正整数时,
对于,当m为负整数时,负整指数幂它又有怎样的性质呢?先看下列计算:;由此不难推出:是的倒数,即:
2.以前我们学过,一些较大的数,用科学记数法表示比较方便,例如:光速为3×m/s,那么,比较小的数,如细胞的直径等,能否用拉学记数法表示呢?学习了负整数指数幂后,这个问题就解决了.即小于1的正数可以用科学记数法表示为的形式,其中,a是整数数位只有一位的正数,n是正整数,如:0.000 000 005 3= .
典例剖析篇
【例1】 计算:
(1) (2);
(3)
【解析】对于正整数指数幂所适用的法则和运算律,负指数幂同样适用.
解:(1)=
(2)=
(3)==
【例2】用科学记数法表示0.000 000 92是 ;3.28×用小数表示为 .
【解析】用科学记数法表示数,一般写成a×10n的形式( 1≤|a|<10,n为整数),|n|就是小数点移到有且只有一位整数时的移动位数.
【答案】9.2× 0.000 328
基础演练篇
1.下列计算中,正确的是( D )
A.a2n÷a2n=a B.(a3-b3)÷(a-b)= a2-b2
C.a8n÷a2n=a4n D.(-a)10m÷(-a)5m=a5m(m为整数)
2.要使 有意义,那么x的范围是( D )
A.x>2 B.x<-2
C.x≠±2 D.x≠2且x≠-2
3.(2009佛山)下列关于数与式的等式中,正确的是( A )
A. B.
C. D.
4.计算的结果是( D )
A.1 B. C. D.
5.已知,则在中,最大的数是( D )
A. B. C. D.
6.(10湖南怀化)若,则、、的大小关系是( C )
A. B. C. D.
7.(2010南通)用科学记数法表示0.000031,结果是( B )
A.3.1×10-4 B.3.1×10-5 C.0.31×10-4 D.31×10-6
8.(2010宁波)据《中国经济周刊》报道,上海世博会第四轮环保活动投资总金额高达820亿元,其中820亿用科学记数法表示为( B )
A. B. C. D.
9. 某禽流感病毒直径为90 nm,则90 nm用科学记数法表示为( B )m.
A. B. C. D.
10.国际上对相对原子质量的规定是:相对原子质量是指元素的平均原子质量与碳-12原子质量的1/12之比.已知一氢原子的质量是,氢原子的相对原子质量为( C )
A.10 B.12 C.1 D.0.1
11.计算:(x-3y-2)2·(-x2y-2)-3= ;
(-2a2b2)5÷(-4ab4)2= ;
xy2 ·xy-4·2xm= 2xm+1y-2..
12.用科学记数法表示下列的数(保留3位有效数字):
5310= ;-534500000= ;
0.000003257= .
决胜中考篇
13.(2010黄冈)已知,则式子= -6 .
14.计算:
(1)(2010上海)
(2)(2010重庆)(-1)2010-| -7 |+ ×(-π)0+()-1
(3)(2010昆明)
解:(1)原式
(2)解:原式=1-7+3×1+5
=2
(3)解:原式=-4-3-1+2= -6
15.一种球状细菌的直径约是300 nm,体积约是.假如在一个容积为27 的容器内全部充满该细菌,则该容器内细菌的个数大约有多少?
解:27×÷()=
16.先化简再求值:,其中.
解:原式.
当=1时,原式.
17.水滴石穿是一个漫长的过程.水珠不断滴在一块石头上,经过10年,石头上形成了一个深为的小洞.假设每月小洞增加的深度相同,石头的厚度为0.3 m ,则再经过多少年,可以达到水滴石穿?
解:(30-5)÷=50
第4课时(共4课时)
课前预习篇
1.本节主要学习了分式的乘除、分式的加减及负整数指数幂等相关内容.
2.分式的混合运算:在分式的混合运算中,应先算乘方,再将除法化为乘法,进行约分化简,最后进行加减运算.如果有括号,要先算括号里面的.注意:运算的结果必须是最简分式或整式.
典例剖析篇
【例1】(2010德州)先化简,再求值:,其中.
【解析】此类题不可直接代值求解,需先将式子化成最简分式或整式,再代值求解.化简时,要按运算顺序进得,在分式的约分化简过程中,分子分母能分解因式的要考虑先分解因式,这样计算才能更简便.
解:原式=
=
==.
当时,原式=.
【例2】先化简,再求值:,其中a满足.
【解析】根据已知条件,在计算时要把看成一个整体,这样问题就相对容易得多.在数学学习中,整体思想的运用常常能达到事半功倍的效果.
解:原式===
当a满足时,,
所以原式=1
基础夯实篇
1.(2010黄冈)化简:的结果是( B )
A.2 B. C. D.
2.(2009黄冈)化简 的结果是( A )
A.-4 B.4 C.2a D.-2a0
3.(2009包头)化简, 其结果是( D )
A. B. C. D.
4.(2010怀化)若0<<1,则、、的大小关系是( C )
A.<< B. <<
C. << D. <<
5.(2010凉山)已知:与 || 互为相数,则式子的值等于 .
6.先化简,再计算:(1+)÷,其中a=-3.
解:原式=(+)×
=× =a+2
把a=-3代入得,原式=-3+2=-1
决胜中考篇
7. (2010凉山)若,则 .
8.(2010肇庆)先化简,后求值:,其中.
解:
=
=
=
当时,原式==.
9.先化简代数式÷,然后选取一个合适的a值,代入求值.
解: 方法一: 原式=
=
=
方法二:原式=
==
取a=1,得原式=5
10.(2010娄底)已知:
.试说明不论x为任何有意义的值,y的值均不变.
解:
所以无论 x取何值,y的值均会变.
11.(2010甘肃)观察:,,…,则
(n=1,2,3,…).
12.(2010贵阳)先化简:,当时,再从-2<<2的范围内选取一个合适的整数代入求值.
解:原式=
在-2<<2中,a可取的整数为-1、0、1,而当b=-1时,
①若a=-1,分式无意义;
②若a=0,分式无意义;
③若a=1,分式无意义.
所以a在规定的范围内取整数,原式均无意义(或所求值不存在)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 16 页) 版权所有@21世纪教育网
第十六章 分式
16.2 分式的运算
第1课时(共4课时)
课前预习篇
1.乘法法则:分式乘分式, 用分子的积作为积的分子,分母的积作为积的分母 .用式子表示为
2.除法法则:分式除以分式, 先把除式变为倒数,再与被除式相乘.用式子表示为
3.分式的乘方: 把分子分母分别乘方 .用式子表示为:.
4.注意:分子分母是多项式时,先分解因式便于约分.运算结果要化为最简分式.
典例剖析篇
【例1】计算:
(1) (2)
(3)
(4)
【解析】(1)分式的乘法,先将各个分式的分子、分母因式分解,然后约分.(2)分式的除法,常常转化为分式的乘法,再化简.(4)分式乘除法混合运算,没有括号的,要从左到右依次计算.(4)分式的乘方要注意分子,分母各项都需要乘方,特别是注意系数也要乘方.同时要注意符号的变化.
解:(1)=
(2)
(3)
=
(4)
基础夯实篇
1.下列各式计算结果是分式的是( A ).
A. B.
C. D.
2.下列计算中正确的是 ( D ).
A.(-1)0=-1 B.(-1)-1=1
C. D.
3.下列各式计算正确的是( D ).
A.m÷n·m=m B.
C. D.n÷m·m=n
4.计算的结果是( D ).
A.-1 B.1 C. D.
5.下列分式中,最简分式是( D ).
A. B.
C. D.
6.计算:_____.
7.计算:____.
8.(2009滨州)化简: .
9.计算:(1)
(2)
解(1):原式=
=
(2)原式==
决胜中考篇
10.(2010连云港)化简:(a-2)·=_______.
11. (2010滨州)化简: =_____.
12.(2009青岛)化简:;
解:原式
13.(2009长春)先化简,再求值:,其中.
解:原式=
当x=2时,原式==
14.(2009西宁)请从下列三个代数式中任选两个(一个作为分子,一个作为分母)构造一个分式,并化简该分式.
然后请你自选一个合理的数代入求值.
解:选择作分子,作分母,得分式,化简得:==
取a=2,代入得:=
15.(2010荆门)观察下列计算:
… …
从计算结果中找规律,利用规律性计算
=_____.
16. 已知,求的值.
解:因为,
所以设=k,则
.
将代入中,得:
原式=
第2课时(共4课时)
课前预习篇
1.分式的加减法法则是:同分母分式相相加减 分母不变,分子相加减 ,用式子表示为:异分母分式相加减 先通分,变为同分母的分式,再加减 .用式子表示为:.
2.分式混合运算的顺序与分数相同:即 先乘方,再乘除,然后加减 .
典例剖析篇
【例1】计算:(1)
(2)
【解析】同分母的分式相加减,分母不变,分子相加减;对于异分母的分式相加减,先通分,再加减.
解:(1)=
(2)=
【例2】(2010红河自治州)先化简再求值:选一个使原代数式有意义的数带入求值.
【解析】这是一道分式的混合运算题,对于分式混合运算要按先乘除后加减的顺序进行化简计算,最后代入使原分式有意义的a值,求值.
解:原式=
=
= =
当a=1时,原式=(a 的值不唯一,只要a不取2,-3即可)
基础夯实篇
1.下列运算中,计算正确的是( D ).
A. B.
C. D.
2.的结果是 ( C ).
A. B. C. D.
3.化简的结果是( B ).
A. B. C.x-y D.y-x
4. (2010黄冈) 化简:的结果是( B )
A.2 B. C. D.
5.(2009陕西)化简的结果是( B )
A. B. C. D.
6.(2009黄冈)化简的结果是( A )
A.-4 B.4 C.2a D.-2a
7.(2009威海)化简的结果是(D)
A. B. C. D.
8.(2009佳木斯)计算 HYPERLINK "http://www./" EMBED Equation.DSMT4 =
9.若实数满足则的最大值是 2 .
10. (2010黄冈)已知: 则式子 -6 .
11.(2009烟台市)设,,则的值等于 .
11.(2010无锡)计算:
解:原式=
==1
12.(2010镇江)计算化简
原式
13.(2010重庆潼南)先化简,再求值:÷ HYPERLINK "http://www./" EMBED Equation.3 EMBED Equation.3 ,其中x=2.
解:原式==.
当x=2时, 原式==.
决胜中考篇
14.(2009枣庄)a、b为实数,且ab=1,设 +,,则P = Q(填“>”、“<”或“=”).
15.(桂林2010)先化简,再求值: ÷,其中.
= ==
当时,原式
=
16.(2010镇江)描述证明:海宝在研究数学问题时发现一个有趣的现象:
(1)请你用数学表达式补充完整海宝发现的这个有趣的现象;
(2)请你证明海宝发现的这个有趣现象.
解:(1)
(2)证明:
所以
第3课时(共4课时)
课前预习篇
1. 通过以往的学习,我们知道,当m,n是正整数时,
对于,当m为负整数时,负整指数幂它又有怎样的性质呢?先看下列计算:;由此不难推出:是的倒数,即:
2.以前我们学过,一些较大的数,用科学记数法表示比较方便,例如:光速为3×m/s,那么,比较小的数,如细胞的直径等,能否用拉学记数法表示呢?学习了负整数指数幂后,这个问题就解决了.即小于1的正数可以用科学记数法表示为的形式,其中,a是整数数位只有一位的正数,n是正整数,如:0.000 000 005 3= .
典例剖析篇
【例1】 计算:
(1) (2);
(3)
【解析】对于正整数指数幂所适用的法则和运算律,负指数幂同样适用.
解:(1)=
(2)=
(3)==
【例2】用科学记数法表示0.000 000 92是 ;3.28×用小数表示为 .
【解析】用科学记数法表示数,一般写成a×10n的形式( 1≤|a|<10,n为整数),|n|就是小数点移到有且只有一位整数时的移动位数.
【答案】9.2× 0.000 328
基础演练篇
1.下列计算中,正确的是( D )
A.a2n÷a2n=a B.(a3-b3)÷(a-b)= a2-b2
C.a8n÷a2n=a4n D.(-a)10m÷(-a)5m=a5m(m为整数)
2.要使 有意义,那么x的范围是( D )
A.x>2 B.x<-2
C.x≠±2 D.x≠2且x≠-2
3.(2009佛山)下列关于数与式的等式中,正确的是( A )
A. B.
C. D.
4.计算的结果是( D )
A.1 B. C. D.
5.已知,则在中,最大的数是( D )
A. B. C. D.
6.(10湖南怀化)若,则、、的大小关系是( C )
A. B. C. D.
7.(2010南通)用科学记数法表示0.000031,结果是( B )
A.3.1×10-4 B.3.1×10-5 C.0.31×10-4 D.31×10-6
8.(2010宁波)据《中国经济周刊》报道,上海世博会第四轮环保活动投资总金额高达820亿元,其中820亿用科学记数法表示为( B )
A. B. C. D.
9. 某禽流感病毒直径为90 nm,则90 nm用科学记数法表示为( B )m.
A. B. C. D.
10.国际上对相对原子质量的规定是:相对原子质量是指元素的平均原子质量与碳-12原子质量的1/12之比.已知一氢原子的质量是,氢原子的相对原子质量为( C )
A.10 B.12 C.1 D.0.1
11.计算:(x-3y-2)2·(-x2y-2)-3= ;
(-2a2b2)5÷(-4ab4)2= ;
xy2 ·xy-4·2xm= 2xm+1y-2..
12.用科学记数法表示下列的数(保留3位有效数字):
5310= ;-534500000= ;
0.000003257= .
决胜中考篇
13.(2010黄冈)已知,则式子= -6 .
14.计算:
(1)(2010上海)
(2)(2010重庆)(-1)2010-| -7 |+ ×(-π)0+()-1
(3)(2010昆明)
解:(1)原式
(2)解:原式=1-7+3×1+5
=2
(3)解:原式=-4-3-1+2= -6
15.一种球状细菌的直径约是300 nm,体积约是.假如在一个容积为27 的容器内全部充满该细菌,则该容器内细菌的个数大约有多少?
解:27×÷()=
16.先化简再求值:,其中.
解:原式.
当=1时,原式.
17.水滴石穿是一个漫长的过程.水珠不断滴在一块石头上,经过10年,石头上形成了一个深为的小洞.假设每月小洞增加的深度相同,石头的厚度为0.3 m ,则再经过多少年,可以达到水滴石穿?
解:(30-5)÷=50
第4课时(共4课时)
课前预习篇
1.本节主要学习了分式的乘除、分式的加减及负整数指数幂等相关内容.
2.分式的混合运算:在分式的混合运算中,应先算乘方,再将除法化为乘法,进行约分化简,最后进行加减运算.如果有括号,要先算括号里面的.注意:运算的结果必须是最简分式或整式.
典例剖析篇
【例1】(2010德州)先化简,再求值:,其中.
【解析】此类题不可直接代值求解,需先将式子化成最简分式或整式,再代值求解.化简时,要按运算顺序进得,在分式的约分化简过程中,分子分母能分解因式的要考虑先分解因式,这样计算才能更简便.
解:原式=
=
==.
当时,原式=.
【例2】先化简,再求值:,其中a满足.
【解析】根据已知条件,在计算时要把看成一个整体,这样问题就相对容易得多.在数学学习中,整体思想的运用常常能达到事半功倍的效果.
解:原式===
当a满足时,,
所以原式=1
基础夯实篇
1.(2010黄冈)化简:的结果是( B )
A.2 B. C. D.
2.(2009黄冈)化简 的结果是( A )
A.-4 B.4 C.2a D.-2a0
3.(2009包头)化简, 其结果是( D )
A. B. C. D.
4.(2010怀化)若0<<1,则、、的大小关系是( C )
A.<< B. <<
C. << D. <<
5.(2010凉山)已知:与 || 互为相数,则式子的值等于 .
6.先化简,再计算:(1+)÷,其中a=-3.
解:原式=(+)×
=× =a+2
把a=-3代入得,原式=-3+2=-1
决胜中考篇
7. (2010凉山)若,则 .
8.(2010肇庆)先化简,后求值:,其中.
解:
=
=
=
当时,原式==.
9.先化简代数式÷,然后选取一个合适的a值,代入求值.
解: 方法一: 原式=
=
=
方法二:原式=
==
取a=1,得原式=5
10.(2010娄底)已知:
.试说明不论x为任何有意义的值,y的值均不变.
解:
所以无论 x取何值,y的值均会变.
11.(2010甘肃)观察:,,…,则
(n=1,2,3,…).
12.(2010贵阳)先化简:,当时,再从-2<<2的范围内选取一个合适的整数代入求值.
解:原式=
在-2<<2中,a可取的整数为-1、0、1,而当b=-1时,
①若a=-1,分式无意义;
②若a=0,分式无意义;
③若a=1,分式无意义.
所以a在规定的范围内取整数,原式均无意义(或所求值不存在)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 16 页) 版权所有@21世纪教育网
