人教版数学八年级下册第18章18.1勾股定理课时同步训练
文档属性
| 名称 | 人教版数学八年级下册第18章18.1勾股定理课时同步训练 |

|
|
| 格式 | rar | ||
| 文件大小 | 392.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-18 00:00:00 | ||
图片预览



文档简介
登陆21世纪教育 助您教考全无忧
第十八章 勾股定理
18.1勾股定理
第1课时(共3课时)
课前预习篇
1. 勾股定理:如果直角三角形的两直角边分别是a、b,斜边为c,那么a2+b2=___c2_____.例如:如果直角三角形的两直角边分别是1、1,则斜边为________.
2. 勾股定理的证明:勾股定理常用面积相等的方法进证明.
3. 勾股定理的适用范围:勾股定理存在于直角三角形中,不是直角三角形就不能直接使用勾股定理.
典例剖析篇
考点1.勾股定理的证明
【例1】已知:如图,边长为(a+b)的大正方形被分为4个全等的直角边为a,b,斜边为c的直角三角形和一个边长为c的正方形.
求证:a2+b2=c2.
【解析】证明勾股定理的方法有300多种,此题是其中的一种证明方法.利用面积相等可以得出证明.
证明:大正方形的面积为:
大正方形的面积还可以表示为:
=
所以=.
所以=
考点2.利用勾股定理进行计算
【例2】如图,在△ABC中,AD是BC边上的高,且AD=12,AB=13,BC=14.求AC的长.
【解析】由勾股定理先求BD 、CD,再求AC.
解:因为CD为高,
所以△ACD和△ABD为直角三角形
所以由勾股定理得:BD2=AB2-AD2=132-122=25,即BD=5,
所以CD=BC-BD=14-5=9.
在Rt△ACD中,因为AD=12,CD=9,所以=
所以
基础夯实篇
3.在Rt△ABC中,∠C=90°,a=12,b=16,则c的长为( C )
A.26 B.18 C.20 D.21
4.一直角三角形的三边分别为2、3、x,那么以x为边长的正方形的面积为( C )
A.13 B.5 C.13或5 D.无法确定
5.将一个直角三角形两直角边同时扩大到原来的两倍,则斜边扩大到原来的( B )
A.4倍 B.2倍 C.不变 D.无法确定
6.正方形的面积是4,则它的对角线长是( C )
A.2 B. C. D.4
7.如图,在△ABC中,AD⊥BC于D,AB=3,BD=2,DC=1,则AC=( B )
A.6
B.
C.
D.4
8.如图:a,b,c表示以直角三角形三边为边长的正方形的面积,则下列结论正确的是( C )
A. a2 + b2=c2
B. ab=c
C. a+b=c
D. a+ b=c2
9.写出一组是3个连续偶数的勾股数: 6,8,10 ;
写出一组是3个连续自然数的勾股数: 3,4,5 .
10.一个三角形的三个内角∠A:∠B:∠C=1:2:3,则此三角形是___直角____三角形;若此三角形的三边对应分别为a、b、c,则此三角形的三边的关系是___ a2+b2= c2_______.
11.△ABC的三边a、b、c,若满足b2= a2+c2,则 ∠C =90°; 若满足b2>c2+a2,则∠B是 钝 角; 若满足b2<c2+a2,则∠B是 锐 角.
12.若直角三角形的边长为6,8,则第三边长为 10或2 .
13.在Rt△ABC中,∠B=60°,∠C=90°,AB=10,则BC= 5 ,AC= .
决胜中考篇
14.(2010眉山)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( C )
A.90°
B.60°
C.45°
D.30°
15.(2009年长沙)如图,等腰三角形ABC中,AB=AC,AD是底边上的高,若,则 4 cm.
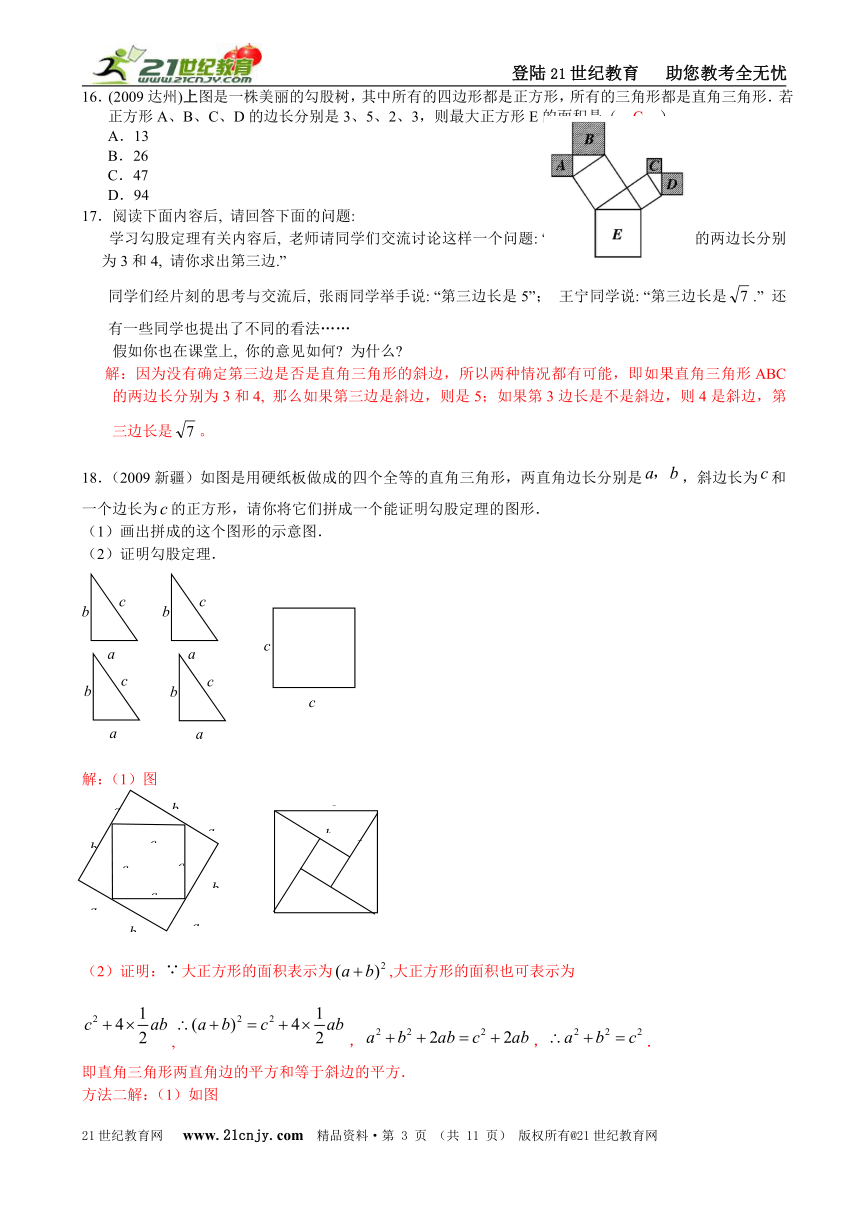
16.(2009达州)上图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( C )
A.13
B.26
C.47
D.94
17.阅读下面内容后, 请回答下面的问题:
学习勾股定理有关内容后, 老师请同学们交流讨论这样一个问题: “已知直角三角形ABC的两边长分别为3和4, 请你求出第三边.”
同学们经片刻的思考与交流后, 张雨同学举手说: “第三边长是5”; 王宁同学说: “第三边长是.” 还有一些同学也提出了不同的看法……
假如你也在课堂上, 你的意见如何 为什么
解:因为没有确定第三边是否是直角三角形的斜边,所以两种情况都有可能,即如果直角三角形ABC的两边长分别为3和4, 那么如果第三边是斜边,则是5;如果第3边长是不是斜边,则4是斜边,第三边长是。
18.(2009新疆)如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别是,斜边长为和一个边长为的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图.
(2)证明勾股定理.
解:(1)图
(2)证明:大正方形的面积表示为,大正方形的面积也可表示为
,,,.
即直角三角形两直角边的平方和等于斜边的平方.
方法二解:(1)如图
(2)证明:大正方形的面积表示为:,又可以表示为:,,,.即直角三角形两直角边的平方和等于斜边的平方.
第2课时(共3课时)
课前预习篇
1. 勾股定理的应用:
①已知直角三角形的两边,求第三边;②已知直角三角形的一边,求另两边的关系;
③用于证明有关线段平方关系的问题
2. 当多边形中不能直接应用勾股定理时,适当添加辅助线将其转化为直角三角形问题来解决.
3.理解勾股定理的一些变式 :c2=a2+b2, a2=c2-b2,b2=c2-a2 c2=(a+b)2-2ab, 2ab=(a+b+c)(a+b-c)
典例剖析篇
【例1】如图3,已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
解:根据题意得:Rt△ADE≌Rt△AEF
所以∠AFE=90°,AF=10 cm,EF=DE
设CE=x cm,则DE=EF=CD-CE=8-x
在Rt△ABF中由勾股定理得:
AB2+BF2=AF2,即82+BF2=102,
所以BF=6 cm
所以CF=BC-BF=10-6=4(cm)
在Rt△ECF中由勾股定理可得:
EF2=CE2+CF2,即(8-x)2=x2+42
所以64-16x+x2=x2+16
所以x=3(cm),即CE=3 cm.
【例2】已知:如图,在△ABC中,∠ACB=90°,D为AC上任意一点.求证:
【解析】在直角三角形中,如果有证明有关线段平方关系的问题,用勾股定理的思想来解决.
证明:在Rt△DBC中,因为∠ACB=90°,所以由勾股定理可得:.
在Rt △ABC中,∠ACB=90°,
所以,
所以
所以.
基础夯实篇
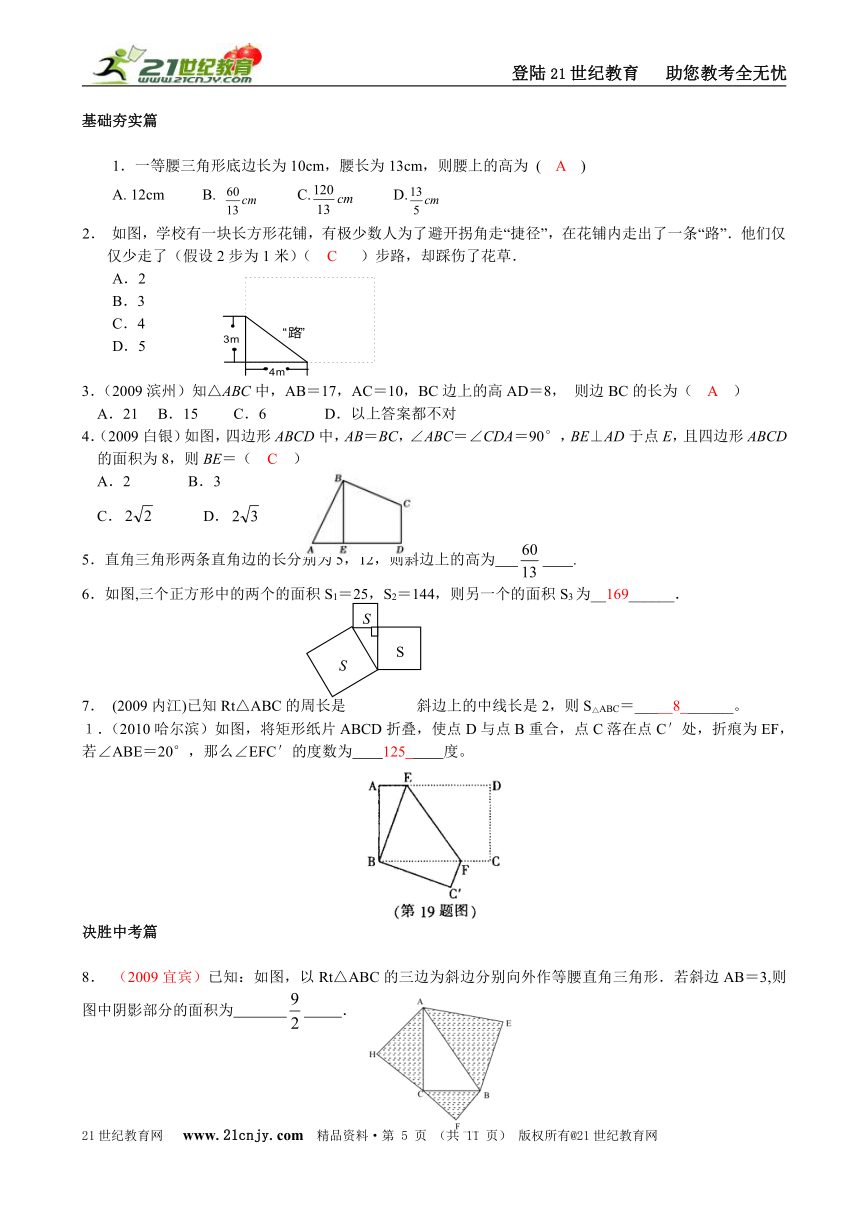
1.一等腰三角形底边长为10cm,腰长为13cm,则腰上的高为 ( A )
A. 12cm B. C. D.
2. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了(假设2步为1米)( C )步路,却踩伤了花草.
A.2
B.3
C.4
D.5
3.(2009滨州)知△ABC中,AB=17,AC=10,BC边上的高AD=8, 则边BC的长为( A )
A.21 B.15 C.6 D.以上答案都不对
4.(2009白银)如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( C )
A.2 B.3
C. D.
5.直角三角形两条直角边的长分别为5,12,则斜边上的高为 .
6.如图,三个正方形中的两个的面积S1=25,S2=144,则另一个的面积S3为__169______.
7. (2009内江)已知Rt△ABC的周长是,斜边上的中线长是2,则S△ABC=_____8_______。
1.(2010哈尔滨)如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为 125 度。
决胜中考篇
8. (2009宜宾)已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为 .
10.(2009临沂)如图,过原点的直线l与反比例函数的图像交于M,N两点,根据图像猜想线段MN的长的最小值是___________.
11.如下表,表中所给的每行的三个数a、b、c,有a<b<c,试根据表中已有数的规律,写出当a=27时,b,c的值,并把b、c用含a的代数式表示出来.
3,4,5 32+42=52
5,12,13 52+122=132
7,24,25 72+242=252
9,40,41 92+402=412
...... ……
27,b,c 272+b2=c2
解:当a=27时,b=364,c=365
,
12.如图,一架长5m的梯子AB,斜立在一竖直的墙上,这时梯子底端距墙底3m.如果梯子的顶端沿墙下滑1m,梯子的底端的水平方向沿一条直线也将滑动1m吗?如果梯子顶端下滑2 m呢?用所学知识,论证你的结论.
解:当梯子顶端下滑1米时,
如图,在Rt△ABC中,∠C=90°,
AB=5,BC=3,
所以由勾股定理得:
AC==4
梯子下滑后,如图,在Rt△DCE中,DE=5,DC=AC-1=3,
所以CE==4
所以梯子顶端下滑1m时,底端移动的距离为CE-BC=4-3=1 m.若梯子顶端下滑2 m,则AD=2,DC=4-2=2,此时
CE=
此时梯子滑动的距离为CE-BC=-3
12.(2009定西)如图13,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点。
求证:(1);
(2).
证明:(1) 因为∠ACB=∠ECD,
所以∠ACD+∠BCD=∠ACD+∠ACE.
即∠BCD=∠ACE.
因为BC=AC,DC=EC, 所以 △ACE≌△BCD.
(2)因为△ACB是等腰直角三角形,
所以∠B=∠BAC=45°.
因为 △ACE≌△BCD, 所以∠B=∠CAE=45°.
所以∠DAE=∠CAE+∠BAC= 45°+45°=90°.
所以.
由(1)知AE=DB,所以.
10.有一根70cm长的木棒,要放在长、宽、高分别是40cm、30cm、50cm的木盒中,能放进去吗?通过计算说明理由.
解:能放进去.
木盒中能放的最长的木棒的长度是DB′的长度.
在Rt△BDC中,BD= =
在Rt△BDB′中,由勾股定理得:B′D= = >70,
所以能放进去.
第3课时(共3课时)
课前预习篇
1.勾股定理在实际生活中应用非常广泛,要善于把实际问题转化为数学问题,特别是能准确的画出图形
2.数轴上的点不但可以表示__有理____数,也可以表示__无理____数,实数与数轴上的点是__一一对应______的.
典例剖析篇
【例1】如图,网格中的每个小正方形边长都是1,请在图中画出表示,这样的线段.
解:如图,AB、CD、EF,GH分别表示,.
【例2】台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市A的正南方向240千米B处有一台风中心,其中心最大风力为12级,每远离台风中心25千米,风力就会减弱一级,该台风中心现正以20千米/时的速度沿北偏东30°方向往C移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响.
(1)该城市是否会受到这次台风的影响?请说明理由.
(2)若会受到观风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受台风影响的最大风力为几级?
【解析】将实际问题转化为数学问题,利用勾股定理求解.
解:(1)作AH⊥BC于H
在Rt△ABH中,因为∠B=30°,
所以(千米)
又因为台风中心的影响半径为(12-4)×25=200(千米)
所以城市A要受台风影响.
(2)假设台风从M处开始影响A市,到N处结束,连接AM、AN.
在Rt△AMH中,
因为MH2=AM2-AH2=25600
所以MH=160(千米)
所以台风影响该城市的持续时间为(2×160)÷20=16(小时)
(3)该城市受台风影响的最大风力为12-120÷25=7.2(级)
基础夯实篇
1.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( C )
A.0
B.1
C.2
D.3
2.在测量旗杆的方案中,若旗杆高为21m,目测点到杆的距离为15m,则目测点到杆顶的距离为(设目高为1m) ( B )
A.20m B.25m C.30m D.35m
3.(2009恩施)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( B )
A. B.25 C. D.
4.木工师傅要做一个长方形桌面,做好后量得长为80cm,宽为60cm,对角线为100cm,则这个桌面 合格 .(填“合格”或“不合格” )
5.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了520m,求该河流的宽度为___480 m ______.
6.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高___15___米.
7.(2010德州)如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为__ 4___m.
决胜中考篇
8.(2009滨州)某楼梯的侧面视图如图4所示,其中AB=4 m,,,因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的长度应为 (2+2)米 .
9.(2009年安徽)13、长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了 m.
10.(2009安顺)图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是___76 .
11.(2010厦门)如图3,以第①个等腰直角三角形的斜边长作为第②个等腰直角三角形的腰,以第②个等腰直角三角形的斜边长做为第③个等腰直角三角形的腰,依次类推,若第⑨个等腰直角三角形的斜边长为厘米,则第①个等腰直角三角形的斜边长为 ______厘米.
12.在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中按下列要求画出图形.
(1)从点A出发画一条线段AB,使它的另一端点B在格点上,且长度为;
(2)画出所有的以(1)中的AB为边的等腰三角形,使另一个顶点在格点上,且令两边的长度都是无理数.
12.如图,某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点处有人求救,便立即派三名救生员前去营救.1号救生员从A点直接跳入海中;2号救生员沿岸边(岸边看成是直线)向前跑50米到C点,再跳入海中;3号救生员沿岸边向前跑200米到离B点最近的D点,再跳入海中.若三名救生员同时从A点出发,他们在岸边跑的速度都是5米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°,请你通过计算说明谁先到达营救地点B.
.解:在△ABD中,∠BAD=45°,, .
所以∠ABD=45°,BD=AD=200,
所以由勾股定理得:.
在中,,所以.
所以1号救生员到达B点所用的时间为(秒)
2号救生员到达B点所用的时间为(秒),
3号救生员到达B点所用的时间为(秒).
,所以2号救生员先到达营救地点.
13.中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?
解:在Rt△ABC中, BC2=AB2-AC2=502-302=1600,
所以BC=40
所以汽车的行驶速度为40÷2=20(m/s)=72(km/h)
因为72>70 所以小汽车超速了
答:这辆小汽车超速了.
14.(2009牡丹江)有一块直角三角形的绿地,量得两直角边长分别为现在要将绿地扩充成等腰三角形,且扩充部分是以为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
解:在Rt△ABC中,,由勾股定理有:,扩充部分为Rt△ABC,扩充成等腰△ABD.应分以下三种情况:①如图1,当AB=AD=10时,可求CD=CB=6,得△ABD的周长为32m.②如图2,当AB=BD=10时,可求CD=4,由勾股定理得:AD=4,得△ABD的周长为,③如图3,当AB为底时,设AD=BD=x,则CD=x-6,由勾股定理得:,得△ABD的周长为 m.
l
N
M
x
y
O
S3
S27S2
S11
c
b
a
a
a
a
b
b
b
c
c
c
c
b
a
c
c
a
b
c
a
b
c
a
b
c
a
b
c
B
D
C
A
c
b
5
20
15
10
C
A
B
A时
B时
B
C
A
30°
观测点
小汽车
小汽车
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 11 页) 版权所有@21世纪教育网
第十八章 勾股定理
18.1勾股定理
第1课时(共3课时)
课前预习篇
1. 勾股定理:如果直角三角形的两直角边分别是a、b,斜边为c,那么a2+b2=___c2_____.例如:如果直角三角形的两直角边分别是1、1,则斜边为________.
2. 勾股定理的证明:勾股定理常用面积相等的方法进证明.
3. 勾股定理的适用范围:勾股定理存在于直角三角形中,不是直角三角形就不能直接使用勾股定理.
典例剖析篇
考点1.勾股定理的证明
【例1】已知:如图,边长为(a+b)的大正方形被分为4个全等的直角边为a,b,斜边为c的直角三角形和一个边长为c的正方形.
求证:a2+b2=c2.
【解析】证明勾股定理的方法有300多种,此题是其中的一种证明方法.利用面积相等可以得出证明.
证明:大正方形的面积为:
大正方形的面积还可以表示为:
=
所以=.
所以=
考点2.利用勾股定理进行计算
【例2】如图,在△ABC中,AD是BC边上的高,且AD=12,AB=13,BC=14.求AC的长.
【解析】由勾股定理先求BD 、CD,再求AC.
解:因为CD为高,
所以△ACD和△ABD为直角三角形
所以由勾股定理得:BD2=AB2-AD2=132-122=25,即BD=5,
所以CD=BC-BD=14-5=9.
在Rt△ACD中,因为AD=12,CD=9,所以=
所以
基础夯实篇
3.在Rt△ABC中,∠C=90°,a=12,b=16,则c的长为( C )
A.26 B.18 C.20 D.21
4.一直角三角形的三边分别为2、3、x,那么以x为边长的正方形的面积为( C )
A.13 B.5 C.13或5 D.无法确定
5.将一个直角三角形两直角边同时扩大到原来的两倍,则斜边扩大到原来的( B )
A.4倍 B.2倍 C.不变 D.无法确定
6.正方形的面积是4,则它的对角线长是( C )
A.2 B. C. D.4
7.如图,在△ABC中,AD⊥BC于D,AB=3,BD=2,DC=1,则AC=( B )
A.6
B.
C.
D.4
8.如图:a,b,c表示以直角三角形三边为边长的正方形的面积,则下列结论正确的是( C )
A. a2 + b2=c2
B. ab=c
C. a+b=c
D. a+ b=c2
9.写出一组是3个连续偶数的勾股数: 6,8,10 ;
写出一组是3个连续自然数的勾股数: 3,4,5 .
10.一个三角形的三个内角∠A:∠B:∠C=1:2:3,则此三角形是___直角____三角形;若此三角形的三边对应分别为a、b、c,则此三角形的三边的关系是___ a2+b2= c2_______.
11.△ABC的三边a、b、c,若满足b2= a2+c2,则 ∠C =90°; 若满足b2>c2+a2,则∠B是 钝 角; 若满足b2<c2+a2,则∠B是 锐 角.
12.若直角三角形的边长为6,8,则第三边长为 10或2 .
13.在Rt△ABC中,∠B=60°,∠C=90°,AB=10,则BC= 5 ,AC= .
决胜中考篇
14.(2010眉山)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( C )
A.90°
B.60°
C.45°
D.30°
15.(2009年长沙)如图,等腰三角形ABC中,AB=AC,AD是底边上的高,若,则 4 cm.
16.(2009达州)上图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( C )
A.13
B.26
C.47
D.94
17.阅读下面内容后, 请回答下面的问题:
学习勾股定理有关内容后, 老师请同学们交流讨论这样一个问题: “已知直角三角形ABC的两边长分别为3和4, 请你求出第三边.”
同学们经片刻的思考与交流后, 张雨同学举手说: “第三边长是5”; 王宁同学说: “第三边长是.” 还有一些同学也提出了不同的看法……
假如你也在课堂上, 你的意见如何 为什么
解:因为没有确定第三边是否是直角三角形的斜边,所以两种情况都有可能,即如果直角三角形ABC的两边长分别为3和4, 那么如果第三边是斜边,则是5;如果第3边长是不是斜边,则4是斜边,第三边长是。
18.(2009新疆)如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别是,斜边长为和一个边长为的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图.
(2)证明勾股定理.
解:(1)图
(2)证明:大正方形的面积表示为,大正方形的面积也可表示为
,,,.
即直角三角形两直角边的平方和等于斜边的平方.
方法二解:(1)如图
(2)证明:大正方形的面积表示为:,又可以表示为:,,,.即直角三角形两直角边的平方和等于斜边的平方.
第2课时(共3课时)
课前预习篇
1. 勾股定理的应用:
①已知直角三角形的两边,求第三边;②已知直角三角形的一边,求另两边的关系;
③用于证明有关线段平方关系的问题
2. 当多边形中不能直接应用勾股定理时,适当添加辅助线将其转化为直角三角形问题来解决.
3.理解勾股定理的一些变式 :c2=a2+b2, a2=c2-b2,b2=c2-a2 c2=(a+b)2-2ab, 2ab=(a+b+c)(a+b-c)
典例剖析篇
【例1】如图3,已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
解:根据题意得:Rt△ADE≌Rt△AEF
所以∠AFE=90°,AF=10 cm,EF=DE
设CE=x cm,则DE=EF=CD-CE=8-x
在Rt△ABF中由勾股定理得:
AB2+BF2=AF2,即82+BF2=102,
所以BF=6 cm
所以CF=BC-BF=10-6=4(cm)
在Rt△ECF中由勾股定理可得:
EF2=CE2+CF2,即(8-x)2=x2+42
所以64-16x+x2=x2+16
所以x=3(cm),即CE=3 cm.
【例2】已知:如图,在△ABC中,∠ACB=90°,D为AC上任意一点.求证:
【解析】在直角三角形中,如果有证明有关线段平方关系的问题,用勾股定理的思想来解决.
证明:在Rt△DBC中,因为∠ACB=90°,所以由勾股定理可得:.
在Rt △ABC中,∠ACB=90°,
所以,
所以
所以.
基础夯实篇
1.一等腰三角形底边长为10cm,腰长为13cm,则腰上的高为 ( A )
A. 12cm B. C. D.
2. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了(假设2步为1米)( C )步路,却踩伤了花草.
A.2
B.3
C.4
D.5
3.(2009滨州)知△ABC中,AB=17,AC=10,BC边上的高AD=8, 则边BC的长为( A )
A.21 B.15 C.6 D.以上答案都不对
4.(2009白银)如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( C )
A.2 B.3
C. D.
5.直角三角形两条直角边的长分别为5,12,则斜边上的高为 .
6.如图,三个正方形中的两个的面积S1=25,S2=144,则另一个的面积S3为__169______.
7. (2009内江)已知Rt△ABC的周长是,斜边上的中线长是2,则S△ABC=_____8_______。
1.(2010哈尔滨)如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为 125 度。
决胜中考篇
8. (2009宜宾)已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为 .
10.(2009临沂)如图,过原点的直线l与反比例函数的图像交于M,N两点,根据图像猜想线段MN的长的最小值是___________.
11.如下表,表中所给的每行的三个数a、b、c,有a<b<c,试根据表中已有数的规律,写出当a=27时,b,c的值,并把b、c用含a的代数式表示出来.
3,4,5 32+42=52
5,12,13 52+122=132
7,24,25 72+242=252
9,40,41 92+402=412
...... ……
27,b,c 272+b2=c2
解:当a=27时,b=364,c=365
,
12.如图,一架长5m的梯子AB,斜立在一竖直的墙上,这时梯子底端距墙底3m.如果梯子的顶端沿墙下滑1m,梯子的底端的水平方向沿一条直线也将滑动1m吗?如果梯子顶端下滑2 m呢?用所学知识,论证你的结论.
解:当梯子顶端下滑1米时,
如图,在Rt△ABC中,∠C=90°,
AB=5,BC=3,
所以由勾股定理得:
AC==4
梯子下滑后,如图,在Rt△DCE中,DE=5,DC=AC-1=3,
所以CE==4
所以梯子顶端下滑1m时,底端移动的距离为CE-BC=4-3=1 m.若梯子顶端下滑2 m,则AD=2,DC=4-2=2,此时
CE=
此时梯子滑动的距离为CE-BC=-3
12.(2009定西)如图13,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点。
求证:(1);
(2).
证明:(1) 因为∠ACB=∠ECD,
所以∠ACD+∠BCD=∠ACD+∠ACE.
即∠BCD=∠ACE.
因为BC=AC,DC=EC, 所以 △ACE≌△BCD.
(2)因为△ACB是等腰直角三角形,
所以∠B=∠BAC=45°.
因为 △ACE≌△BCD, 所以∠B=∠CAE=45°.
所以∠DAE=∠CAE+∠BAC= 45°+45°=90°.
所以.
由(1)知AE=DB,所以.
10.有一根70cm长的木棒,要放在长、宽、高分别是40cm、30cm、50cm的木盒中,能放进去吗?通过计算说明理由.
解:能放进去.
木盒中能放的最长的木棒的长度是DB′的长度.
在Rt△BDC中,BD= =
在Rt△BDB′中,由勾股定理得:B′D= = >70,
所以能放进去.
第3课时(共3课时)
课前预习篇
1.勾股定理在实际生活中应用非常广泛,要善于把实际问题转化为数学问题,特别是能准确的画出图形
2.数轴上的点不但可以表示__有理____数,也可以表示__无理____数,实数与数轴上的点是__一一对应______的.
典例剖析篇
【例1】如图,网格中的每个小正方形边长都是1,请在图中画出表示,这样的线段.
解:如图,AB、CD、EF,GH分别表示,.
【例2】台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市A的正南方向240千米B处有一台风中心,其中心最大风力为12级,每远离台风中心25千米,风力就会减弱一级,该台风中心现正以20千米/时的速度沿北偏东30°方向往C移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响.
(1)该城市是否会受到这次台风的影响?请说明理由.
(2)若会受到观风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受台风影响的最大风力为几级?
【解析】将实际问题转化为数学问题,利用勾股定理求解.
解:(1)作AH⊥BC于H
在Rt△ABH中,因为∠B=30°,
所以(千米)
又因为台风中心的影响半径为(12-4)×25=200(千米)
所以城市A要受台风影响.
(2)假设台风从M处开始影响A市,到N处结束,连接AM、AN.
在Rt△AMH中,
因为MH2=AM2-AH2=25600
所以MH=160(千米)
所以台风影响该城市的持续时间为(2×160)÷20=16(小时)
(3)该城市受台风影响的最大风力为12-120÷25=7.2(级)
基础夯实篇
1.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( C )
A.0
B.1
C.2
D.3
2.在测量旗杆的方案中,若旗杆高为21m,目测点到杆的距离为15m,则目测点到杆顶的距离为(设目高为1m) ( B )
A.20m B.25m C.30m D.35m
3.(2009恩施)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( B )
A. B.25 C. D.
4.木工师傅要做一个长方形桌面,做好后量得长为80cm,宽为60cm,对角线为100cm,则这个桌面 合格 .(填“合格”或“不合格” )
5.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了520m,求该河流的宽度为___480 m ______.
6.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高___15___米.
7.(2010德州)如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为__ 4___m.
决胜中考篇
8.(2009滨州)某楼梯的侧面视图如图4所示,其中AB=4 m,,,因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的长度应为 (2+2)米 .
9.(2009年安徽)13、长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了 m.
10.(2009安顺)图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是___76 .
11.(2010厦门)如图3,以第①个等腰直角三角形的斜边长作为第②个等腰直角三角形的腰,以第②个等腰直角三角形的斜边长做为第③个等腰直角三角形的腰,依次类推,若第⑨个等腰直角三角形的斜边长为厘米,则第①个等腰直角三角形的斜边长为 ______厘米.
12.在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中按下列要求画出图形.
(1)从点A出发画一条线段AB,使它的另一端点B在格点上,且长度为;
(2)画出所有的以(1)中的AB为边的等腰三角形,使另一个顶点在格点上,且令两边的长度都是无理数.
12.如图,某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点处有人求救,便立即派三名救生员前去营救.1号救生员从A点直接跳入海中;2号救生员沿岸边(岸边看成是直线)向前跑50米到C点,再跳入海中;3号救生员沿岸边向前跑200米到离B点最近的D点,再跳入海中.若三名救生员同时从A点出发,他们在岸边跑的速度都是5米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°,请你通过计算说明谁先到达营救地点B.
.解:在△ABD中,∠BAD=45°,, .
所以∠ABD=45°,BD=AD=200,
所以由勾股定理得:.
在中,,所以.
所以1号救生员到达B点所用的时间为(秒)
2号救生员到达B点所用的时间为(秒),
3号救生员到达B点所用的时间为(秒).
,所以2号救生员先到达营救地点.
13.中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?
解:在Rt△ABC中, BC2=AB2-AC2=502-302=1600,
所以BC=40
所以汽车的行驶速度为40÷2=20(m/s)=72(km/h)
因为72>70 所以小汽车超速了
答:这辆小汽车超速了.
14.(2009牡丹江)有一块直角三角形的绿地,量得两直角边长分别为现在要将绿地扩充成等腰三角形,且扩充部分是以为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
解:在Rt△ABC中,,由勾股定理有:,扩充部分为Rt△ABC,扩充成等腰△ABD.应分以下三种情况:①如图1,当AB=AD=10时,可求CD=CB=6,得△ABD的周长为32m.②如图2,当AB=BD=10时,可求CD=4,由勾股定理得:AD=4,得△ABD的周长为,③如图3,当AB为底时,设AD=BD=x,则CD=x-6,由勾股定理得:,得△ABD的周长为 m.
l
N
M
x
y
O
S3
S27S2
S11
c
b
a
a
a
a
b
b
b
c
c
c
c
b
a
c
c
a
b
c
a
b
c
a
b
c
a
b
c
B
D
C
A
c
b
5
20
15
10
C
A
B
A时
B时
B
C
A
30°
观测点
小汽车
小汽车
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 11 页) 版权所有@21世纪教育网
