六年级上册数学导学案 数与形(练习课) 人教版(表格式)
文档属性
| 名称 | 六年级上册数学导学案 数与形(练习课) 人教版(表格式) | 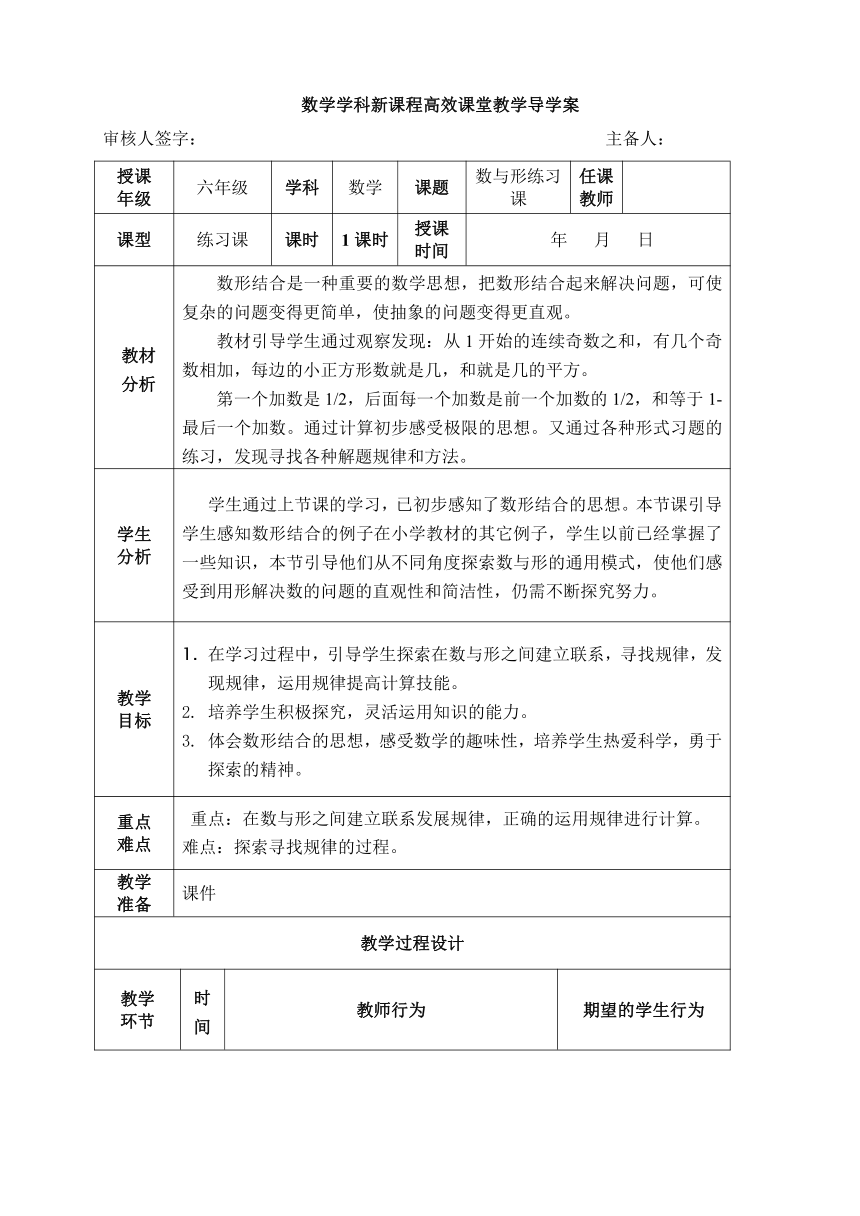 | |
| 格式 | doc | ||
| 文件大小 | 43.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 21:26:06 | ||
图片预览

文档简介
数学学科新课程高效课堂教学导学案
审核人签字: 主备人:
授课 年级 六年级 学科 数学 课题 数与形练习课 任课
教师
课型 练习课 课时 1课时 授课
时间 年 月 日
教材 分析 数形结合是一种重要的数学思想,把数形结合起来解决问题,可使复杂的问题变得更简单,使抽象的问题变得更直观。
教材引导学生通过观察发现:从1开始的连续奇数之和,有几个奇数相加,每边的小正方形数就是几,和就是几的平方。
第一个加数是1/2,后面每一个加数是前一个加数的1/2,和等于1-最后一个加数。通过计算初步感受极限的思想。又通过各种形式习题的练习,发现寻找各种解题规律和方法。
学生 分析 学生通过上节课的学习,已初步感知了数形结合的思想。本节课引导学生感知数形结合的例子在小学教材的其它例子,学生以前已经掌握了一些知识,本节引导他们从不同角度探索数与形的通用模式,使他们感受到用形解决数的问题的直观性和简洁性,仍需不断探究努力。
教学 目标 在学习过程中,引导学生探索在数与形之间建立联系,寻找规律,发现规律,运用规律提高计算技能。
培养学生积极探究,灵活运用知识的能力。
体会数形结合的思想,感受数学的趣味性,培养学生热爱科学,勇于探索的精神。
重点 难点 重点:在数与形之间建立联系发展规律,正确的运用规律进行计算。
难点:探索寻找规律的过程。
教学 准备 课件
教学过程设计
教学 环节 时
间 教师行为 期望的学生行为
复习旧知 创设情境
呈现目标 3分 回顾上节课总结的数形结合规律,计算1+3+5+7+……+1001=
用“无限接近”的思想,计算
+++……=
3.想一想,数与形的其它应用。 感受数形结合百般好,以形助数。关键弄清1001是第几个奇数,再利用规律解题。
记忆:几个连续奇数的和等于奇数个数的平方。
我们在其它哪些地方也用运了数形结合的思想。
自主探究小组讨论寻求方法 10分 1.平方数的变式练习,7?-5?,以形助数,就是内外两个正方形图中小正方形的个数差:第n个正方形图,每边有(2n+1)
个小正方形,,最外圈正方形的个数是:8n
2.第二题,第n个图中的小圆片总数是:1+2+3+……+n=(n+1)×n÷2 1.引导学生独立观察,自主探索,发现规律
2.小组合作,总结规律
3.师生共同总结公式。
基本训练提升能力 15分 3,引导总结;第n个图形,边长是n,周长就是3n
4.第4题,是等比例数列求和问题的变式。认识,相同时间内,小狗的路程是小亮的2倍。 3.第3题,每个图中三角形的个数正好是一个平方数,第n个图,含有n?个小三角形
4.使学生认识到:小狗与小亮的速度比是2:1,只要小狗途中没休息,当小亮行200米时,小狗能行400米。
拓展延伸巩固应用 10分 初步感受函数与图像的关系。
用连线的 方法解决抽象的问题,在解决问题过程中,先利用1盘的小兵,排除其他可能。
引导发现杨辉三角的规律:除第一个数外,每行中首项和末项都是1,其余各项均为上一行“双肩”上,两个数的和。 8.利用面积模型来理解一个完全平方公式。让学有余力的学生探索解释公式。
归纳概括提升意义 2分钟 数与形中隐藏着许多有趣的规律,我们要勇于探究,发现其中的秘密。帮助我们解决现实生活中的数学问题。 体会数学思想的价值与魅力。
教学 反思
审核人签字: 主备人:
授课 年级 六年级 学科 数学 课题 数与形练习课 任课
教师
课型 练习课 课时 1课时 授课
时间 年 月 日
教材 分析 数形结合是一种重要的数学思想,把数形结合起来解决问题,可使复杂的问题变得更简单,使抽象的问题变得更直观。
教材引导学生通过观察发现:从1开始的连续奇数之和,有几个奇数相加,每边的小正方形数就是几,和就是几的平方。
第一个加数是1/2,后面每一个加数是前一个加数的1/2,和等于1-最后一个加数。通过计算初步感受极限的思想。又通过各种形式习题的练习,发现寻找各种解题规律和方法。
学生 分析 学生通过上节课的学习,已初步感知了数形结合的思想。本节课引导学生感知数形结合的例子在小学教材的其它例子,学生以前已经掌握了一些知识,本节引导他们从不同角度探索数与形的通用模式,使他们感受到用形解决数的问题的直观性和简洁性,仍需不断探究努力。
教学 目标 在学习过程中,引导学生探索在数与形之间建立联系,寻找规律,发现规律,运用规律提高计算技能。
培养学生积极探究,灵活运用知识的能力。
体会数形结合的思想,感受数学的趣味性,培养学生热爱科学,勇于探索的精神。
重点 难点 重点:在数与形之间建立联系发展规律,正确的运用规律进行计算。
难点:探索寻找规律的过程。
教学 准备 课件
教学过程设计
教学 环节 时
间 教师行为 期望的学生行为
复习旧知 创设情境
呈现目标 3分 回顾上节课总结的数形结合规律,计算1+3+5+7+……+1001=
用“无限接近”的思想,计算
+++……=
3.想一想,数与形的其它应用。 感受数形结合百般好,以形助数。关键弄清1001是第几个奇数,再利用规律解题。
记忆:几个连续奇数的和等于奇数个数的平方。
我们在其它哪些地方也用运了数形结合的思想。
自主探究小组讨论寻求方法 10分 1.平方数的变式练习,7?-5?,以形助数,就是内外两个正方形图中小正方形的个数差:第n个正方形图,每边有(2n+1)
个小正方形,,最外圈正方形的个数是:8n
2.第二题,第n个图中的小圆片总数是:1+2+3+……+n=(n+1)×n÷2 1.引导学生独立观察,自主探索,发现规律
2.小组合作,总结规律
3.师生共同总结公式。
基本训练提升能力 15分 3,引导总结;第n个图形,边长是n,周长就是3n
4.第4题,是等比例数列求和问题的变式。认识,相同时间内,小狗的路程是小亮的2倍。 3.第3题,每个图中三角形的个数正好是一个平方数,第n个图,含有n?个小三角形
4.使学生认识到:小狗与小亮的速度比是2:1,只要小狗途中没休息,当小亮行200米时,小狗能行400米。
拓展延伸巩固应用 10分 初步感受函数与图像的关系。
用连线的 方法解决抽象的问题,在解决问题过程中,先利用1盘的小兵,排除其他可能。
引导发现杨辉三角的规律:除第一个数外,每行中首项和末项都是1,其余各项均为上一行“双肩”上,两个数的和。 8.利用面积模型来理解一个完全平方公式。让学有余力的学生探索解释公式。
归纳概括提升意义 2分钟 数与形中隐藏着许多有趣的规律,我们要勇于探究,发现其中的秘密。帮助我们解决现实生活中的数学问题。 体会数学思想的价值与魅力。
教学 反思
