人教版八年级上册:13.3.1等腰三角形 同步练习(附答案)
文档属性
| 名称 | 人教版八年级上册:13.3.1等腰三角形 同步练习(附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 192.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 00:00:00 | ||
图片预览



文档简介
13.3 等腰三角形
13.3.1 等腰三角形
第1课时 等腰三角形的性质
知识点1 等边对等角
1.若等腰三角形的顶角为40°,则它的底角度数为 ( )
A.40° B.50° C.60° D.70°
2.如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为 ( )
35858457620A.85° B.75°
C.60° D.30°
3.如图1是一把园林剪刀,把它抽象为图2,其中OA=OB.若剪刀张开的角为30°,则∠A= .
4.如图,在△ABC中,∠B=90°,AB=BD,AD=CD,求∠CAD的度数.
5.如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
知识点2 等腰三角形“三线合一”
6.如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是 ( )
27444707620A.∠B=∠C
B.AD⊥BC
C.AD平分∠BAC
D.AB=2BD
7.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D.若BD=2 cm,则CD= cm.
第7题图 第8题图
8.如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为 .
9.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
10.已知等腰三角形的一个外角为130°,则它的顶角的度数为 .
11.如图,在△ABC中,AB=AC,BD⊥AC于点D,∠A=50°,则∠DBC的度数为 .
12.如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为 ( )
A.30° B.45° C.50° D.75°
第12题图 第13题图
13.如图,在△ABC中,AB=AC,点E在BC边上,在线段AC的延长线上取点D,使得CD=CE,连接DE,CF是△CDE的中线.若∠FCE=52°,则∠A的度数为 ( )
A.38° B.34° C.32° D.28°
14.如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,则∠ABD= .
第14题图 第15题图
15.如图,在△ABC中,点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B= .
16.如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.求证:AD=AE.
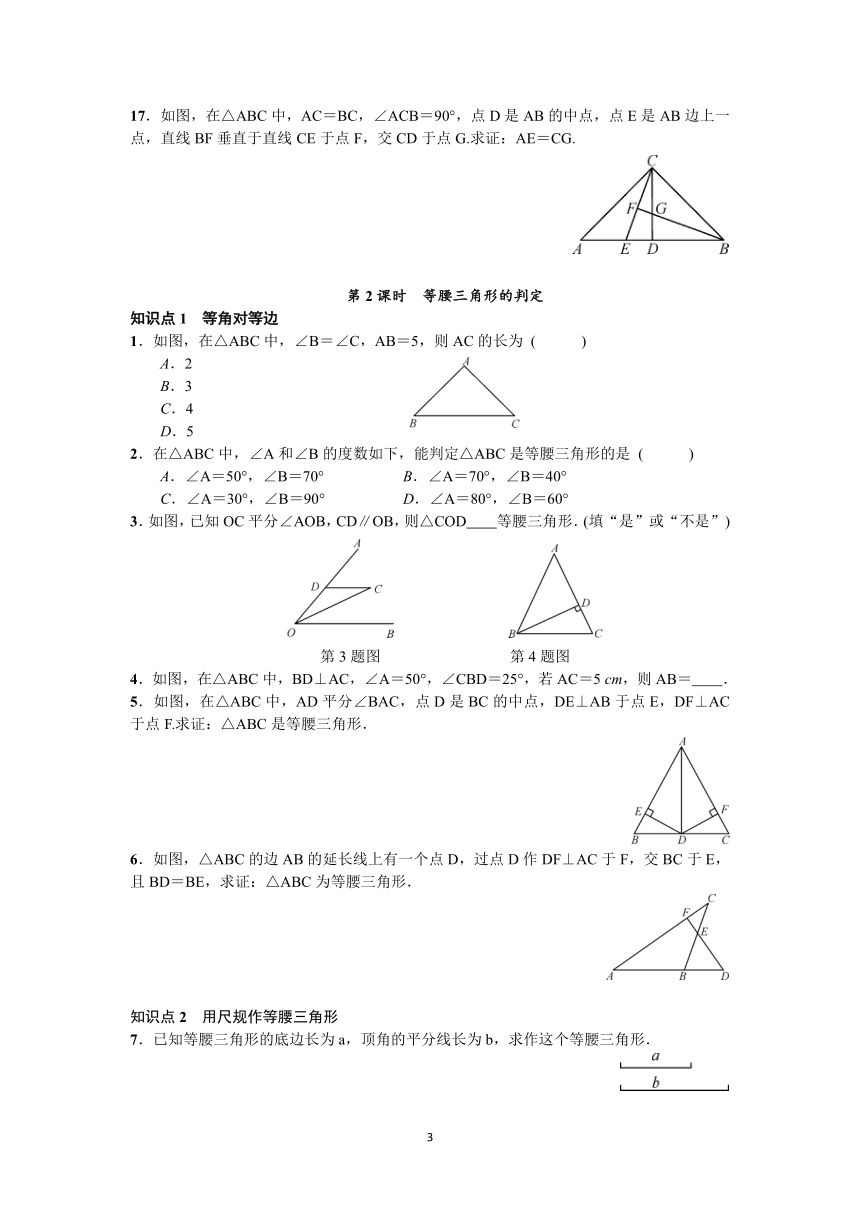
17.如图,在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点,直线BF垂直于直线CE于点F,交CD于点G.求证:AE=CG.
第2课时 等腰三角形的判定
知识点1 等角对等边
1.如图,在△ABC中,∠B=∠C,AB=5,则AC的长为 ( )
245491045720A.2
B.3
C.4
D.5
2.在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是 ( )
A.∠A=50°,∠B=70° B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90° D.∠A=80°,∠B=60°
3.如图,已知OC平分∠AOB,CD∥OB,则△COD 等腰三角形.(填“是”或“不是”)
第3题图 第4题图
4.如图,在△ABC中,BD⊥AC,∠A=50°,∠CBD=25°,若AC=5 cm,则AB= .
5.如图,在△ABC中,AD平分∠BAC,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F.求证:△ABC是等腰三角形.
6.如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,求证:△ABC为等腰三角形.
知识点2 用尺规作等腰三角形
7.已知等腰三角形的底边长为a,顶角的平分线长为b,求作这个等腰三角形.
25228552743208.如图,已知点P是射线ON上一动点(即P可在射线ON上运动),∠AON=45°,当∠A= 时,△AOP为等腰三角形.
9.如图,在△ABC中,∠B=∠C=40°,D,E是BC上的两点,且∠ADE=∠AED=80°,则图中共有等腰三角形 ( )
A.6个 B.5个 C.4个 D.3个
第9题图 第10题图
10.如图,在△ABC中,BP平分∠CBA,AP平分∠CAB,且DE∥AB,若CB=12,AC=18,则△CDE的周长是 .
11.如图,AD平分∠BAC,AD⊥BD,垂足为D,DE∥AC.求证:△BDE是等腰三角形.
12.如图,在△ABC中,AB=AC,∠BAC=36°,CD是∠ACD的平分线,交AB于点D,过点A作AE∥BC,交CD的延长线于点E.
(1)求∠ADC的度数;
(2)求证:AE=AC;
(3)试问△ADE是等腰三角形吗?请说明理由.
13.如图,OA平分∠BAC,∠1=∠2.求证:△ABC是等腰三角形.
参考答案
第1课时 等腰三角形的性质
1.D
2.B
3.75°.
4.解:∵△ABC中,∠B=90°,AB=BD,AD=CD,
∴∠BAD=∠ADB=45°,∠DCA=∠CAD.
∴∠BDA=2∠CAD=45°.
∴∠CAD=22.5°.
5.证明:∵AB=AC,
∴∠ABC=∠ACB.
∵BD=CD,
∴∠DBC=∠DCB.
∴∠ABC-∠DBC=∠ACB-∠DCB,
即∠ABD=∠ACD.
6.D
7.2
8.55°.
9.证明:∵AB=AC,
∴∠ABD=∠C.
又∵AD是BC边上的中线,
∴AD⊥BC.
∵BE⊥AC,∴∠BEC=∠ADB=90°.
∴∠C+∠CBE=∠ABD+∠BAD=90°.
∴∠CBE=∠BAD.
10.50°或80°.
11.25°.
12.B
13.D
14.35°.
15.37°.
16.证明:∵AB=AC,
∴∠B=∠C.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).
∴AD=AE.
17.证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,∠CAD=∠CBD=45°.
∴∠CAE=∠BCG.
又∵BF⊥CE,
∴∠CBG+∠BCF=90°.
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG.
在△AEC和△CGB中,
∴△AEC≌△CGB(ASA).
∴AE=CG.
第2课时 等腰三角形的判定
1.D
2.B
3.是
4.5__cm.
5.证明:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF.
∵点D是BC的中点,
∴BD=CD.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).
∴∠B=∠C.
∴AB=AC,即△ABC为等腰三角形.
6.证明:∵DF⊥AC,
∴∠DFA=∠EFC=90°.
∴∠A=∠EFC-∠D,
∠C=∠DFA-∠CEF.
∵BD=BE,
∴∠BED=∠D.
346392583820∵∠BED=∠CEF,
∴∠D=∠CEF.
∴∠A=∠C.
∴△ABC为等腰三角形.
7.解:①作线段AB=a;
②作线段AB的垂直平分线MN,与AB交于点D;
③以点D为圆心,b为半径画弧,交MN于点C;
④连接AC,BC,则△ABC就是所求作的三角形.
8.45°或67.5°或90°
9.C
10.30.
11.证明:∵DE∥AC,∴∠CAD=∠ADE.
∵AD平分∠BAC,
∴∠CAD=∠DAE.
∴∠ADE=∠DAE.
∵AD⊥BD,
∴∠DAE+∠B=90°,
∠ADE+∠BDE=90°.
∴∠B=∠BDE.
∴BE=DE,即△BDE是等腰三角形.
12.解:(1)∵AB=AC,∠BAC=36°,
∴∠B=∠ACB=(180°-∠BAC )=72°.
∵CD是∠ACB的平分线,
∴∠DCB=∠ACB=36°.
∴∠ADC=∠B+∠DCB=72°+36°=108°.
(2)证明:∵CD是∠ACB的平分线,
∴∠BCE=∠ACE.
∵AE∥BC,
∴∠BCE=∠E.
∴∠ACE=∠E.
∴AE=AC.
(3)△ADE是等腰三角形.
理由:∵AE∥BC,
∴∠EAB=∠B=72°.
∵∠B=72°,∠DCB=36°,
∴∠ADE=∠BDC=180°-72°-36°=72°.
∴∠EAD=∠ADE.
∴AE=DE.
∴△ADE是等腰三角形.
13.
证明:过点O作OD⊥AB于点D,OE⊥AC于点E,则△BOD和△COE都是直角三角形.
∵OA平分∠BAC,OD⊥AB,OE⊥AC,
∴OD=OE.
∵∠1=∠2,
∴OB=OC.
∴Rt△BOD≌Rt△COE(HL).
∴∠ABO=∠ACO.
又∵∠1=∠2,
∴∠ABC=∠ACB.
∴AB=AC.
∴△ABC是等腰三角形.
13.3.1 等腰三角形
第1课时 等腰三角形的性质
知识点1 等边对等角
1.若等腰三角形的顶角为40°,则它的底角度数为 ( )
A.40° B.50° C.60° D.70°
2.如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为 ( )
35858457620A.85° B.75°
C.60° D.30°
3.如图1是一把园林剪刀,把它抽象为图2,其中OA=OB.若剪刀张开的角为30°,则∠A= .
4.如图,在△ABC中,∠B=90°,AB=BD,AD=CD,求∠CAD的度数.
5.如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
知识点2 等腰三角形“三线合一”
6.如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是 ( )
27444707620A.∠B=∠C
B.AD⊥BC
C.AD平分∠BAC
D.AB=2BD
7.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D.若BD=2 cm,则CD= cm.
第7题图 第8题图
8.如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为 .
9.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
10.已知等腰三角形的一个外角为130°,则它的顶角的度数为 .
11.如图,在△ABC中,AB=AC,BD⊥AC于点D,∠A=50°,则∠DBC的度数为 .
12.如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为 ( )
A.30° B.45° C.50° D.75°
第12题图 第13题图
13.如图,在△ABC中,AB=AC,点E在BC边上,在线段AC的延长线上取点D,使得CD=CE,连接DE,CF是△CDE的中线.若∠FCE=52°,则∠A的度数为 ( )
A.38° B.34° C.32° D.28°
14.如图,在△ABC中,AB=BC,∠ABC=110°,AB的垂直平分线DE交AC于点D,连接BD,则∠ABD= .
第14题图 第15题图
15.如图,在△ABC中,点D在BC边上,BD=AD=AC,E为CD的中点.若∠CAE=16°,则∠B= .
16.如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.求证:AD=AE.
17.如图,在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点,直线BF垂直于直线CE于点F,交CD于点G.求证:AE=CG.
第2课时 等腰三角形的判定
知识点1 等角对等边
1.如图,在△ABC中,∠B=∠C,AB=5,则AC的长为 ( )
245491045720A.2
B.3
C.4
D.5
2.在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是 ( )
A.∠A=50°,∠B=70° B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90° D.∠A=80°,∠B=60°
3.如图,已知OC平分∠AOB,CD∥OB,则△COD 等腰三角形.(填“是”或“不是”)
第3题图 第4题图
4.如图,在△ABC中,BD⊥AC,∠A=50°,∠CBD=25°,若AC=5 cm,则AB= .
5.如图,在△ABC中,AD平分∠BAC,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F.求证:△ABC是等腰三角形.
6.如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,求证:△ABC为等腰三角形.
知识点2 用尺规作等腰三角形
7.已知等腰三角形的底边长为a,顶角的平分线长为b,求作这个等腰三角形.
25228552743208.如图,已知点P是射线ON上一动点(即P可在射线ON上运动),∠AON=45°,当∠A= 时,△AOP为等腰三角形.
9.如图,在△ABC中,∠B=∠C=40°,D,E是BC上的两点,且∠ADE=∠AED=80°,则图中共有等腰三角形 ( )
A.6个 B.5个 C.4个 D.3个
第9题图 第10题图
10.如图,在△ABC中,BP平分∠CBA,AP平分∠CAB,且DE∥AB,若CB=12,AC=18,则△CDE的周长是 .
11.如图,AD平分∠BAC,AD⊥BD,垂足为D,DE∥AC.求证:△BDE是等腰三角形.
12.如图,在△ABC中,AB=AC,∠BAC=36°,CD是∠ACD的平分线,交AB于点D,过点A作AE∥BC,交CD的延长线于点E.
(1)求∠ADC的度数;
(2)求证:AE=AC;
(3)试问△ADE是等腰三角形吗?请说明理由.
13.如图,OA平分∠BAC,∠1=∠2.求证:△ABC是等腰三角形.
参考答案
第1课时 等腰三角形的性质
1.D
2.B
3.75°.
4.解:∵△ABC中,∠B=90°,AB=BD,AD=CD,
∴∠BAD=∠ADB=45°,∠DCA=∠CAD.
∴∠BDA=2∠CAD=45°.
∴∠CAD=22.5°.
5.证明:∵AB=AC,
∴∠ABC=∠ACB.
∵BD=CD,
∴∠DBC=∠DCB.
∴∠ABC-∠DBC=∠ACB-∠DCB,
即∠ABD=∠ACD.
6.D
7.2
8.55°.
9.证明:∵AB=AC,
∴∠ABD=∠C.
又∵AD是BC边上的中线,
∴AD⊥BC.
∵BE⊥AC,∴∠BEC=∠ADB=90°.
∴∠C+∠CBE=∠ABD+∠BAD=90°.
∴∠CBE=∠BAD.
10.50°或80°.
11.25°.
12.B
13.D
14.35°.
15.37°.
16.证明:∵AB=AC,
∴∠B=∠C.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).
∴AD=AE.
17.证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,∠CAD=∠CBD=45°.
∴∠CAE=∠BCG.
又∵BF⊥CE,
∴∠CBG+∠BCF=90°.
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG.
在△AEC和△CGB中,
∴△AEC≌△CGB(ASA).
∴AE=CG.
第2课时 等腰三角形的判定
1.D
2.B
3.是
4.5__cm.
5.证明:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF.
∵点D是BC的中点,
∴BD=CD.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).
∴∠B=∠C.
∴AB=AC,即△ABC为等腰三角形.
6.证明:∵DF⊥AC,
∴∠DFA=∠EFC=90°.
∴∠A=∠EFC-∠D,
∠C=∠DFA-∠CEF.
∵BD=BE,
∴∠BED=∠D.
346392583820∵∠BED=∠CEF,
∴∠D=∠CEF.
∴∠A=∠C.
∴△ABC为等腰三角形.
7.解:①作线段AB=a;
②作线段AB的垂直平分线MN,与AB交于点D;
③以点D为圆心,b为半径画弧,交MN于点C;
④连接AC,BC,则△ABC就是所求作的三角形.
8.45°或67.5°或90°
9.C
10.30.
11.证明:∵DE∥AC,∴∠CAD=∠ADE.
∵AD平分∠BAC,
∴∠CAD=∠DAE.
∴∠ADE=∠DAE.
∵AD⊥BD,
∴∠DAE+∠B=90°,
∠ADE+∠BDE=90°.
∴∠B=∠BDE.
∴BE=DE,即△BDE是等腰三角形.
12.解:(1)∵AB=AC,∠BAC=36°,
∴∠B=∠ACB=(180°-∠BAC )=72°.
∵CD是∠ACB的平分线,
∴∠DCB=∠ACB=36°.
∴∠ADC=∠B+∠DCB=72°+36°=108°.
(2)证明:∵CD是∠ACB的平分线,
∴∠BCE=∠ACE.
∵AE∥BC,
∴∠BCE=∠E.
∴∠ACE=∠E.
∴AE=AC.
(3)△ADE是等腰三角形.
理由:∵AE∥BC,
∴∠EAB=∠B=72°.
∵∠B=72°,∠DCB=36°,
∴∠ADE=∠BDC=180°-72°-36°=72°.
∴∠EAD=∠ADE.
∴AE=DE.
∴△ADE是等腰三角形.
13.
证明:过点O作OD⊥AB于点D,OE⊥AC于点E,则△BOD和△COE都是直角三角形.
∵OA平分∠BAC,OD⊥AB,OE⊥AC,
∴OD=OE.
∵∠1=∠2,
∴OB=OC.
∴Rt△BOD≌Rt△COE(HL).
∴∠ABO=∠ACO.
又∵∠1=∠2,
∴∠ABC=∠ACB.
∴AB=AC.
∴△ABC是等腰三角形.
