五年级上册数学课件-4.1 简易方程(用字母表示数) 沪教版 (共30张PPT)
文档属性
| 名称 | 五年级上册数学课件-4.1 简易方程(用字母表示数) 沪教版 (共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 13:04:54 | ||
图片预览


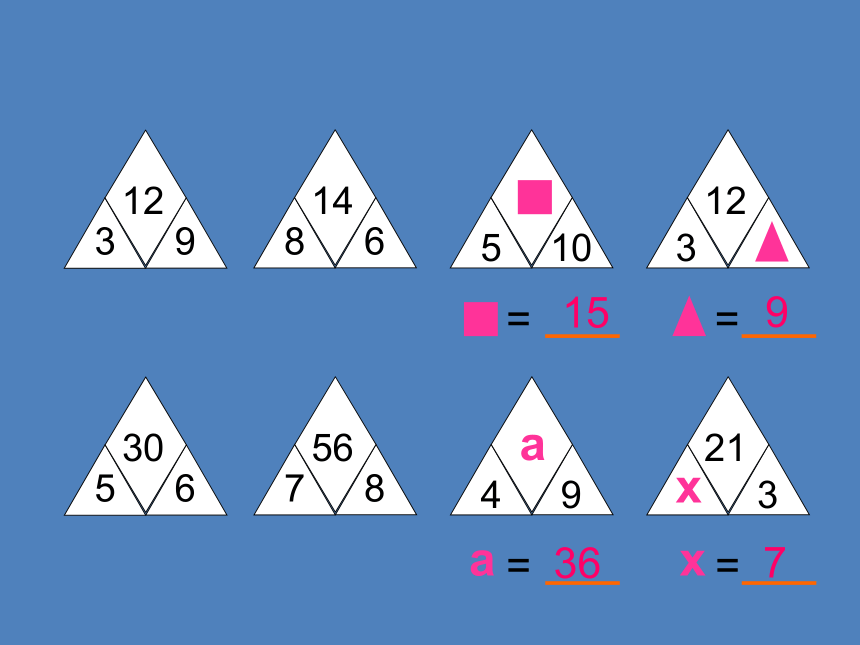







文档简介
生活中的字母
用字母表示数
E
A
B
C
X
F
Y
3
9
12
8
6
14
5
10
3
12
=
=
5
6
30
7
8
56
4
9
3
21
a
x
=
=
a
x
15
9
36
7
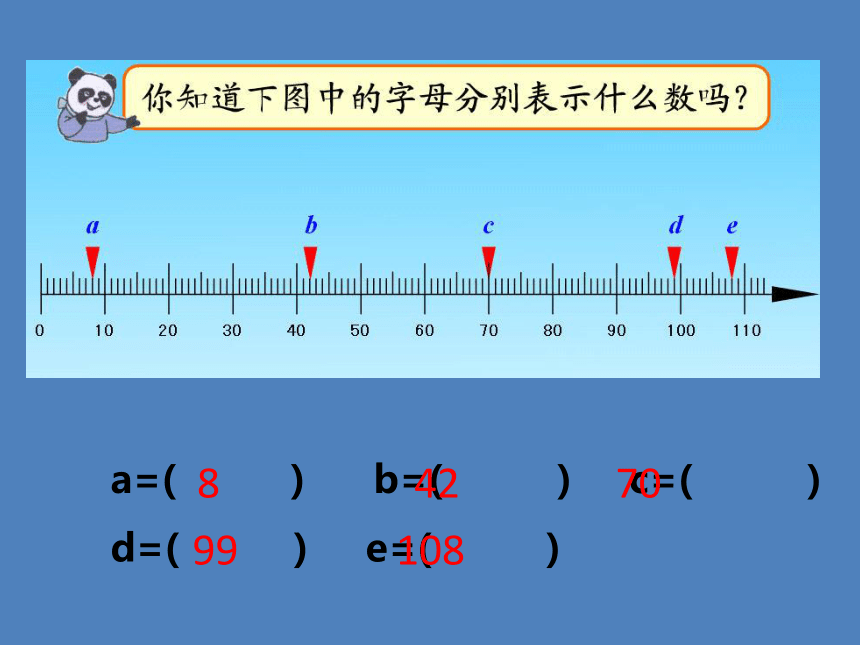
a=( ) b=( ) c=( )
d=( ) e=( )
8
42
70
99
108
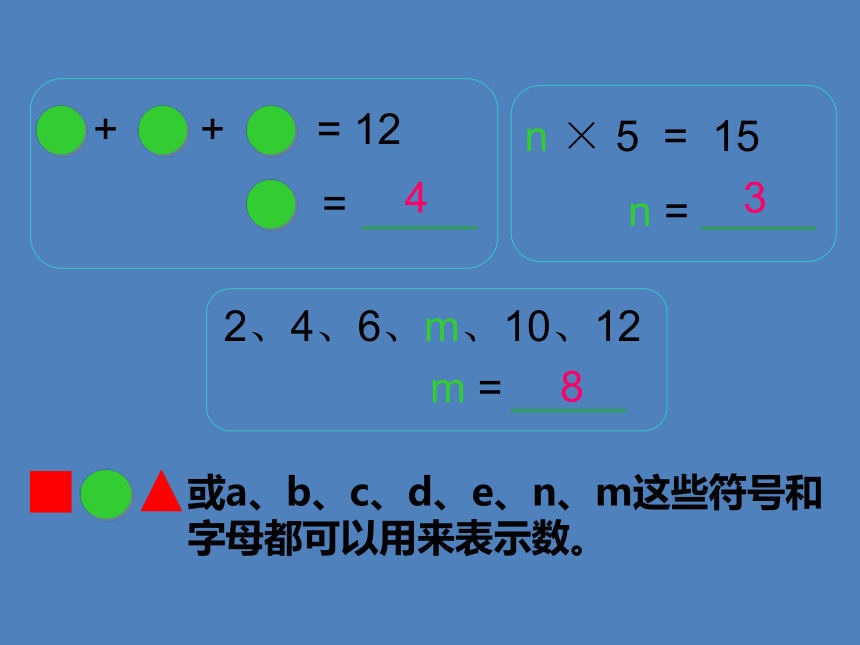
+
+
= 12
=
n × 5 = 15
n =
m =
2、4、6、m、10、12
或a、b、c、d、e、n、m这些符号和字母都可以用来表示数。
4
3
8
{8A107856-5554-42FB-B03E-39F5DBC370BA}长度单位
面积单位
质量单位
容量单位
千米
Km
平方千米
km2
吨
t
升
L
米
m
平方米
m2
千克
kg
毫升
ml
分米
dm
平方分米
dm2
克
g
厘米
cm
平方厘米
cm2
毫米
mm
为了书写方便,人们常用字母表示计量单位。
3+5=5+3
4+6=6+4
13+28=28+13
89+98=98+89
139+42=42+139
……
加法交换律:a+b=b+a
(3+5)+15=3+(5+15)
(7+6)+4=7+(6+4)
(13+28)+12=13+(28+12)
(89+98)+2=89+(98+2)
(139+42)+58=139+(42+58)
……
加法结合律(a+b)+c=a+(b+c)
3×5=5×3
4×6=6×4
13×28=28×13
89×98=98×89
139×42=42×139
……
乘法交换律:a×b=b×a
(3×5)×4=3×(5×4)
(7×125)×8=7×(125×8)
(13×5)×2=13×(5×2)
(89×4)×25=89×(4×25)
(139×25)×4=139×(25×4)
……
乘法结合律(a×b)×c=a×(b×c)
(125+25)×8=125×8+25×8
(7+125)×8=7×8+125×8
36×28+36×72=36×(28+72)
89×2+89×98=89×(2+98)
(139+25)×4=139×4+25×4
……
乘法分配律(a+b)×c=a×c+b×c
68-27-13=68-(27+13)
198-78-22=198-(78+22)
90-13-27=90-(13+27)
328-(28+68)=328-28-68
139-(39+33)=139-39-33
……
减法运算性质:a-b-c=a-(b+c)
68÷25÷4=68÷(25×4)
198÷125÷8=198÷(125×8)
90÷5÷2=90÷(5×2)
91÷(13×68)=91÷13÷68
150÷(50×33)=150÷50÷33
……
除法运算性质:a÷b÷c=a÷(b×c)
运算定律
用字母表示
简 写
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
减法运算性质
除法运算性质
a + b=b + a
(a+b)+c=a+(b+c)
a·b=b·a
ab=ba
(a·b)·c=a·(b·c)
(ab)c=a(bc)
(a + b)·c=a · c + b · c
(a + b)c=ac + bc
a×b=b×a
(a×b)×c=a×(b×c)
(a + b)×c=a×c + b×c
探究报告单
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a÷b÷c=a÷(b·c)
a÷b÷c=a÷(bc)
乘法交换律:a × b = b × a
在含有字母的式子里,字母与字母之间的乘号可以记作“ ·”,也可以省略不写。
a×b=b×a可以写成a·b=b·a或 ab = ba
运算定律
用字母表示
简 写
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
减法运算性质
除法运算性质
a + b=b + a
(a+b)+c=a+(b+c)
a·b=b·a
ab=ba
(a·b)·c=a·(b·c)
(ab)c=a(bc)
(a + b)·c=a · c + b · c
(a + b)c=ac + bc
a×b=b×a
(a×b)×c=a×(b×c)
(a + b)×c=a×c + b×c
探究报告单
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a÷b÷c=a÷(b·c)
a÷b÷c=a÷(bc)
用字母表示出正方形的面积和周长。
a
a
可以写成:
用S表示面积,用C表示周长。
S = a · a
C = 4 · a
读作:a的平方表示2个a相乘。
省略乘号时,一般把数写在字母前面。
S = a2
C = 4a
S = a × a
C = 4×a
注意:1×a或者a×1都写成a,不要写成1a。
用含有字母的式子来表示长方形的面积和周长
S = ________
C = ________
a
b
ab
2(a+b)
a2
两个a相乘
a×2( 即2a)
两个a相加
辩一辩
省略乘号,写出下面各式。
4×b
a×c
1×
d
χ
χ
×
×5
χ
n×6
=4b
=5
χ
=
d
χ
=
2
=
ac
=
6n
练一练
(1)42=4×2 ( ) (5)a×b=ab ( )
(2)7×7=72 ( ) (6)5+x=5x ( )
(3)a×a=a2 ( ) (7)a×b×3=ab3 ( )
(4)c×2=c2 ( ) (8) b×b读作2b ( )
×
×
×
a?
×
2c
√
×
×
3ab
×
b乘b
判断
6×6 6?
X×2 x?
10? 10×2
b? b+b
2b b×b
x×x x+x
10+10 10×10
连线
含有字母式子的简写规则
规则一
在含有字母的式子里,字母与字母之间的乘号可以记作“·”,也可以省略不写。
规则二
在含有字母的式子里,数字与字母之间的乘号也可以记作“·”,或者省略不写。
在省略乘号的时候,数要写在字母的前面。
注意
1×a或者a×1都可以写成a,一般不写成1a。
注意
两个相同字母相乘,可以写成这个字母的平方。
如:a×a=a?,a?读作a的平方,表示2个a相乘。
拓展
χ=( )
χ
?
你知道最早有意识地系统使用字母来表
示数的人是谁吗?他就是法国数学家韦
达。韦达一生致 力于对数学的研究,做
出了很多重要贡献,成为那个时代最伟
大的数学家。自从韦达系统使用字母表
示数后,引出了大量的数学发现,解决
了很多古代的复杂问题。
你知道吗
共勉
+
+
=
A代表成功,
X代表艰苦的劳动,
Y代表正确的方法,
Z代表少说空话。
用字母表示数
E
A
B
C
X
F
Y
3
9
12
8
6
14
5
10
3
12
=
=
5
6
30
7
8
56
4
9
3
21
a
x
=
=
a
x
15
9
36
7
a=( ) b=( ) c=( )
d=( ) e=( )
8
42
70
99
108
+
+
= 12
=
n × 5 = 15
n =
m =
2、4、6、m、10、12
或a、b、c、d、e、n、m这些符号和字母都可以用来表示数。
4
3
8
{8A107856-5554-42FB-B03E-39F5DBC370BA}长度单位
面积单位
质量单位
容量单位
千米
Km
平方千米
km2
吨
t
升
L
米
m
平方米
m2
千克
kg
毫升
ml
分米
dm
平方分米
dm2
克
g
厘米
cm
平方厘米
cm2
毫米
mm
为了书写方便,人们常用字母表示计量单位。
3+5=5+3
4+6=6+4
13+28=28+13
89+98=98+89
139+42=42+139
……
加法交换律:a+b=b+a
(3+5)+15=3+(5+15)
(7+6)+4=7+(6+4)
(13+28)+12=13+(28+12)
(89+98)+2=89+(98+2)
(139+42)+58=139+(42+58)
……
加法结合律(a+b)+c=a+(b+c)
3×5=5×3
4×6=6×4
13×28=28×13
89×98=98×89
139×42=42×139
……
乘法交换律:a×b=b×a
(3×5)×4=3×(5×4)
(7×125)×8=7×(125×8)
(13×5)×2=13×(5×2)
(89×4)×25=89×(4×25)
(139×25)×4=139×(25×4)
……
乘法结合律(a×b)×c=a×(b×c)
(125+25)×8=125×8+25×8
(7+125)×8=7×8+125×8
36×28+36×72=36×(28+72)
89×2+89×98=89×(2+98)
(139+25)×4=139×4+25×4
……
乘法分配律(a+b)×c=a×c+b×c
68-27-13=68-(27+13)
198-78-22=198-(78+22)
90-13-27=90-(13+27)
328-(28+68)=328-28-68
139-(39+33)=139-39-33
……
减法运算性质:a-b-c=a-(b+c)
68÷25÷4=68÷(25×4)
198÷125÷8=198÷(125×8)
90÷5÷2=90÷(5×2)
91÷(13×68)=91÷13÷68
150÷(50×33)=150÷50÷33
……
除法运算性质:a÷b÷c=a÷(b×c)
运算定律
用字母表示
简 写
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
减法运算性质
除法运算性质
a + b=b + a
(a+b)+c=a+(b+c)
a·b=b·a
ab=ba
(a·b)·c=a·(b·c)
(ab)c=a(bc)
(a + b)·c=a · c + b · c
(a + b)c=ac + bc
a×b=b×a
(a×b)×c=a×(b×c)
(a + b)×c=a×c + b×c
探究报告单
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a÷b÷c=a÷(b·c)
a÷b÷c=a÷(bc)
乘法交换律:a × b = b × a
在含有字母的式子里,字母与字母之间的乘号可以记作“ ·”,也可以省略不写。
a×b=b×a可以写成a·b=b·a或 ab = ba
运算定律
用字母表示
简 写
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
减法运算性质
除法运算性质
a + b=b + a
(a+b)+c=a+(b+c)
a·b=b·a
ab=ba
(a·b)·c=a·(b·c)
(ab)c=a(bc)
(a + b)·c=a · c + b · c
(a + b)c=ac + bc
a×b=b×a
(a×b)×c=a×(b×c)
(a + b)×c=a×c + b×c
探究报告单
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a÷b÷c=a÷(b·c)
a÷b÷c=a÷(bc)
用字母表示出正方形的面积和周长。
a
a
可以写成:
用S表示面积,用C表示周长。
S = a · a
C = 4 · a
读作:a的平方表示2个a相乘。
省略乘号时,一般把数写在字母前面。
S = a2
C = 4a
S = a × a
C = 4×a
注意:1×a或者a×1都写成a,不要写成1a。
用含有字母的式子来表示长方形的面积和周长
S = ________
C = ________
a
b
ab
2(a+b)
a2
两个a相乘
a×2( 即2a)
两个a相加
辩一辩
省略乘号,写出下面各式。
4×b
a×c
1×
d
χ
χ
×
×5
χ
n×6
=4b
=5
χ
=
d
χ
=
2
=
ac
=
6n
练一练
(1)42=4×2 ( ) (5)a×b=ab ( )
(2)7×7=72 ( ) (6)5+x=5x ( )
(3)a×a=a2 ( ) (7)a×b×3=ab3 ( )
(4)c×2=c2 ( ) (8) b×b读作2b ( )
×
×
×
a?
×
2c
√
×
×
3ab
×
b乘b
判断
6×6 6?
X×2 x?
10? 10×2
b? b+b
2b b×b
x×x x+x
10+10 10×10
连线
含有字母式子的简写规则
规则一
在含有字母的式子里,字母与字母之间的乘号可以记作“·”,也可以省略不写。
规则二
在含有字母的式子里,数字与字母之间的乘号也可以记作“·”,或者省略不写。
在省略乘号的时候,数要写在字母的前面。
注意
1×a或者a×1都可以写成a,一般不写成1a。
注意
两个相同字母相乘,可以写成这个字母的平方。
如:a×a=a?,a?读作a的平方,表示2个a相乘。
拓展
χ=( )
χ
?
你知道最早有意识地系统使用字母来表
示数的人是谁吗?他就是法国数学家韦
达。韦达一生致 力于对数学的研究,做
出了很多重要贡献,成为那个时代最伟
大的数学家。自从韦达系统使用字母表
示数后,引出了大量的数学发现,解决
了很多古代的复杂问题。
你知道吗
共勉
+
+
=
A代表成功,
X代表艰苦的劳动,
Y代表正确的方法,
Z代表少说空话。
同课章节目录
