24.2 直角三角形的性质 课件(共16张PPT)
文档属性
| 名称 | 24.2 直角三角形的性质 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 16:18:27 | ||
图片预览






文档简介
(共16张PPT)
24.2
直角三角形的性质
华东师大版
九年级数学上册
教学课件
学习目标:
(1)掌握直角三角形的性质定理,并能灵活运用.
(2)继续学习几何证明的分析方法,懂得推理过程中的因果关系.知道数学内容中普遍存在的运动、变化、相互联系和相互转化的规律.
学习重点:
直角三角形斜边上的中线性质定理的应用.
学习难点:
直角三角形斜边上的中线性质定理的证明思
方法.
新课导入
归纳已经学过的直角三角形的性质.
回顾
(1)直角三角形的两个锐角互余.
(2)直角三角形两直角边的平方和等于斜边的平方(勾股定理).
直角三角形还具备哪些特殊性质呢,接下来我们一起探索.
探索
画出Rt△ABC,并画出斜边AB上的中线CD,量一量,看看CD与AB有什么关系.
A
B
C
D
发现
CD恰好是AB的一半.
验证
A
B
C
D
已知,如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD=
AB.
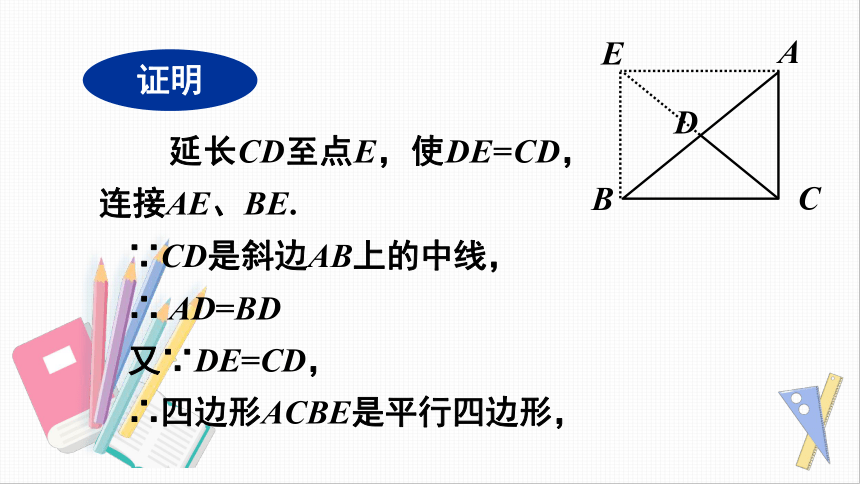
证明
A
B
C
D
E
延长CD至点E,使DE=CD,连接AE、BE.
∵CD是斜边AB上的中线,
∴
AD=BD
又∵DE=CD,
∴四边形ACBE是平行四边形,
A
B
C
D
E
又∵∠ACB=90°,
∴四边形ACBE是矩形,
∴CE=AB,
∴CD=
CE=
AB
由此,我们得到直角三角形的又一条性质:
(3)直角三角形斜边上的中线等于斜边的一半.
例
如图,在Rt△ACB中,∠ACB=90°,∠A=30°.
求证:BC=
AB
A
B
C
证明
作斜边AB上的中线CD,
∵∠A=30°,
∴∠B=60°,
∴△CBD是等边三角形.
A
B
C
D
则CD=
AB=AD=BD.(性质3)
∴BC=BD=
AB.
由此可知:直角三角形中,30°角所对的直角边等于斜边的一半.
1.已知直角三角形两条直角边的长分别为1cm和
cm.求斜边上中线的长.
随堂演练
解:设斜边长为x,则
x2=12+(
)2
x2=4
解得x
=
2
由直角三角形斜边上的中线等于斜边的一半可知,斜边上中线的长为1cm.
2.小明沿倾斜角为30°的山坡,从山脚步行到山顶的革命烈士纪念碑,共走了120m.求山顶的高度.
解:由题意可画出如图的直角三角形.
其中AB=120m,∠B=30°.
由30°角所对直角边等于斜边的
一半可知AC=60m.
即山顶的高度为60m.
A
B
C
课堂小结
1.直角三角形斜边上的中线等于斜边的一半.
2.直角三角形中,30°角所对的直角边等于斜边的一半.
3.有斜边上的中点,要考虑构造斜边上的中线或中位线.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本课从复习已学过的直角三角形的性质入手,通过实验操作、猜想、证明探究直角三角形斜边上的中线性质定理,培养学生识图的能力,提高分析和解决问题的能力,在积极参与定理的学习活动中,不断增强主体意识和综合意识.
谢谢欣赏
24.2
直角三角形的性质
华东师大版
九年级数学上册
教学课件
学习目标:
(1)掌握直角三角形的性质定理,并能灵活运用.
(2)继续学习几何证明的分析方法,懂得推理过程中的因果关系.知道数学内容中普遍存在的运动、变化、相互联系和相互转化的规律.
学习重点:
直角三角形斜边上的中线性质定理的应用.
学习难点:
直角三角形斜边上的中线性质定理的证明思
方法.
新课导入
归纳已经学过的直角三角形的性质.
回顾
(1)直角三角形的两个锐角互余.
(2)直角三角形两直角边的平方和等于斜边的平方(勾股定理).
直角三角形还具备哪些特殊性质呢,接下来我们一起探索.
探索
画出Rt△ABC,并画出斜边AB上的中线CD,量一量,看看CD与AB有什么关系.
A
B
C
D
发现
CD恰好是AB的一半.
验证
A
B
C
D
已知,如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD=
AB.
证明
A
B
C
D
E
延长CD至点E,使DE=CD,连接AE、BE.
∵CD是斜边AB上的中线,
∴
AD=BD
又∵DE=CD,
∴四边形ACBE是平行四边形,
A
B
C
D
E
又∵∠ACB=90°,
∴四边形ACBE是矩形,
∴CE=AB,
∴CD=
CE=
AB
由此,我们得到直角三角形的又一条性质:
(3)直角三角形斜边上的中线等于斜边的一半.
例
如图,在Rt△ACB中,∠ACB=90°,∠A=30°.
求证:BC=
AB
A
B
C
证明
作斜边AB上的中线CD,
∵∠A=30°,
∴∠B=60°,
∴△CBD是等边三角形.
A
B
C
D
则CD=
AB=AD=BD.(性质3)
∴BC=BD=
AB.
由此可知:直角三角形中,30°角所对的直角边等于斜边的一半.
1.已知直角三角形两条直角边的长分别为1cm和
cm.求斜边上中线的长.
随堂演练
解:设斜边长为x,则
x2=12+(
)2
x2=4
解得x
=
2
由直角三角形斜边上的中线等于斜边的一半可知,斜边上中线的长为1cm.
2.小明沿倾斜角为30°的山坡,从山脚步行到山顶的革命烈士纪念碑,共走了120m.求山顶的高度.
解:由题意可画出如图的直角三角形.
其中AB=120m,∠B=30°.
由30°角所对直角边等于斜边的
一半可知AC=60m.
即山顶的高度为60m.
A
B
C
课堂小结
1.直角三角形斜边上的中线等于斜边的一半.
2.直角三角形中,30°角所对的直角边等于斜边的一半.
3.有斜边上的中点,要考虑构造斜边上的中线或中位线.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本课从复习已学过的直角三角形的性质入手,通过实验操作、猜想、证明探究直角三角形斜边上的中线性质定理,培养学生识图的能力,提高分析和解决问题的能力,在积极参与定理的学习活动中,不断增强主体意识和综合意识.
谢谢欣赏
