24.4.1解直角三角形 课件(共18张ppt)
文档属性
| 名称 | 24.4.1解直角三角形 课件(共18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 541.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 15:28:52 | ||
图片预览






文档简介
(共18张PPT)
第1课时
解直角三角形
24.4
解直角三角形
华东师大版
九年级数学上册
教学课件
学习目标:
1.使学生理解解直角三角形的意义;
2.能运用直角三角形的三个关系式解直角三
角形.
学习重点:
用直角三角形的三个关系式解直角三角形.
学习难点:
用直角三角形的有关知识去解决简单的实际
问题.
新课导入
三边之间关系
锐角之间关系
边角之间关系
(以锐角A为例)
a2+b2=c2(勾股定理)
∠A+∠B=90?
回顾
直角三角形的有关性质及边角关系.
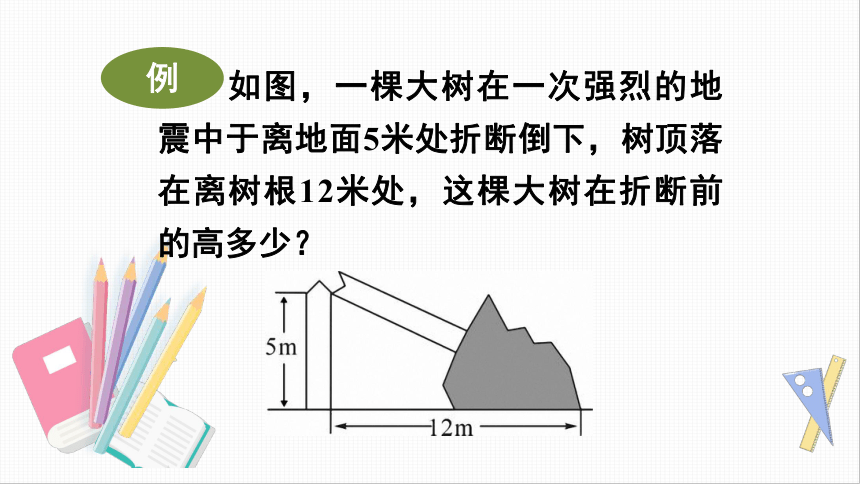
例
如图,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根12米处,这棵大树在折断前的高多少?
解
利用勾股定理可以求出折断后倒下部分的长度为
13+5=18(米)
答:大树在折断之前高18米.
1、在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三形
;
3、在直角三角形中,如果已知两条边的长度,那么就可利用勾股定理求出另外的一条边。
2、在解决实际问题时,应“先画图,再求解”;
总结
例
如图,在相距2000米东西两炮台A、B处同时发现入侵敌舰C,在炮台A处测得敌舰C在它的南偏东40°的方向,在炮台B处测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米).
解
在Rt△ABC中,
∵∠CAB=90°-∠DAC=50°
=
tan∠CAB,
∴BC
=
AB·tan∠CAB=2000×tan50°≈2384(米)
∵
=
cos50°,
∴AC=
≈3111(米)
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.
总结
解直角三形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角.
根据三角形全等的判定,由于已知一个角是直角,所以在以上两种情况下,对应的直角三角形唯一确定.因此,可以求出其他元素.
1.在电线杆离地面8米高处向地面拉一条缆绳,缆绳和地面成53°7′角,求该缆绳的长及缆绳地面固定点到电线杆底部的距离.(精确到0.1米)
随堂演练
解:由题意可得右图直角三角形
8m
53°7′
A
C
B
即缆绳长10米,缆绳地面固定点到电线杆底部的距离为6.0米
2.海船以32.6海里/时的速度向正北方向航行,在A处看灯塔Q在海船北偏东30°处,半小时后航行到B处,发现此时灯塔Q与海船的距离最短,求灯塔Q到B处的距离(画出图形后计算,精确到0.1海里).
解:由题意得Rt△ABQ如右图
A
Q
B
30°
AB=32.6×0.5=16.3(海里)
设BQ为x海里,则AQ=2x海里
x2+16.32=(2x)2
解得x
≈
9.4
即灯塔Q到B的距离为9.4海里.
课堂小结
1.“解直角三角形”是求出直角三角形的所有元素.
2.解直角三角形的条件是除直角外的两个元素,且至少需要一边,即已知两边或已知一边和一锐角.
3.解直角三角形的方法.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
通过直角三角形边角之间关系的复习和例题的实践应用,归纳出“解直角三角形”的含义和两种解题情况.通过讨论交流得出解直角三角形的方法,并学会把实际问题转化为直角三角形的问题.给出一定的情景内容,引导学生自主探究,通过例题的实践应用,提高学生分析问题、解决问题的能力,以及提高综合运用知识的能力.
谢谢欣赏
第1课时
解直角三角形
24.4
解直角三角形
华东师大版
九年级数学上册
教学课件
学习目标:
1.使学生理解解直角三角形的意义;
2.能运用直角三角形的三个关系式解直角三
角形.
学习重点:
用直角三角形的三个关系式解直角三角形.
学习难点:
用直角三角形的有关知识去解决简单的实际
问题.
新课导入
三边之间关系
锐角之间关系
边角之间关系
(以锐角A为例)
a2+b2=c2(勾股定理)
∠A+∠B=90?
回顾
直角三角形的有关性质及边角关系.
例
如图,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根12米处,这棵大树在折断前的高多少?
解
利用勾股定理可以求出折断后倒下部分的长度为
13+5=18(米)
答:大树在折断之前高18米.
1、在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三形
;
3、在直角三角形中,如果已知两条边的长度,那么就可利用勾股定理求出另外的一条边。
2、在解决实际问题时,应“先画图,再求解”;
总结
例
如图,在相距2000米东西两炮台A、B处同时发现入侵敌舰C,在炮台A处测得敌舰C在它的南偏东40°的方向,在炮台B处测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米).
解
在Rt△ABC中,
∵∠CAB=90°-∠DAC=50°
=
tan∠CAB,
∴BC
=
AB·tan∠CAB=2000×tan50°≈2384(米)
∵
=
cos50°,
∴AC=
≈3111(米)
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.
总结
解直角三形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角.
根据三角形全等的判定,由于已知一个角是直角,所以在以上两种情况下,对应的直角三角形唯一确定.因此,可以求出其他元素.
1.在电线杆离地面8米高处向地面拉一条缆绳,缆绳和地面成53°7′角,求该缆绳的长及缆绳地面固定点到电线杆底部的距离.(精确到0.1米)
随堂演练
解:由题意可得右图直角三角形
8m
53°7′
A
C
B
即缆绳长10米,缆绳地面固定点到电线杆底部的距离为6.0米
2.海船以32.6海里/时的速度向正北方向航行,在A处看灯塔Q在海船北偏东30°处,半小时后航行到B处,发现此时灯塔Q与海船的距离最短,求灯塔Q到B处的距离(画出图形后计算,精确到0.1海里).
解:由题意得Rt△ABQ如右图
A
Q
B
30°
AB=32.6×0.5=16.3(海里)
设BQ为x海里,则AQ=2x海里
x2+16.32=(2x)2
解得x
≈
9.4
即灯塔Q到B的距离为9.4海里.
课堂小结
1.“解直角三角形”是求出直角三角形的所有元素.
2.解直角三角形的条件是除直角外的两个元素,且至少需要一边,即已知两边或已知一边和一锐角.
3.解直角三角形的方法.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
通过直角三角形边角之间关系的复习和例题的实践应用,归纳出“解直角三角形”的含义和两种解题情况.通过讨论交流得出解直角三角形的方法,并学会把实际问题转化为直角三角形的问题.给出一定的情景内容,引导学生自主探究,通过例题的实践应用,提高学生分析问题、解决问题的能力,以及提高综合运用知识的能力.
谢谢欣赏
