24.4解直角三角形 第2课时 俯角和仰角问题 上课课件
文档属性
| 名称 | 24.4解直角三角形 第2课时 俯角和仰角问题 上课课件 |  | |
| 格式 | zip | ||
| 文件大小 | 331.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 15:24:27 | ||
图片预览




文档简介
(共14张PPT)
第2课时
俯角和仰角问题
华东师大版
九年级数学上册
教学课件
学习目标:
1.理解仰角、俯角的含义,准确运用这些概
念来解决一些实际问题.
2.培养学生将实际问题抽象成数学模型并进
行解释与应用的能力.
学习重点:
理解仰角和俯角的概念.
学习难点:
能解与直角三角形有关的实际问题.
新课导入
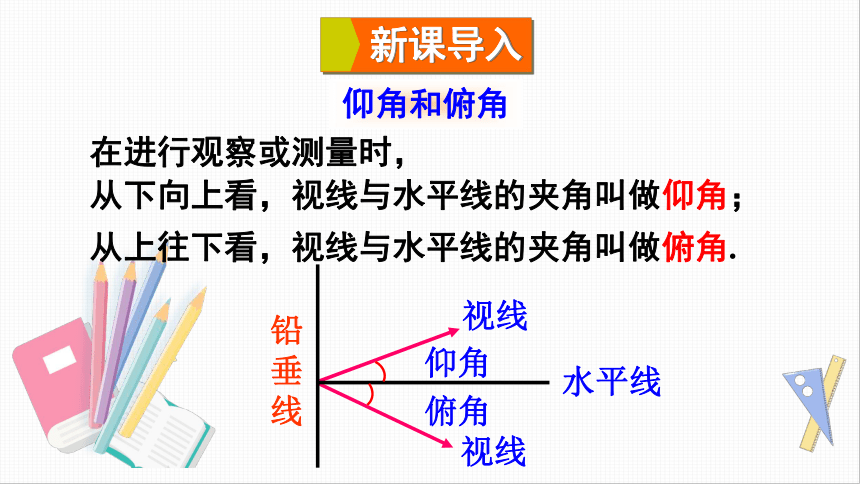
仰角和俯角
在进行观察或测量时,
从上往下看,视线与水平线的夹角叫做俯角.
从下向上看,视线与水平线的夹角叫做仰角;
铅垂线
水平线
视线
视线
仰角
俯角
例
如图,为了测量旗杆的高度BC,在离旗杆10米的A处,用高1.50米的测角仪DA测得旗杆顶端C的仰角α=52°,求旗杆BC的高.(精确到0.1米)
C
A
B
D
E
52°
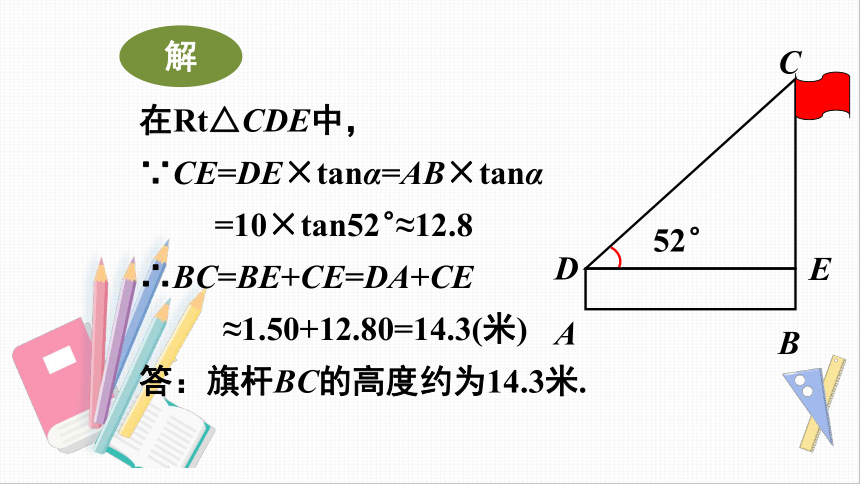
解
在Rt△CDE中,
∵CE=DE×tanα=AB×tanα
=10×tan52°≈12.8
∴BC=BE+CE=DA+CE
≈1.50+12.80=14.3(米)
答:旗杆BC的高度约为14.3米.
C
A
B
D
E
52°
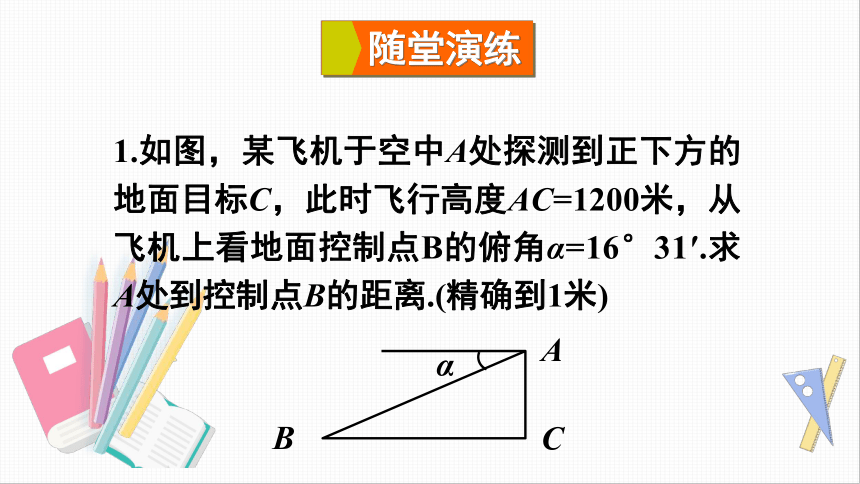
1.如图,某飞机于空中A处探测到正下方的地面目标C,此时飞行高度AC=1200米,从飞机上看地面控制点B的俯角α=16°31′.求A处到控制点B的距离.(精确到1米)
随堂演练
α
A
C
B
α
A
C
B
解:由图可知,∠B=α=16°31′
2.两座建筑物DA与CB,其地面距离DC为50.4米,从DA的顶点A测得CB顶部B的仰角α=20°,测得其底部C的俯角β=35°.求这两座建筑物的高.(精确到0.1米)
C
B
A
D
α
β
50.4
E
则AD=EC=AE·tanβ≈50.4×0.7≈35.3(米)
C
B
A
D
α
β
50.4
E
解:如图AD=EC,
Rt△AEC中,tanβ=
Rt△ABE中,tanα=
则BE=AE·tanα≈50.4×0.36≈18.1(米)
BC=EC+BE=35.3+18.1=53.4(米)
课堂小结
铅垂线
水平线
视线
视线
仰角
俯角
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本节课从学生接受知识的最近发展区出发,创设了学生最熟悉的旗杆问题情境,引导学生发现问题、分析问题.在探索活动中,学生自主探索知识,逐步把生活实际问题抽象成数学模型并进行解释与应用的学习方法,养成交流与合作的良好习惯.让学生在学习过程中感受到成功的喜悦,产生后继学习的激情,增强学数学的信心.
谢谢欣赏
第2课时
俯角和仰角问题
华东师大版
九年级数学上册
教学课件
学习目标:
1.理解仰角、俯角的含义,准确运用这些概
念来解决一些实际问题.
2.培养学生将实际问题抽象成数学模型并进
行解释与应用的能力.
学习重点:
理解仰角和俯角的概念.
学习难点:
能解与直角三角形有关的实际问题.
新课导入
仰角和俯角
在进行观察或测量时,
从上往下看,视线与水平线的夹角叫做俯角.
从下向上看,视线与水平线的夹角叫做仰角;
铅垂线
水平线
视线
视线
仰角
俯角
例
如图,为了测量旗杆的高度BC,在离旗杆10米的A处,用高1.50米的测角仪DA测得旗杆顶端C的仰角α=52°,求旗杆BC的高.(精确到0.1米)
C
A
B
D
E
52°
解
在Rt△CDE中,
∵CE=DE×tanα=AB×tanα
=10×tan52°≈12.8
∴BC=BE+CE=DA+CE
≈1.50+12.80=14.3(米)
答:旗杆BC的高度约为14.3米.
C
A
B
D
E
52°
1.如图,某飞机于空中A处探测到正下方的地面目标C,此时飞行高度AC=1200米,从飞机上看地面控制点B的俯角α=16°31′.求A处到控制点B的距离.(精确到1米)
随堂演练
α
A
C
B
α
A
C
B
解:由图可知,∠B=α=16°31′
2.两座建筑物DA与CB,其地面距离DC为50.4米,从DA的顶点A测得CB顶部B的仰角α=20°,测得其底部C的俯角β=35°.求这两座建筑物的高.(精确到0.1米)
C
B
A
D
α
β
50.4
E
则AD=EC=AE·tanβ≈50.4×0.7≈35.3(米)
C
B
A
D
α
β
50.4
E
解:如图AD=EC,
Rt△AEC中,tanβ=
Rt△ABE中,tanα=
则BE=AE·tanα≈50.4×0.36≈18.1(米)
BC=EC+BE=35.3+18.1=53.4(米)
课堂小结
铅垂线
水平线
视线
视线
仰角
俯角
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
教学反思
本节课从学生接受知识的最近发展区出发,创设了学生最熟悉的旗杆问题情境,引导学生发现问题、分析问题.在探索活动中,学生自主探索知识,逐步把生活实际问题抽象成数学模型并进行解释与应用的学习方法,养成交流与合作的良好习惯.让学生在学习过程中感受到成功的喜悦,产生后继学习的激情,增强学数学的信心.
谢谢欣赏
