25.2 .3列举所有机会均等的结果 课件(共25张)
文档属性
| 名称 | 25.2 .3列举所有机会均等的结果 课件(共25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 556.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
3.列举所有机会均等的结果
华东师大版
九年级数学上册
教学课件
25.2
随机事件的概率
学习目标:
理解并掌握列表法和树状图法求随机事件的概率,并利用它们解决问题,正确认识在什么条件下使用列表法,什么条件下使用树状图法.
学习重点:
会用列表法和树状图法求随机事件的概率.
区分什么时候用列表法,什么时候用树状图法求概率.
学习难点:
列表法是如何列表,树状图的画法.
列表法和树状图的选取方法.
新课导入
抛掷一枚普通硬币3次.有人说“连续掷出三个正面”和“先掷出两个正面,再掷出一个反面”的概率是一样的.你同意吗?
例4
分析
3次抛掷,每次可能出现的结果都是正面或反面,而且每次出现正面或反面的概率相等,树状图中每一条路径就是一种可能的结果.
正
反
正
反
正
反
正
反
正
反
正
反
正
反
第①枚
②
③
树状图
解
抛掷一枚普通硬币3次,共有以下8种机会均等的结果:
正正正,正正反,正反正,正反反,
反正正,反正反,反反正,反反反.
P(正正正)=
P(正正反)=
所以,例题中的说法正确.
思考
有的同学认为:抛掷三枚普通硬币,硬币落地后只可能出现4种结果:(1)全是正面;(2)两正一反;
(3)两反一正;(4)全是反面.
因此这四个事件出现的概率相等.你同意这种说法吗?为什么?
不同意;四种情况出现的概率并不均等,(1)(4)出现的几率要小于(2)(3).
问题
口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,放回搅匀,再摸出第2个球,两次摸球就可能出现3种结果:
(1)都是红球;(2)都是白球;
(3)一红一白.
这三个事件发生的概率相等吗?
思考
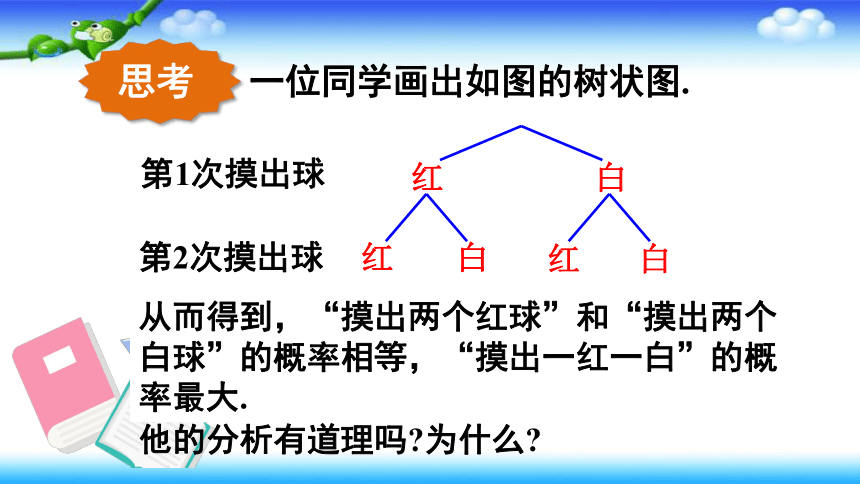
一位同学画出如图的树状图.
红
白
红
白
红
白
第1次摸出球
第2次摸出球
从而得到,“摸出两个红球”和“摸出两个白球”的概率相等,“摸出一红一白”的概率最大.
他的分析有道理吗?为什么?
把两个白球分别记作白1和白2,画出如下的树状图.
第1次摸出球
第2次摸出球
从图中可以看出,一共有9种等可能的结果.
分析
红
白2
白1
红
白2
红
红
白1
白1
白2
白1
白2
在“摸出两红”、“摸出两白”、“摸出一红一白”这三个事件中,“摸出_____”的概率最小,等于______,“摸出________”和“摸出_________”的概率相等,都是______.
两红
一红一白
两白
结论
问题
投掷两枚普通的正方体骰子.掷得的点数之积有多少种可能?点数之积为多少的概率最大,其概率是多少?
用列举法来得出所有可能的点数之积.
分析
×
1
2
3
4
5
6
1
1
2
3
4
5
6
2
2
4
6
8
10
12
3
3
6
9
12
15
18
4
4
8
12
16
20
24
5
5
10
15
20
25
30
6
6
12
18
24
30
36
由上表可以看出积为______的概率最大,其概率等于_______.
6或12
结论
问题
“石头、剪刀、布”的游戏中,假定甲乙两人每次都是等可能地做这三种手势,那么一次比赛两人做同种手势(即不分胜负)的概率是多少?
分析
画出如图的树状图:
甲
乙
结果
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
(石头,石头)
(石头,剪刀)
(石头,布)
(剪刀,石头)
(剪刀,剪刀)
(剪刀,布)
(布,石头)
(布,剪刀)
(布,布)
结论
所有机会均等的结果有9种,其中的3种——(石头,石头)、(剪刀,剪刀)、(布,布)是我们关注的结果.
所以P(同种手势)=
随堂演练
1.同时投掷两枚普通的正四面体骰子,求下列事件的概率:
(1)所得点数之和恰为偶数;
(2)所得点数之和恰为奇数;
(3)所得点数之和恰为质数;
+
1
2
3
4
1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
(1)P(和为偶数)=
(2)P(和为奇数)=
(3)P(和为质数)=
2.在九九乘法表的45个运算结果中随意抽取1个,将下列事件的概率从小到大排序:
(1)恰为偶数;(2)恰为奇数;
(3)小于10;(4)大于100;
(5)个位数是0;(6)3的倍数.
(1)P(恰为偶数)=
(2)P(恰为奇数)=
(3)P(小于10)=
(4)P(大于100)=
(5)P(个位数是0)=
(6)P(3的倍数)=
课堂小结
1.一次试验中可能出现的结果是有限多个,各种结果发生的可能性是相等的.通常可用列表法和树状图法求得各种可能结果.
2.注意第二次放回与不放回的区别.
3.一次实验中涉及3个或更多个因素时,不重不漏地求出所有可能的结果,通常采用树状图法.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
本课通过生活实例引入新课,激发学生的学习兴趣,通过例题分析用树状图法和列表法求概率的具体步骤和方法.并比较它们的优劣,让学生有比较地掌握方法,让学生理解更深刻.
教学反思
谢谢欣赏
3.列举所有机会均等的结果
华东师大版
九年级数学上册
教学课件
25.2
随机事件的概率
学习目标:
理解并掌握列表法和树状图法求随机事件的概率,并利用它们解决问题,正确认识在什么条件下使用列表法,什么条件下使用树状图法.
学习重点:
会用列表法和树状图法求随机事件的概率.
区分什么时候用列表法,什么时候用树状图法求概率.
学习难点:
列表法是如何列表,树状图的画法.
列表法和树状图的选取方法.
新课导入
抛掷一枚普通硬币3次.有人说“连续掷出三个正面”和“先掷出两个正面,再掷出一个反面”的概率是一样的.你同意吗?
例4
分析
3次抛掷,每次可能出现的结果都是正面或反面,而且每次出现正面或反面的概率相等,树状图中每一条路径就是一种可能的结果.
正
反
正
反
正
反
正
反
正
反
正
反
正
反
第①枚
②
③
树状图
解
抛掷一枚普通硬币3次,共有以下8种机会均等的结果:
正正正,正正反,正反正,正反反,
反正正,反正反,反反正,反反反.
P(正正正)=
P(正正反)=
所以,例题中的说法正确.
思考
有的同学认为:抛掷三枚普通硬币,硬币落地后只可能出现4种结果:(1)全是正面;(2)两正一反;
(3)两反一正;(4)全是反面.
因此这四个事件出现的概率相等.你同意这种说法吗?为什么?
不同意;四种情况出现的概率并不均等,(1)(4)出现的几率要小于(2)(3).
问题
口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,放回搅匀,再摸出第2个球,两次摸球就可能出现3种结果:
(1)都是红球;(2)都是白球;
(3)一红一白.
这三个事件发生的概率相等吗?
思考
一位同学画出如图的树状图.
红
白
红
白
红
白
第1次摸出球
第2次摸出球
从而得到,“摸出两个红球”和“摸出两个白球”的概率相等,“摸出一红一白”的概率最大.
他的分析有道理吗?为什么?
把两个白球分别记作白1和白2,画出如下的树状图.
第1次摸出球
第2次摸出球
从图中可以看出,一共有9种等可能的结果.
分析
红
白2
白1
红
白2
红
红
白1
白1
白2
白1
白2
在“摸出两红”、“摸出两白”、“摸出一红一白”这三个事件中,“摸出_____”的概率最小,等于______,“摸出________”和“摸出_________”的概率相等,都是______.
两红
一红一白
两白
结论
问题
投掷两枚普通的正方体骰子.掷得的点数之积有多少种可能?点数之积为多少的概率最大,其概率是多少?
用列举法来得出所有可能的点数之积.
分析
×
1
2
3
4
5
6
1
1
2
3
4
5
6
2
2
4
6
8
10
12
3
3
6
9
12
15
18
4
4
8
12
16
20
24
5
5
10
15
20
25
30
6
6
12
18
24
30
36
由上表可以看出积为______的概率最大,其概率等于_______.
6或12
结论
问题
“石头、剪刀、布”的游戏中,假定甲乙两人每次都是等可能地做这三种手势,那么一次比赛两人做同种手势(即不分胜负)的概率是多少?
分析
画出如图的树状图:
甲
乙
结果
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
(石头,石头)
(石头,剪刀)
(石头,布)
(剪刀,石头)
(剪刀,剪刀)
(剪刀,布)
(布,石头)
(布,剪刀)
(布,布)
结论
所有机会均等的结果有9种,其中的3种——(石头,石头)、(剪刀,剪刀)、(布,布)是我们关注的结果.
所以P(同种手势)=
随堂演练
1.同时投掷两枚普通的正四面体骰子,求下列事件的概率:
(1)所得点数之和恰为偶数;
(2)所得点数之和恰为奇数;
(3)所得点数之和恰为质数;
+
1
2
3
4
1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
(1)P(和为偶数)=
(2)P(和为奇数)=
(3)P(和为质数)=
2.在九九乘法表的45个运算结果中随意抽取1个,将下列事件的概率从小到大排序:
(1)恰为偶数;(2)恰为奇数;
(3)小于10;(4)大于100;
(5)个位数是0;(6)3的倍数.
(1)P(恰为偶数)=
(2)P(恰为奇数)=
(3)P(小于10)=
(4)P(大于100)=
(5)P(个位数是0)=
(6)P(3的倍数)=
课堂小结
1.一次试验中可能出现的结果是有限多个,各种结果发生的可能性是相等的.通常可用列表法和树状图法求得各种可能结果.
2.注意第二次放回与不放回的区别.
3.一次实验中涉及3个或更多个因素时,不重不漏地求出所有可能的结果,通常采用树状图法.
课后作业
1.从教材习题中选取,
2.完成练习册本课时的习题.
本课通过生活实例引入新课,激发学生的学习兴趣,通过例题分析用树状图法和列表法求概率的具体步骤和方法.并比较它们的优劣,让学生有比较地掌握方法,让学生理解更深刻.
教学反思
谢谢欣赏
