山东省潍坊市昌乐2020--2021学年九年级(上)数学青岛版期中模拟试题(word版含答案)
文档属性
| 名称 | 山东省潍坊市昌乐2020--2021学年九年级(上)数学青岛版期中模拟试题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 185.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 00:00:00 | ||
图片预览

文档简介
12407900106045002020--2021学年山东省潍坊市昌乐九年级(上)数学期中模拟试题(2)
一、选择题(每题3分,共24分)
1.如图所示,在△ABC中∠BAC=90°,D是BC中点,AE⊥AD交CB延长线于E点,则下列结论正确的是( )
A.△AED∽△ACB B.△AEB∽△ACD
C.△BAE∽△ACE D.△AEC∽△DAC
2.如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A,false,AC=3,则CD长为( )
A.1 B.false C.2 D.false
第1题图 第2题图
3.等腰三角形底边与底边上的高的比是2:,则顶角为 ( )
A. 60° B.90° C.120° D.150°
4.一段公路的坡度为1:3,某人沿这段公路路面前进100米,那么他上升的最大高度是( )
A.30米 B.10米 C.米 D.米
5.若平行四边形相邻两边的长分别为10和15,它们的夹角为60°,则平行四边形的面积是( )
A.150??? ? B.??? C. 9???? D. 7
6.⊙O的直径是15cm,CD经过圆心O,与⊙O交于C、D两点,垂直弦AB于M,且OM:OC=3 :5,则AB=( )
A.24cm B.12cm C.6cm D.3cm
7.⊙O的直径是3,直线与⊙O相交,圆心O到直线的距离是d,则d应满足( )
A.d>3 B.1.5 8.半径相等的圆的内接正三角形,正方形边长之比为( )
A.1:false B.:false C.3:2 D.1:2
二、填空题(每题3分,共18分)
9.falsecos45°-falsetan60°= ;
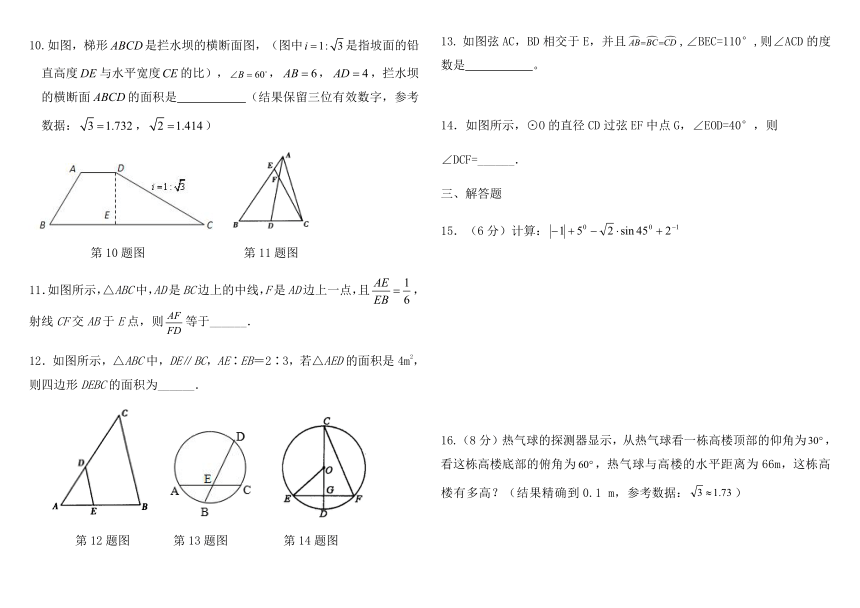
10.如图,梯形false是拦水坝的横断面图,(图中false是指坡面的铅直高度false与水平宽度false的比),false,false,false,拦水坝的横断面false的面积是 (结果保留三位有效数字,参考数据:false,false)
第10题图 第11题图
11.如图所示,△ABC中,AD是BC边上的中线,F是AD边上一点,且false,射线CF交AB于E点,则false等于______.
12.如图所示,△ABC中,DE∥BC,AE∶EB=2∶3,若△AED的面积是4m2,则四边形DEBC的面积为______.
第12题图 第13题图 第14题图
如图弦AC,BD相交于E,并且false,∠BEC=110°,则∠ACD的度数是 。
14.如图所示,⊙O的直径CD过弦EF中点G,∠EOD=40°,则
∠DCF=______.
三、解答题
15.(6分)计算:
16.(8分)热气球的探测器显示,从热气球看一栋高楼顶部的仰角为,看这栋高楼底部的俯角为,热气球与高楼的水平距离为66m,这栋高楼有多高?(结果精确到0.1 m,参考数据:)
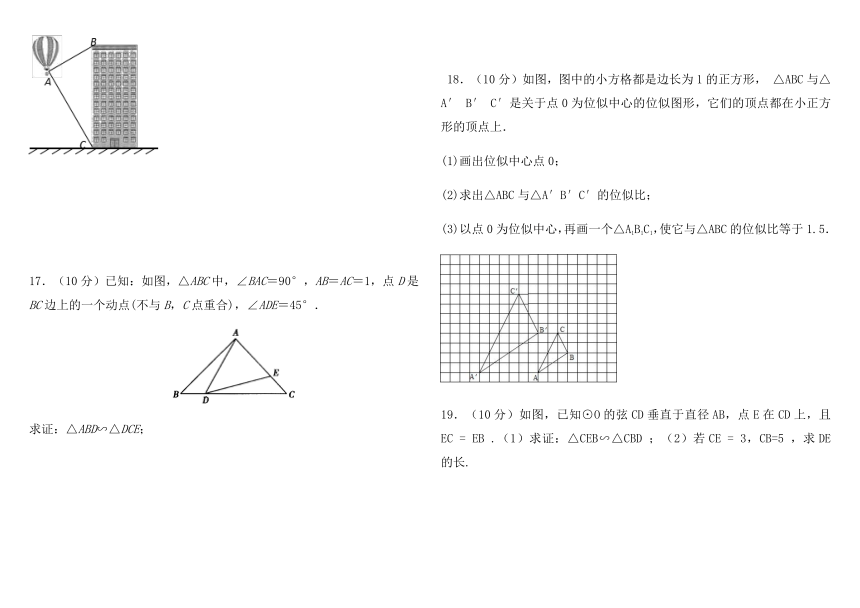
17.(10分)已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.
求证:△ABD∽△DCE;
18.(10分)如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
19.(10分)如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC = EB .(1)求证:△CEB∽△CBD ;(2)若CE = 3,CB=5 ,求DE的长.
20.(10分)如图,一艘轮船在海上以每小时36海里的速度向正西方向航行,上午8时,在B处测得小岛A在北偏东300方向,之后轮船继续向正西方向航行,于上午9时到达C处,这时测得小岛A 在北偏东600方向.如果轮船仍继续向正西方向航行,于上午11时到达D处,这时轮船与小岛A相距多远?
21.(12分)如图所示,AB是⊙O的直径,BC切⊙O于B,AC交⊙O于P,E是BC 边上的中点,连结PE,PE与⊙O相切吗?若相切,请加以证明,若不相切,请说明理由.
22.(12分)如图,已知:⊙D交y轴于A、B,交x轴于C,过点C的直线:y=-2false-8 与y轴交于点P.
(1)试判断PC与⊙D的位置关系.
(2)判断在直线PC上是否存在点E,使得S△EOP=4S△CDO,若存在,求出点E的坐标;若不存在,请说明理由.
答案
C. 2.C.3.A 4.D 5.B 6.B 7.C 8.B
false, 10. 52.0, 11.false , 12.21m2 , 13. 75°,14.20°
15. ,
16.false,
17.提示:除∠B=∠C外,证∠ADB=∠DEC.
18.(1)提示:位似中心在各组对应点连线的交点处.(2)位似比为1:2.(3)略.
19.(1)证明:∵弦CD垂直于直径AB ∴BC=BD ∴∠C =∠D 又∵EC = EB ∴∠C =∠CBE ∴∠D =∠CBE 又∵∠C =∠C ∴△CEB∽△CBD
(2)解:∵△CEB ∽△CBD ∴false ∴CD=false ∴DE = CD-CE =false-3 =false
20.轮船与小岛A相距130海里
21.解:相切,证OP⊥PE即可.
12. (1)PC与⊙D相切,理由:令x=0,得y=-8,故P(0,-8);令y=0,得x=-2false,
故C(-2false,0),故OP=8,OC=2false,CD=1,
∴CD=false=3,
又PC=false,
∴PC2+CD2=9+72=81=PD2.
从而∠PCD=90°,故PC与⊙D相切.
(2)存在.点E(false,-12)或(-false,-4),使S△EOP=4S△CDO.
设E点坐标为(x,y),过E作EF⊥y轴于F,则EF=│x│.
∴S△POE=falsePO·EF=4│x│.
∵S△CDO=falseCO·DO=false.
∴4│x│=4false,│x│=false,x=±false,
当x=-false 时,y=-2false×(-false)-8=-4 ;
当x=false 时,y=-2false×false-8=-12 .
故E点坐标为(-false,-4)或(false,-12).
一、选择题(每题3分,共24分)
1.如图所示,在△ABC中∠BAC=90°,D是BC中点,AE⊥AD交CB延长线于E点,则下列结论正确的是( )
A.△AED∽△ACB B.△AEB∽△ACD
C.△BAE∽△ACE D.△AEC∽△DAC
2.如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A,false,AC=3,则CD长为( )
A.1 B.false C.2 D.false
第1题图 第2题图
3.等腰三角形底边与底边上的高的比是2:,则顶角为 ( )
A. 60° B.90° C.120° D.150°
4.一段公路的坡度为1:3,某人沿这段公路路面前进100米,那么他上升的最大高度是( )
A.30米 B.10米 C.米 D.米
5.若平行四边形相邻两边的长分别为10和15,它们的夹角为60°,则平行四边形的面积是( )
A.150??? ? B.??? C. 9???? D. 7
6.⊙O的直径是15cm,CD经过圆心O,与⊙O交于C、D两点,垂直弦AB于M,且OM:OC=3 :5,则AB=( )
A.24cm B.12cm C.6cm D.3cm
7.⊙O的直径是3,直线与⊙O相交,圆心O到直线的距离是d,则d应满足( )
A.d>3 B.1.5
A.1:false B.:false C.3:2 D.1:2
二、填空题(每题3分,共18分)
9.falsecos45°-falsetan60°= ;
10.如图,梯形false是拦水坝的横断面图,(图中false是指坡面的铅直高度false与水平宽度false的比),false,false,false,拦水坝的横断面false的面积是 (结果保留三位有效数字,参考数据:false,false)
第10题图 第11题图
11.如图所示,△ABC中,AD是BC边上的中线,F是AD边上一点,且false,射线CF交AB于E点,则false等于______.
12.如图所示,△ABC中,DE∥BC,AE∶EB=2∶3,若△AED的面积是4m2,则四边形DEBC的面积为______.
第12题图 第13题图 第14题图
如图弦AC,BD相交于E,并且false,∠BEC=110°,则∠ACD的度数是 。
14.如图所示,⊙O的直径CD过弦EF中点G,∠EOD=40°,则
∠DCF=______.
三、解答题
15.(6分)计算:
16.(8分)热气球的探测器显示,从热气球看一栋高楼顶部的仰角为,看这栋高楼底部的俯角为,热气球与高楼的水平距离为66m,这栋高楼有多高?(结果精确到0.1 m,参考数据:)
17.(10分)已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.
求证:△ABD∽△DCE;
18.(10分)如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
19.(10分)如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC = EB .(1)求证:△CEB∽△CBD ;(2)若CE = 3,CB=5 ,求DE的长.
20.(10分)如图,一艘轮船在海上以每小时36海里的速度向正西方向航行,上午8时,在B处测得小岛A在北偏东300方向,之后轮船继续向正西方向航行,于上午9时到达C处,这时测得小岛A 在北偏东600方向.如果轮船仍继续向正西方向航行,于上午11时到达D处,这时轮船与小岛A相距多远?
21.(12分)如图所示,AB是⊙O的直径,BC切⊙O于B,AC交⊙O于P,E是BC 边上的中点,连结PE,PE与⊙O相切吗?若相切,请加以证明,若不相切,请说明理由.
22.(12分)如图,已知:⊙D交y轴于A、B,交x轴于C,过点C的直线:y=-2false-8 与y轴交于点P.
(1)试判断PC与⊙D的位置关系.
(2)判断在直线PC上是否存在点E,使得S△EOP=4S△CDO,若存在,求出点E的坐标;若不存在,请说明理由.
答案
C. 2.C.3.A 4.D 5.B 6.B 7.C 8.B
false, 10. 52.0, 11.false , 12.21m2 , 13. 75°,14.20°
15. ,
16.false,
17.提示:除∠B=∠C外,证∠ADB=∠DEC.
18.(1)提示:位似中心在各组对应点连线的交点处.(2)位似比为1:2.(3)略.
19.(1)证明:∵弦CD垂直于直径AB ∴BC=BD ∴∠C =∠D 又∵EC = EB ∴∠C =∠CBE ∴∠D =∠CBE 又∵∠C =∠C ∴△CEB∽△CBD
(2)解:∵△CEB ∽△CBD ∴false ∴CD=false ∴DE = CD-CE =false-3 =false
20.轮船与小岛A相距130海里
21.解:相切,证OP⊥PE即可.
12. (1)PC与⊙D相切,理由:令x=0,得y=-8,故P(0,-8);令y=0,得x=-2false,
故C(-2false,0),故OP=8,OC=2false,CD=1,
∴CD=false=3,
又PC=false,
∴PC2+CD2=9+72=81=PD2.
从而∠PCD=90°,故PC与⊙D相切.
(2)存在.点E(false,-12)或(-false,-4),使S△EOP=4S△CDO.
设E点坐标为(x,y),过E作EF⊥y轴于F,则EF=│x│.
∴S△POE=falsePO·EF=4│x│.
∵S△CDO=falseCO·DO=false.
∴4│x│=4false,│x│=false,x=±false,
当x=-false 时,y=-2false×(-false)-8=-4 ;
当x=false 时,y=-2false×false-8=-12 .
故E点坐标为(-false,-4)或(false,-12).
同课章节目录
