北师大版七年级数学上册第二章 有理数及其运算 复习练习题(Word版 含简单答案)
文档属性
| 名称 | 北师大版七年级数学上册第二章 有理数及其运算 复习练习题(Word版 含简单答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 168.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 00:00:00 | ||
图片预览



文档简介
北师大版七年级数学上册第二章
有理数及其运算
复习练习题
一.选择题(共22小题)
1.下列四个算式:①﹣2﹣3=﹣1;②2﹣|﹣3|=﹣1;③(﹣2)3=﹣6;④﹣2÷=﹣6.其中,正确的算式有( )
A.0个
B.1个
C.2个
D.3个
2.如图,半径为1的圆从表示3的点开始沿着数轴向左滚动一周,圆上的点A与表示3的点重合,滚动一周后到达点B,点B表示的数是( )
A.﹣2π
B.3﹣2π
C.﹣3﹣2π
D.﹣3+2π
3.在数轴上表示有理数a,b,c的点如图所示,若ac<0,b+c<0,则下列式子一定成立的是( )
A.a+c>0
B.a+c<0
C.abc<0
D.|b|<|c|
4.数轴上原点左边有一点A,点A对应着数a,有如下说法:
①﹣a表示的数一定是一个正数.
②若|a|=9时,则a=﹣9.
③在﹣a,,a2,a3中,最大的数值是a2.
④式子|a+|的最小值为2.
其中正确的个数是( )
A.1
B.2
C.3
D.4
5.如果a,b互为相反数,x,y互为倒数,m的倒数等于它本身,则6(a+b)+m2﹣3xy的值是( )
A.﹣2
B.﹣1
C.0
D.1
6.x是数轴上任意一点表示的数,若|x﹣3|+|x+2|的值最小,则x的取值范围是( )
A.x≥3
B.x≤﹣2
C.﹣2≤x≤3
D.﹣2<x<3
7.当|a|=5,|b|=7,且|a+b|=a+b,则a﹣b的值为( )
A.﹣12
B.﹣2或﹣12
C.2
D.﹣2
8.如果a+b+c=0,且|a|>|b|>|c|.则下列说法中可能成立的是( )
A.b为正数,c为负数
B.c为正数,b为负数
C.c为正数,a为负数
D.c为负数,a为负数
9.下列说法中,正确的是( )
A.一个有理数的绝对值不小于它自身
B.若两个有理数的绝对值相等,则这两个数相等
C.若两个有理数的绝对值相等,则这两个数互为相反数
D.﹣a的绝对值等于a
10.计算+++++……+的值为( )
A.
B.
C.
D.
11.下列各式中无论m为何值,一定是正数的是( )
A.|m|
B.|m+1|
C.|m|+1
D.﹣(﹣m)
12.如图,现有3×3的方格,每个小方格内均有不同的数字(1﹣10),要求方格内每一行、每一列以及每一条对角线上的三个数字之和均相等,图中给出了部分数字,则P处对应的数字是( )
A.7
B.5
C.4
D.1
13.计算:1+(﹣2)+(+3)+(﹣4)+(+5)+(﹣6)+…+(+99)+(﹣100)+(+101)的结果是( )
A.0
B.﹣1
C.﹣50
D.51
14.如果|a+b+1|+(b﹣1)2=0,则(a+b)2017的值是( )
A.0
B.1
C.﹣1
D.±1
15.如图,数轴上的六个点满足AB=BC=CD=DE=EF,则在点B、C、D、E对应的数中,最接近﹣10的点是( )
A.点B
B.点C
C.点D
D.点E
16.m是有理数,则m+|m|( )
A.可以是负数
B.不可能是负数
C.一定是正数
D.可是正数也可是负数
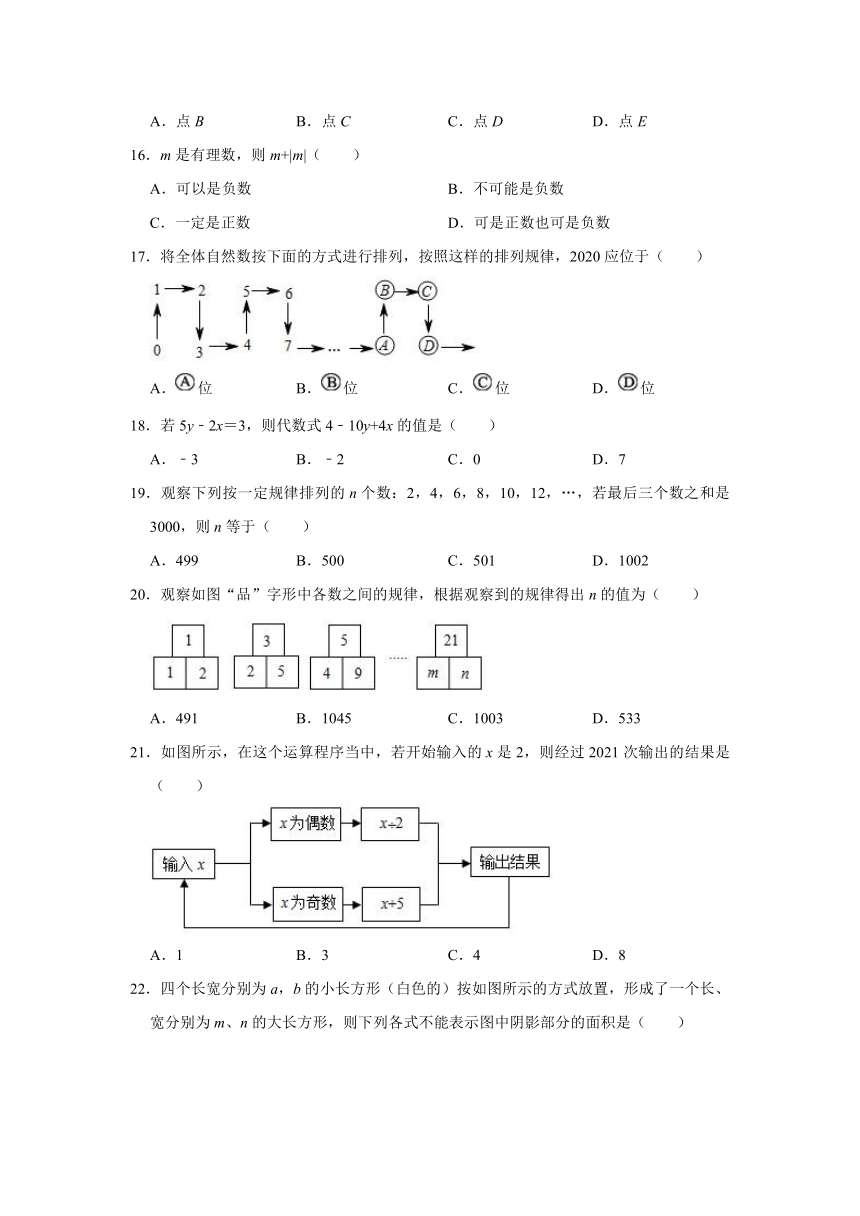
17.将全体自然数按下面的方式进行排列,按照这样的排列规律,2020应位于( )
A.位
B.位
C.位
D.位
18.若5y﹣2x=3,则代数式4﹣10y+4x的值是( )
A.﹣3
B.﹣2
C.0
D.7
19.观察下列按一定规律排列的n个数:2,4,6,8,10,12,…,若最后三个数之和是3000,则n等于( )
A.499
B.500
C.501
D.1002
20.观察如图“品”字形中各数之间的规律,根据观察到的规律得出n的值为( )
A.491
B.1045
C.1003
D.533
21.如图所示,在这个运算程序当中,若开始输入的x是2,则经过2021次输出的结果是( )
A.1
B.3
C.4
D.8
22.四个长宽分别为a,b的小长方形(白色的)按如图所示的方式放置,形成了一个长、宽分别为m、n的大长方形,则下列各式不能表示图中阴影部分的面积是( )
A.mn﹣4ab
B.mn﹣2ab﹣am
C.an+2bn﹣4ab
D.a2﹣2ab﹣am+mn
二.填空题(共7小题)
23.已知a、b互为相反数,c、d互为倒数,那么2a+2b﹣5cd=
.
24.已知有理数a,b,c在数轴上的对应位置如图所示,则|a﹣b|﹣2|b﹣c|﹣|a﹣1|化简后的结果是
.
25.如图,在数轴上点A、B表示的数分别为﹣2、4,若点M从A点出发以每秒5个单位长度的速度沿数轴向右匀速运动,点N从B点出发以每秒4个单位长度的速度沿数轴匀速运动,设点M、N同时出发,运动时间为t秒,经过
秒后,M、N两点间的距离为12个单位长度.
26.已知,|a|=﹣a,=﹣1,|c|=c,化简|a+b|﹣|a﹣c|﹣|b﹣c|=
.
27.一滴墨水洒在一个数轴上,根据图中标出的数值,判断墨迹盖住的整数个数是
.
28.在长为20米、宽为15米的长方形地面上修筑一条宽度为2米的道路(图中阴影部分),余下部分作为耕地,则耕地面积为
平方米.
29.若将正整数按如图所示的规律排列.若用有序数对(a,b)表示第a排,从左至右第b个数.例如(4,3)表示的数是9.则(31,5)表示的数是
.
三.解答题(共10小题)
30.计算下列各题:
(1)(﹣12)﹣5+(﹣17)﹣(﹣13);
(2)(﹣+﹣)×(﹣24);
(3)﹣42﹣(﹣1)2019÷5×+|﹣17+21|.
31.如图,在一条不完整的数轴上从左到右有点A,B,C,其中AB=2BC,设点A,B,C所对应数的和是m.
(1)若点C为原点,BC=1,则点A,B所对应的数分别为
,
,m的值为
;
(2)若点B为原点,AC=6,求m的值.
(3)若原点O到点C的距离为8,且OC=AB,求m的值.
32.结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是
;
数轴上表示﹣3和2两点之间的距离是
;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如数轴上数x与5两点之间的距离等于|x﹣5|,
(2)如果表示数a和﹣2的两点之间的距离是3,那么a=
;若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
33.计算:已知|x|=,|y|=,且x<y<0,求6÷(x﹣y)的值.
34.(1)计算:16÷(﹣2)3﹣(﹣)3×(﹣4)+2.5;
(2)计算:(﹣1)2017+|﹣22+4|﹣(﹣+)×(﹣24)
35.如图,将连续的自然数1至1001按如图的方式排列成一个长方形阵列,用一个正方形框出9个数,要使这个正方形框出的9个数之和分别为:(1)2011;(2)2016.这是否可能?若可能,请写出这9个数中的最小数和最大数;若不可能,试说明理由.
36.观察下列每一列数,按规律填空
(1)﹣7,7,﹣7,7,﹣7,7,
,
,……
(2)2,﹣4,6,﹣8,10,
,
,……
(3)5,0,﹣5,0,5,0,﹣5,0,5,0,
,
,……
(4)在(1)列数中第100个数是
,在(2)列数中第200个数是
,在(3)列数中第199个数是
.
37.国庆期间,王老师计划组织朋友去晋西北游览两日.经了解,现有甲、乙两家旅行社针对组团两日游的游客报价均为每人500元,且提供的服务完全相同.甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按八折收费.假设组团参加甲、乙两家旅行社两日游的人数均为x人.
(1)请列式表示甲、乙两家旅行社收取组团两日游的总费用;
(2)若王老师组团参加两日游的人数共有30人,请你通过计算,在甲、乙两家旅行社中,帮助王老师选择收取总费用较少的一家.
38.每周日,宜春九中(外国语学校)巡逻队乘车沿马路东西方向巡视维护校园安全,星期天早晨从A地出发,最后到达B地,约定向东为正方向,当天的行驶记录如下(单位:千米):
+12,﹣14,+13,﹣10,﹣8,+7,﹣16,+8.
(1)问B地在A地的哪个方向?它们相距多少千米?
(2)若汽车行驶每千米耗油0.2升,求该天共耗油多少升?
39.已知a为整数
(1)|a|能取最
(填“大”或“小”)值是
.此时a=
.
(2)|a|+2能取最
(填“大”或“小”)值是
.此时a=
.
(3)2﹣|a﹣1|能取最
(填“大”或“小”)值是
.此时a=
.
(4)|a﹣1|+|a+2|能取最
(填“大”或“小”)值是
.此时a=
.
参考答案
一.选择题(共22小题)
1.C;
2.B;
3.B;
4.C;
5.A;
6.C;
7.B;
8.C;
9.A;
10.B;
11.C;
12.C;
13.D;
14.C;
15.B;
16.B;
17.A;
18.B;
19.C;
20.B;
21.C;
22.B;
二.填空题(共7小题)
23.﹣5;
24.2c﹣b﹣1;
25.2或18;
26.﹣2c;
27.120;
28.234;
29.470;
三.解答题(共10小题)
30. ;
31.﹣3;﹣1;﹣4;
32.3;5;1或﹣5;
33. ;
34. ;
35. ;
36.﹣7;7;﹣12;14;﹣5;0;7;﹣400;﹣5;
37. ;
38. ;
39.小;0;0;小;2;0;大;2;1;小;3;﹣2或﹣1或0或1;
有理数及其运算
复习练习题
一.选择题(共22小题)
1.下列四个算式:①﹣2﹣3=﹣1;②2﹣|﹣3|=﹣1;③(﹣2)3=﹣6;④﹣2÷=﹣6.其中,正确的算式有( )
A.0个
B.1个
C.2个
D.3个
2.如图,半径为1的圆从表示3的点开始沿着数轴向左滚动一周,圆上的点A与表示3的点重合,滚动一周后到达点B,点B表示的数是( )
A.﹣2π
B.3﹣2π
C.﹣3﹣2π
D.﹣3+2π
3.在数轴上表示有理数a,b,c的点如图所示,若ac<0,b+c<0,则下列式子一定成立的是( )
A.a+c>0
B.a+c<0
C.abc<0
D.|b|<|c|
4.数轴上原点左边有一点A,点A对应着数a,有如下说法:
①﹣a表示的数一定是一个正数.
②若|a|=9时,则a=﹣9.
③在﹣a,,a2,a3中,最大的数值是a2.
④式子|a+|的最小值为2.
其中正确的个数是( )
A.1
B.2
C.3
D.4
5.如果a,b互为相反数,x,y互为倒数,m的倒数等于它本身,则6(a+b)+m2﹣3xy的值是( )
A.﹣2
B.﹣1
C.0
D.1
6.x是数轴上任意一点表示的数,若|x﹣3|+|x+2|的值最小,则x的取值范围是( )
A.x≥3
B.x≤﹣2
C.﹣2≤x≤3
D.﹣2<x<3
7.当|a|=5,|b|=7,且|a+b|=a+b,则a﹣b的值为( )
A.﹣12
B.﹣2或﹣12
C.2
D.﹣2
8.如果a+b+c=0,且|a|>|b|>|c|.则下列说法中可能成立的是( )
A.b为正数,c为负数
B.c为正数,b为负数
C.c为正数,a为负数
D.c为负数,a为负数
9.下列说法中,正确的是( )
A.一个有理数的绝对值不小于它自身
B.若两个有理数的绝对值相等,则这两个数相等
C.若两个有理数的绝对值相等,则这两个数互为相反数
D.﹣a的绝对值等于a
10.计算+++++……+的值为( )
A.
B.
C.
D.
11.下列各式中无论m为何值,一定是正数的是( )
A.|m|
B.|m+1|
C.|m|+1
D.﹣(﹣m)
12.如图,现有3×3的方格,每个小方格内均有不同的数字(1﹣10),要求方格内每一行、每一列以及每一条对角线上的三个数字之和均相等,图中给出了部分数字,则P处对应的数字是( )
A.7
B.5
C.4
D.1
13.计算:1+(﹣2)+(+3)+(﹣4)+(+5)+(﹣6)+…+(+99)+(﹣100)+(+101)的结果是( )
A.0
B.﹣1
C.﹣50
D.51
14.如果|a+b+1|+(b﹣1)2=0,则(a+b)2017的值是( )
A.0
B.1
C.﹣1
D.±1
15.如图,数轴上的六个点满足AB=BC=CD=DE=EF,则在点B、C、D、E对应的数中,最接近﹣10的点是( )
A.点B
B.点C
C.点D
D.点E
16.m是有理数,则m+|m|( )
A.可以是负数
B.不可能是负数
C.一定是正数
D.可是正数也可是负数
17.将全体自然数按下面的方式进行排列,按照这样的排列规律,2020应位于( )
A.位
B.位
C.位
D.位
18.若5y﹣2x=3,则代数式4﹣10y+4x的值是( )
A.﹣3
B.﹣2
C.0
D.7
19.观察下列按一定规律排列的n个数:2,4,6,8,10,12,…,若最后三个数之和是3000,则n等于( )
A.499
B.500
C.501
D.1002
20.观察如图“品”字形中各数之间的规律,根据观察到的规律得出n的值为( )
A.491
B.1045
C.1003
D.533
21.如图所示,在这个运算程序当中,若开始输入的x是2,则经过2021次输出的结果是( )
A.1
B.3
C.4
D.8
22.四个长宽分别为a,b的小长方形(白色的)按如图所示的方式放置,形成了一个长、宽分别为m、n的大长方形,则下列各式不能表示图中阴影部分的面积是( )
A.mn﹣4ab
B.mn﹣2ab﹣am
C.an+2bn﹣4ab
D.a2﹣2ab﹣am+mn
二.填空题(共7小题)
23.已知a、b互为相反数,c、d互为倒数,那么2a+2b﹣5cd=
.
24.已知有理数a,b,c在数轴上的对应位置如图所示,则|a﹣b|﹣2|b﹣c|﹣|a﹣1|化简后的结果是
.
25.如图,在数轴上点A、B表示的数分别为﹣2、4,若点M从A点出发以每秒5个单位长度的速度沿数轴向右匀速运动,点N从B点出发以每秒4个单位长度的速度沿数轴匀速运动,设点M、N同时出发,运动时间为t秒,经过
秒后,M、N两点间的距离为12个单位长度.
26.已知,|a|=﹣a,=﹣1,|c|=c,化简|a+b|﹣|a﹣c|﹣|b﹣c|=
.
27.一滴墨水洒在一个数轴上,根据图中标出的数值,判断墨迹盖住的整数个数是
.
28.在长为20米、宽为15米的长方形地面上修筑一条宽度为2米的道路(图中阴影部分),余下部分作为耕地,则耕地面积为
平方米.
29.若将正整数按如图所示的规律排列.若用有序数对(a,b)表示第a排,从左至右第b个数.例如(4,3)表示的数是9.则(31,5)表示的数是
.
三.解答题(共10小题)
30.计算下列各题:
(1)(﹣12)﹣5+(﹣17)﹣(﹣13);
(2)(﹣+﹣)×(﹣24);
(3)﹣42﹣(﹣1)2019÷5×+|﹣17+21|.
31.如图,在一条不完整的数轴上从左到右有点A,B,C,其中AB=2BC,设点A,B,C所对应数的和是m.
(1)若点C为原点,BC=1,则点A,B所对应的数分别为
,
,m的值为
;
(2)若点B为原点,AC=6,求m的值.
(3)若原点O到点C的距离为8,且OC=AB,求m的值.
32.结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是
;
数轴上表示﹣3和2两点之间的距离是
;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如数轴上数x与5两点之间的距离等于|x﹣5|,
(2)如果表示数a和﹣2的两点之间的距离是3,那么a=
;若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
33.计算:已知|x|=,|y|=,且x<y<0,求6÷(x﹣y)的值.
34.(1)计算:16÷(﹣2)3﹣(﹣)3×(﹣4)+2.5;
(2)计算:(﹣1)2017+|﹣22+4|﹣(﹣+)×(﹣24)
35.如图,将连续的自然数1至1001按如图的方式排列成一个长方形阵列,用一个正方形框出9个数,要使这个正方形框出的9个数之和分别为:(1)2011;(2)2016.这是否可能?若可能,请写出这9个数中的最小数和最大数;若不可能,试说明理由.
36.观察下列每一列数,按规律填空
(1)﹣7,7,﹣7,7,﹣7,7,
,
,……
(2)2,﹣4,6,﹣8,10,
,
,……
(3)5,0,﹣5,0,5,0,﹣5,0,5,0,
,
,……
(4)在(1)列数中第100个数是
,在(2)列数中第200个数是
,在(3)列数中第199个数是
.
37.国庆期间,王老师计划组织朋友去晋西北游览两日.经了解,现有甲、乙两家旅行社针对组团两日游的游客报价均为每人500元,且提供的服务完全相同.甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按八折收费.假设组团参加甲、乙两家旅行社两日游的人数均为x人.
(1)请列式表示甲、乙两家旅行社收取组团两日游的总费用;
(2)若王老师组团参加两日游的人数共有30人,请你通过计算,在甲、乙两家旅行社中,帮助王老师选择收取总费用较少的一家.
38.每周日,宜春九中(外国语学校)巡逻队乘车沿马路东西方向巡视维护校园安全,星期天早晨从A地出发,最后到达B地,约定向东为正方向,当天的行驶记录如下(单位:千米):
+12,﹣14,+13,﹣10,﹣8,+7,﹣16,+8.
(1)问B地在A地的哪个方向?它们相距多少千米?
(2)若汽车行驶每千米耗油0.2升,求该天共耗油多少升?
39.已知a为整数
(1)|a|能取最
(填“大”或“小”)值是
.此时a=
.
(2)|a|+2能取最
(填“大”或“小”)值是
.此时a=
.
(3)2﹣|a﹣1|能取最
(填“大”或“小”)值是
.此时a=
.
(4)|a﹣1|+|a+2|能取最
(填“大”或“小”)值是
.此时a=
.
参考答案
一.选择题(共22小题)
1.C;
2.B;
3.B;
4.C;
5.A;
6.C;
7.B;
8.C;
9.A;
10.B;
11.C;
12.C;
13.D;
14.C;
15.B;
16.B;
17.A;
18.B;
19.C;
20.B;
21.C;
22.B;
二.填空题(共7小题)
23.﹣5;
24.2c﹣b﹣1;
25.2或18;
26.﹣2c;
27.120;
28.234;
29.470;
三.解答题(共10小题)
30. ;
31.﹣3;﹣1;﹣4;
32.3;5;1或﹣5;
33. ;
34. ;
35. ;
36.﹣7;7;﹣12;14;﹣5;0;7;﹣400;﹣5;
37. ;
38. ;
39.小;0;0;小;2;0;大;2;1;小;3;﹣2或﹣1或0或1;
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
