14.2 三角形全等的判定 第1课时 全等三角形的判定定理-SAS 课件(共30张)
文档属性
| 名称 | 14.2 三角形全等的判定 第1课时 全等三角形的判定定理-SAS 课件(共30张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 10:31:52 | ||
图片预览






文档简介
(共30张PPT)
第1课时
全等三角形的判定定理
——SAS
14.2
三角形全等的判定
沪科版·八年级数学上册
教学课件
学习目标
【知识与技能】
理解判定两个三角形全等的方法之一——“边角边”定理,深化证明思维.
【过程与方法】
经历探究“边角边”判定两个三角形全等的定理的过程,能进行有条理的思索.
【情感与态度】
培养严谨的分析能力,体会几何学的应用价值.
【教学重点】
重点是运用“边角边”的判定定理解决实际问题.
【教学难点】
难点是如何寻找适合“边角边”的判定定理来证明全等的两个三角形.
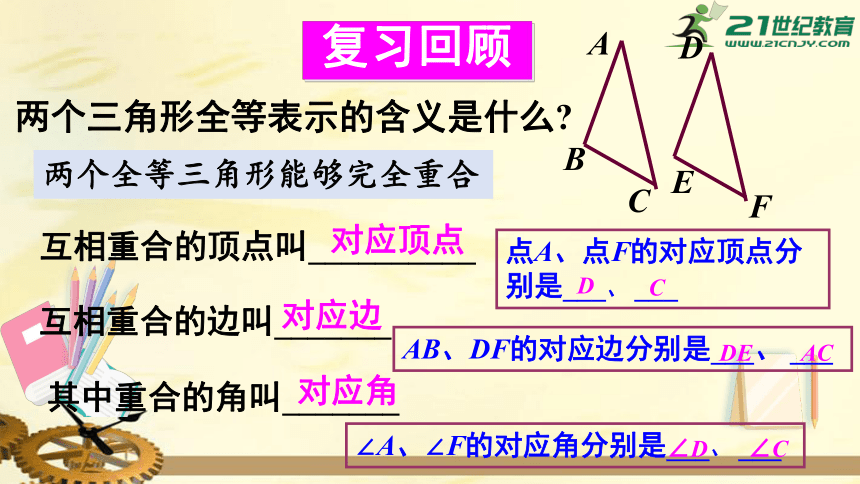
两个三角形全等表示的含义是什么?
两个全等三角形能够完全重合
互相重合的顶点叫__________
互相重合的边叫_______
其中重合的角叫_______
对应顶点
对应角
对应边
点A、点F的对应顶点分别是___、
___
AB、DF的对应边分别是___、
___
∠A、∠F的对应角分别是___、
___
D
C
DE
AC
∠D
∠C
A
B
C
D
E
F
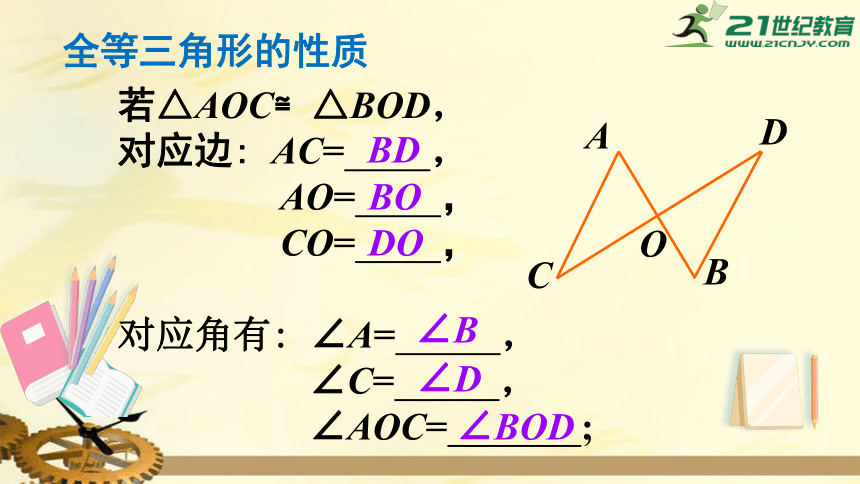
复习回顾
若△AOC≌△BOD,
对应边:
AC=
,
AO=
,
CO=
,
对应角有:
∠A=
,
∠C=
,
∠AOC=
;
A
B
O
C
D
全等三角形的性质
BD
BO
DO
∠B
∠D
∠BOD
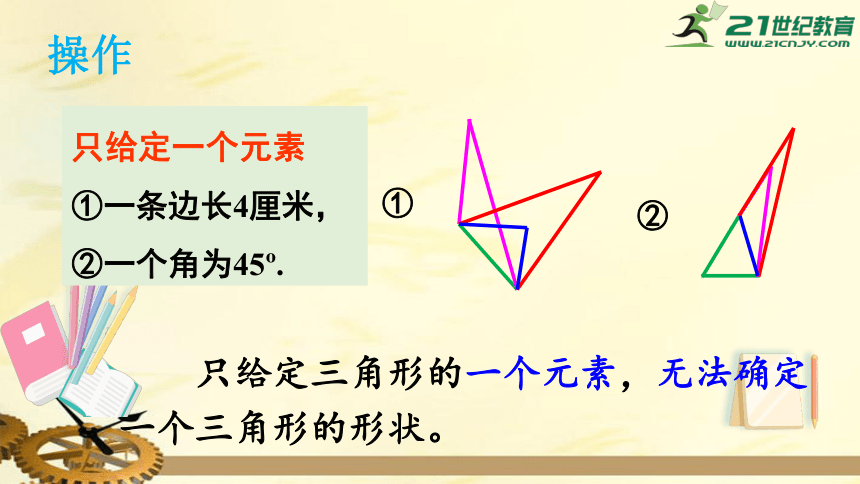
三角形有六个基本元素(三边三角),要确定一个三角形的形状,需要几个元素呢?
探索新知
不妨试一试
只给定三角形的一个或两个元素,能够确定一个三角形的形状吗?通过画图,说明你的判断。
只给定一个元素
①一条边长4厘米,
②一个角为45?.
只给定两个元素
①两条边分别长4厘米、5厘米,
②一条边长为4厘米,一个角为45?,
③
两个角分别为45?、60?.
只给定一个元素
①一条边长4厘米,
②一个角为45?.
操作
①
②
只给定三角形的一个元素,无法确定一个三角形的形状。
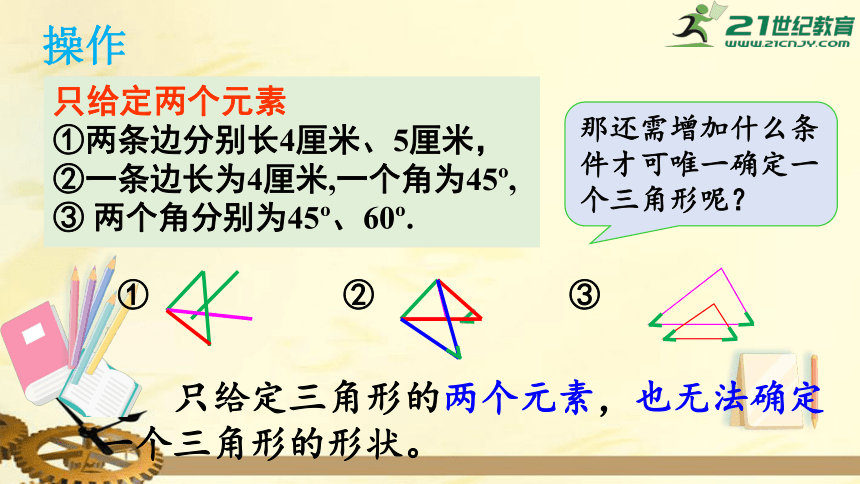
只给定两个元素
①两条边分别长4厘米、5厘米,
②一条边长为4厘米,一个角为45?,
③
两个角分别为45?、60?.
操作
①
②
③
只给定三角形的两个元素,也无法确定一个三角形的形状。
那还需增加什么条件才可唯一确定一个三角形呢?
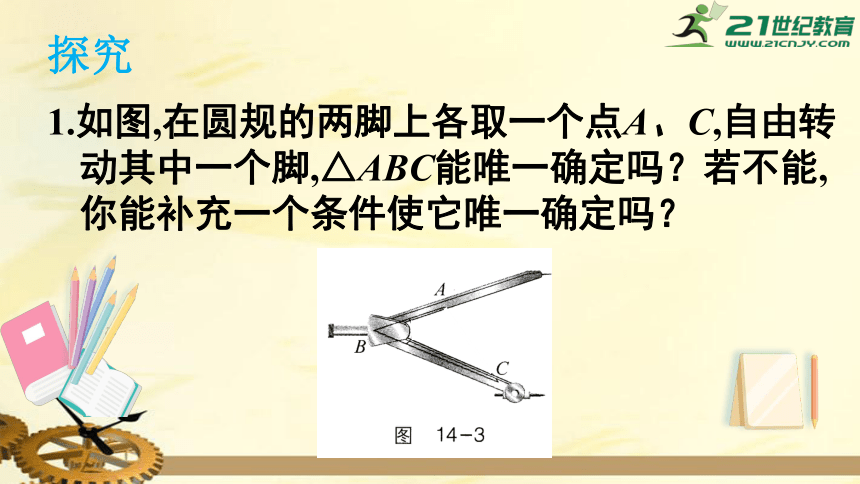
1.如图,在圆规的两脚上各取一个点A、C,自由转动其中一个脚,△ABC能唯一确定吗?若不能,你能补充一个条件使它唯一确定吗?
探究
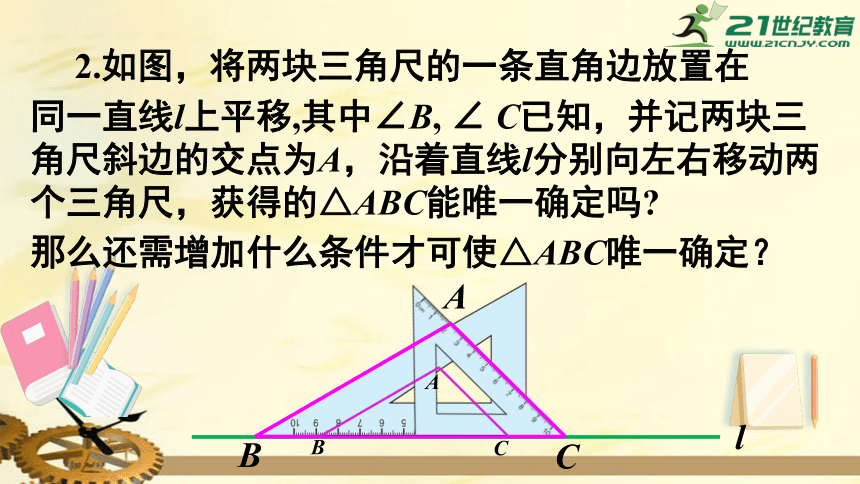
2.如图,将两块三角尺的一条直角边放置在
同一直线l上平移,其中∠B,
∠
C已知,并记两块三角尺斜边的交点为A,沿着直线l分别向左右移动两个三角尺,获得的△ABC能唯一确定吗?
那么还需增加什么条件才可使△ABC唯一确定?
A
B
C
l
A
B
C
归纳总结,继续探究
确定一个三角形的形状,大小需要三个元素,确定三角形形状,大小的条件能否作为判断三角形全等的条件呢?
先任意画出一个△ABC,再画出一个△A′B′C′使A′B′=AB,B′C′=BC,∠B=∠B′。
画一画
画法:
2.
在射线B′M上截取B′A′=
BA
3.
在射线B′N上截取B′C′=BC
1.
作∠MB′N=
∠B
4.
连接A′C′
A
B
C
A′
B′
C′
M
N
△ABC
与△A′B′C′能互相重合吗?
两边及其夹角分别相等的两个三角形全等.简记为“边角边”或“SAS”.
基本事实:
三角形全等判定方法1
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边及其夹角分别相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
角写在中间
4
4
1.如图,在下列三角形中,哪两个三角形全等?
4
4
5
5
30°
30°
4
4
30°
4
6
40°
5
6
40°
40°
①
③
②
⑥
⑤
④
练一练
2.在下列图中找出全等三角形,并把它们用直线连起来.
Ⅰ
?
30?
8
cm
9
cm
Ⅵ
?
30?
8
cm
8
cm
Ⅳ
Ⅳ
8
cm
5
cm
Ⅴ
30?
8
cm
?
5
cm
Ⅷ
8
cm
5
cm
?
30?
8
cm
9
cm
Ⅶ
Ⅲ
?
30?
8
cm
8
cm
Ⅲ
8
cm
Ⅱ
5
cm
30?
已知:如图,AD∥BC,AD=CB
求证:△ADC≌△CBA.
AD=CB(已知)
∠1=∠2(已证)
AC=CA
(公共边)
例1:
证明:∵AD∥BC
∴∠1=∠2(两直线平行,内错角相等)
在△DAC和△CBA中
D
C
1
A
B
2
∴△ADC≌△CBA(SAS)
典例解析
选择:下列能证明两个三角形全等的是(
)
A
B
C
D
E
F
(1)AB=DE
AC=DF
∠B=∠E
(2)
AB=DE
AC=DF
∠A=∠E
(3)
AB=DE
AC=DF
∠A=∠D
√
在人工湖的岸边有A、B两点,难以直接量出A、B两点间的距离。你能设计一种量出A、B两点之间距离的方案吗?
例2:
解:在岸上取可以直接到达A,B的一点C,连接AC,延长AC到点A′,使A′C=AC;连接BC,并延长BC到点B′,使B′C=BC.连接A′
B′,量出的长度,就是AB两点间距离.
A′
B′
理由:在△ABC与△A′B′C中,
∵
AC=A′C
∠ACB=
∠
A′C
B′,(对顶角相等)
BC=B′C
∴△ABC≌△A′B′C.(SAS)
∴A′B′=AB.(全等三角形对应边相等)
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?动手画一画,你发现了什么?
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其一边所对的角相等,两个三角形不一定全等
注:这个角一定要是这两边所夹的角
1.如图,已知AB=AC,AD=AE.
求证:∠B=∠C.
B
C
D
E
A
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形对应角相等)
随堂练习
AB=AC(已知)
∠A=∠A(公共角)
AD=AE
(已知)
2.已知:如图,
AC和BD相交于点O,OA=OC,OB=OD.
求证:DC∥AB.
证明:
OA=OC(已知)
∠AOB
=∠COD
(对顶角相等)
OB=OD
(已知)
∵
∴△COD≌△AOB(SAS)
∴∠C=∠A(全等三角形对应角相等)
∴
DC∥AB
(内错角相等的两条直线平行)
1
2
3.已知:如图,AB=AC,AD=AE,∠1=∠2.
求证:△ABD≌△ACE.
1
2
证明:
∵∠1=∠2(已知)
∴∠1+∠BAE
=
∠2+∠BAE(等式的性质)
即
∠BAD=
∠CAE
在△CAE和△BAD
中
AC=AB(已知)
∠CAE=∠BAD(已证)
AE=AD
∴△ABD≌△ACE(SAS)
完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第1课时
全等三角形的判定定理
——SAS
14.2
三角形全等的判定
沪科版·八年级数学上册
教学课件
学习目标
【知识与技能】
理解判定两个三角形全等的方法之一——“边角边”定理,深化证明思维.
【过程与方法】
经历探究“边角边”判定两个三角形全等的定理的过程,能进行有条理的思索.
【情感与态度】
培养严谨的分析能力,体会几何学的应用价值.
【教学重点】
重点是运用“边角边”的判定定理解决实际问题.
【教学难点】
难点是如何寻找适合“边角边”的判定定理来证明全等的两个三角形.
两个三角形全等表示的含义是什么?
两个全等三角形能够完全重合
互相重合的顶点叫__________
互相重合的边叫_______
其中重合的角叫_______
对应顶点
对应角
对应边
点A、点F的对应顶点分别是___、
___
AB、DF的对应边分别是___、
___
∠A、∠F的对应角分别是___、
___
D
C
DE
AC
∠D
∠C
A
B
C
D
E
F
复习回顾
若△AOC≌△BOD,
对应边:
AC=
,
AO=
,
CO=
,
对应角有:
∠A=
,
∠C=
,
∠AOC=
;
A
B
O
C
D
全等三角形的性质
BD
BO
DO
∠B
∠D
∠BOD
三角形有六个基本元素(三边三角),要确定一个三角形的形状,需要几个元素呢?
探索新知
不妨试一试
只给定三角形的一个或两个元素,能够确定一个三角形的形状吗?通过画图,说明你的判断。
只给定一个元素
①一条边长4厘米,
②一个角为45?.
只给定两个元素
①两条边分别长4厘米、5厘米,
②一条边长为4厘米,一个角为45?,
③
两个角分别为45?、60?.
只给定一个元素
①一条边长4厘米,
②一个角为45?.
操作
①
②
只给定三角形的一个元素,无法确定一个三角形的形状。
只给定两个元素
①两条边分别长4厘米、5厘米,
②一条边长为4厘米,一个角为45?,
③
两个角分别为45?、60?.
操作
①
②
③
只给定三角形的两个元素,也无法确定一个三角形的形状。
那还需增加什么条件才可唯一确定一个三角形呢?
1.如图,在圆规的两脚上各取一个点A、C,自由转动其中一个脚,△ABC能唯一确定吗?若不能,你能补充一个条件使它唯一确定吗?
探究
2.如图,将两块三角尺的一条直角边放置在
同一直线l上平移,其中∠B,
∠
C已知,并记两块三角尺斜边的交点为A,沿着直线l分别向左右移动两个三角尺,获得的△ABC能唯一确定吗?
那么还需增加什么条件才可使△ABC唯一确定?
A
B
C
l
A
B
C
归纳总结,继续探究
确定一个三角形的形状,大小需要三个元素,确定三角形形状,大小的条件能否作为判断三角形全等的条件呢?
先任意画出一个△ABC,再画出一个△A′B′C′使A′B′=AB,B′C′=BC,∠B=∠B′。
画一画
画法:
2.
在射线B′M上截取B′A′=
BA
3.
在射线B′N上截取B′C′=BC
1.
作∠MB′N=
∠B
4.
连接A′C′
A
B
C
A′
B′
C′
M
N
△ABC
与△A′B′C′能互相重合吗?
两边及其夹角分别相等的两个三角形全等.简记为“边角边”或“SAS”.
基本事实:
三角形全等判定方法1
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边及其夹角分别相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
角写在中间
4
4
1.如图,在下列三角形中,哪两个三角形全等?
4
4
5
5
30°
30°
4
4
30°
4
6
40°
5
6
40°
40°
①
③
②
⑥
⑤
④
练一练
2.在下列图中找出全等三角形,并把它们用直线连起来.
Ⅰ
?
30?
8
cm
9
cm
Ⅵ
?
30?
8
cm
8
cm
Ⅳ
Ⅳ
8
cm
5
cm
Ⅴ
30?
8
cm
?
5
cm
Ⅷ
8
cm
5
cm
?
30?
8
cm
9
cm
Ⅶ
Ⅲ
?
30?
8
cm
8
cm
Ⅲ
8
cm
Ⅱ
5
cm
30?
已知:如图,AD∥BC,AD=CB
求证:△ADC≌△CBA.
AD=CB(已知)
∠1=∠2(已证)
AC=CA
(公共边)
例1:
证明:∵AD∥BC
∴∠1=∠2(两直线平行,内错角相等)
在△DAC和△CBA中
D
C
1
A
B
2
∴△ADC≌△CBA(SAS)
典例解析
选择:下列能证明两个三角形全等的是(
)
A
B
C
D
E
F
(1)AB=DE
AC=DF
∠B=∠E
(2)
AB=DE
AC=DF
∠A=∠E
(3)
AB=DE
AC=DF
∠A=∠D
√
在人工湖的岸边有A、B两点,难以直接量出A、B两点间的距离。你能设计一种量出A、B两点之间距离的方案吗?
例2:
解:在岸上取可以直接到达A,B的一点C,连接AC,延长AC到点A′,使A′C=AC;连接BC,并延长BC到点B′,使B′C=BC.连接A′
B′,量出的长度,就是AB两点间距离.
A′
B′
理由:在△ABC与△A′B′C中,
∵
AC=A′C
∠ACB=
∠
A′C
B′,(对顶角相等)
BC=B′C
∴△ABC≌△A′B′C.(SAS)
∴A′B′=AB.(全等三角形对应边相等)
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?动手画一画,你发现了什么?
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其一边所对的角相等,两个三角形不一定全等
注:这个角一定要是这两边所夹的角
1.如图,已知AB=AC,AD=AE.
求证:∠B=∠C.
B
C
D
E
A
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形对应角相等)
随堂练习
AB=AC(已知)
∠A=∠A(公共角)
AD=AE
(已知)
2.已知:如图,
AC和BD相交于点O,OA=OC,OB=OD.
求证:DC∥AB.
证明:
OA=OC(已知)
∠AOB
=∠COD
(对顶角相等)
OB=OD
(已知)
∵
∴△COD≌△AOB(SAS)
∴∠C=∠A(全等三角形对应角相等)
∴
DC∥AB
(内错角相等的两条直线平行)
1
2
3.已知:如图,AB=AC,AD=AE,∠1=∠2.
求证:△ABD≌△ACE.
1
2
证明:
∵∠1=∠2(已知)
∴∠1+∠BAE
=
∠2+∠BAE(等式的性质)
即
∠BAD=
∠CAE
在△CAE和△BAD
中
AC=AB(已知)
∠CAE=∠BAD(已证)
AE=AD
∴△ABD≌△ACE(SAS)
完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
