14.2 三角形全等的判定 第2课时 全等三角形的判定定理-ASA 课件(共20张PPT)
文档属性
| 名称 | 14.2 三角形全等的判定 第2课时 全等三角形的判定定理-ASA 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 09:11:29 | ||
图片预览



文档简介
(共20张PPT)
第2课时
全等三角形的判定定理
——ASA
沪科版·八年级数学上册
教学课件
14.2
三角形全等的判定
学习目标
【知识与技能】
理解“角边角”判定两个三角形全等的方法.
【过程与方法】
经历探究“角边角”判定两个三角形全等的过程,能进行有条理的思索.
【情感与态度】
培养严谨的表述能力,体会几何中逻辑推理的应用价值.
【教学重点】
重点是学会运用“角边角”判定两个三角形全等的方法.
【教学难点】
难点是如何进行推理分析.
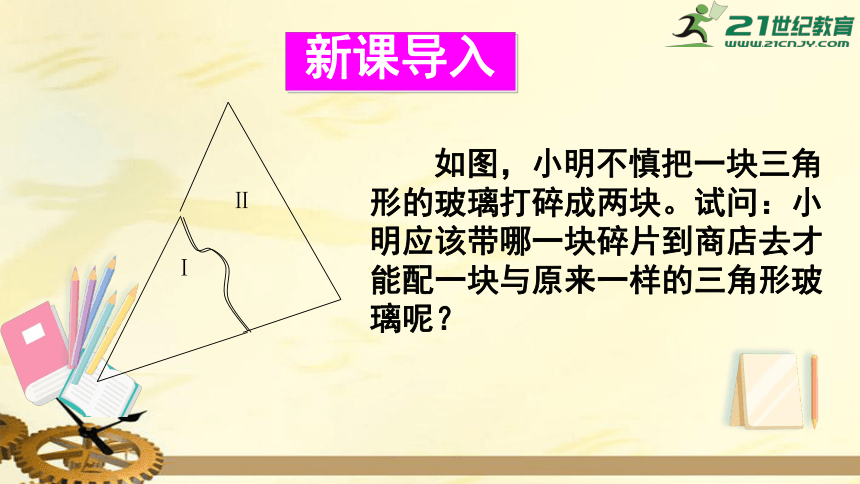
如图,小明不慎把一块三角形的玻璃打碎成两块。试问:小明应该带哪一块碎片到商店去才能配一块与原来一样的三角形玻璃呢?
Ⅰ
Ⅱ
新课导入
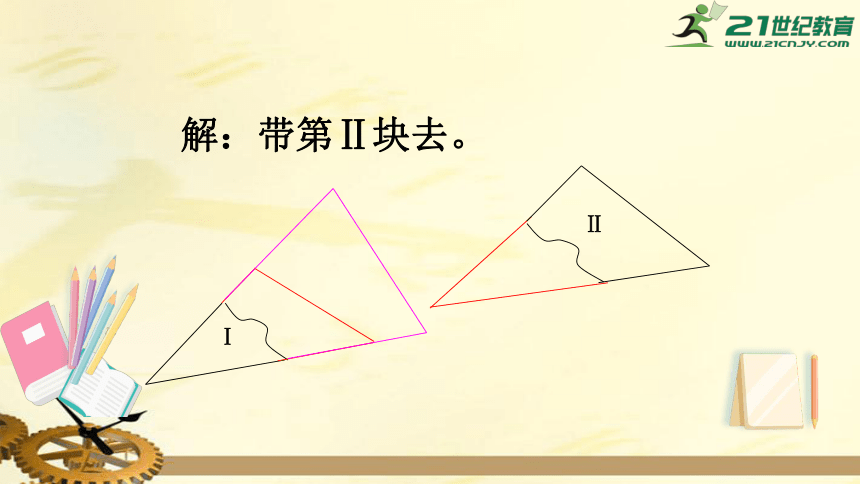
Ⅰ
Ⅱ
解:带第Ⅱ块去。
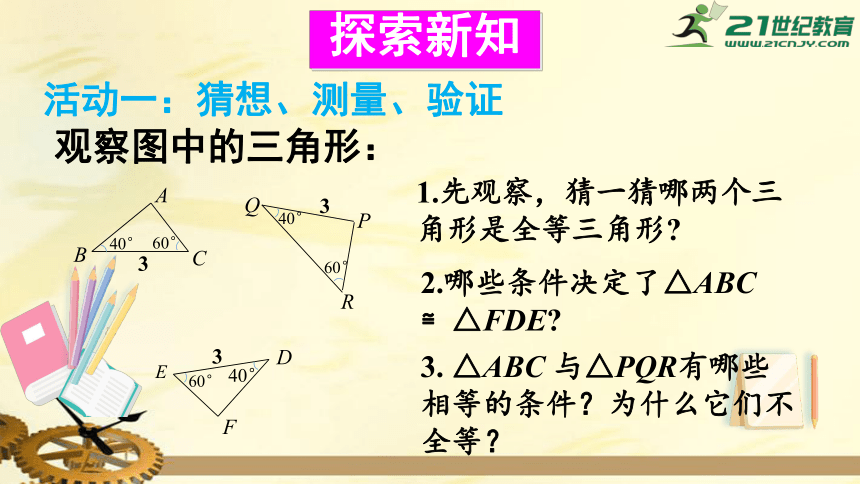
活动一:猜想、测量、验证
观察图中的三角形:
1.先观察,猜一猜哪两个三角形是全等三角形?
2.哪些条件决定了△ABC
≌△FDE?
3.
△ABC
与△PQR有哪些相等的条件?为什么它们不全等?
探索新知
A
B
3
60°
40°
C
3
40°
60°
P
R
Q
60°
40°
D
F
E
3
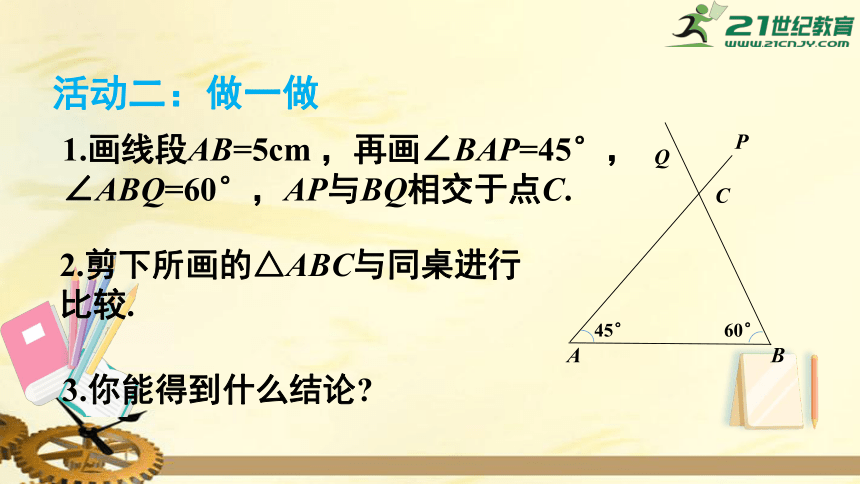
活动二:做一做
1.画线段AB=5cm
,再画∠BAP=45°,∠ABQ=60°,AP与BQ相交于点C.
2.剪下所画的△ABC与同桌进行比较.
3.你能得到什么结论?
A
B
P
Q
C
45°
60°
全等三角形判定方法2:
两角及其夹分别相等的两个三角形全等.简写成“角边角”或“ASA”.
一定要注意
“两角夹边”的顺序!
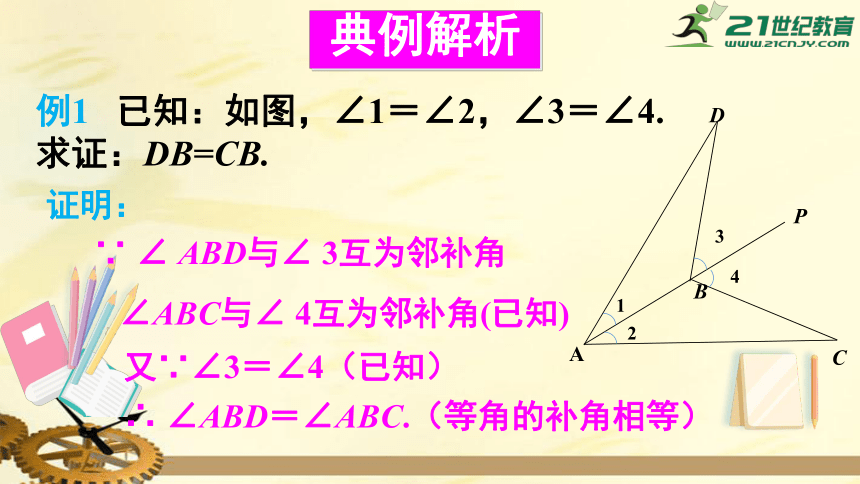
例1
已知:如图,∠1=∠2,∠3=∠4.
求证:DB=CB.
D
A
C
P
B
证明:
∵
∠
ABD与∠
3互为邻补角
∠ABC与∠
4互为邻补角(已知)
又∵∠3=∠4(已知)
∴
∠ABD=∠ABC.(等角的补角相等)
典例解析
1
2
3
4
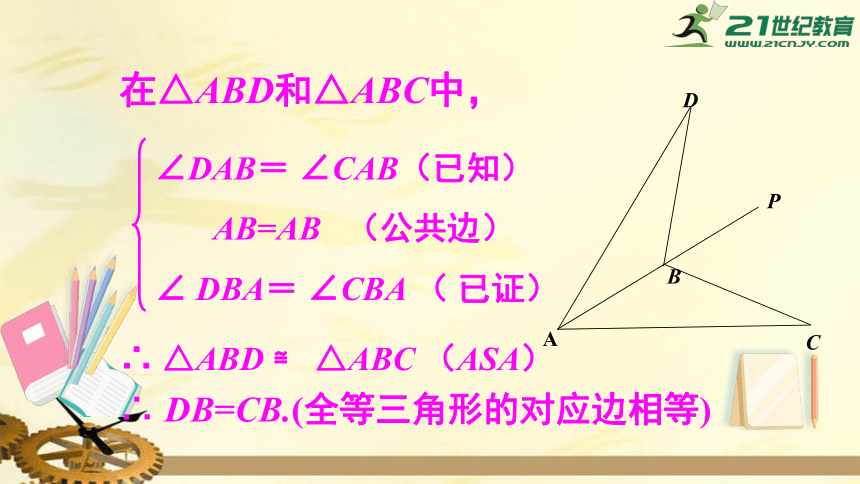
在△ABD和△ABC中,
∠DAB=
∠CAB(已知)
AB=AB
(公共边)
∠
DBA=
∠CBA
(
已证)
∴
△ABD
≌
△ABC
(ASA)
D
A
C
P
B
∴
DB=CB.(全等三角形的对应边相等)
已知:如图,要测量河两岸相对的两点A、B之间的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再过点D作BF的垂线DE.使点A、C、E在一条直线上,这时测得DE的长等于AB的长,请说明道理.
------------------------------------------------------------------------------------------------------------------------------------------------------------
A
B
C
D
E
F
例2
已知AB⊥BD,ED
⊥
BD,且AE交BD于C,BC=CD
分析:
1.寻求已知条件:
2.转化为判定的条件:
∠
ABC=∠EDC=90°
(垂直定义)
BC=DC(已知条件)
∠
ACB=∠
ECD
(对顶角相等)
3.得出结论:
证明:
∵
AB⊥BD,ED
⊥
BD(已知)
∴∠
ABC=∠EDC=90°(垂直的定义)
∠
ABC=∠EDC
(已证)
BC=DC(已知)
∠
ACB=∠
ECD
(对顶角相等)
在△ABC和△EDC中,
∴△ABC≌△EDC(ASA)
∴AB=ED(全等三角形的对应边相等)
随堂练习
1.已知:如图,∠1=∠2,∠ABC=∠DCB.求证:△ABC≌△DCB.
A
B
C
D
1
2
△ABC≌△DCB(ASA)
证明:
∠1=∠2(已知)
BC=BC(公共边)
∠ABC=∠DCB(已知)
2.已知:如图,∠BAD=∠CAD,AD⊥BC,点D为垂足.求证:△ABD≌△ACD.
A
B
C
D
△ABD≌△ACD
(ASA)
证明:
∠
BAD
=∠
CAD
(已知)
AD=AD(公共边)
∴∠BDA=∠CDA
(已证)
∵AD⊥BC,
∴∠BDA=∠CDA=90°
3.两个直角三角形中,斜边和一个锐角分别对应相等.求证这两个三角形全等.
A
B
C
E
F
D
证明:如图
已知:∠ABC=∠DEF=90°
AC=DF
∠A=∠D
求证:△ABC≌
△
DEF
A
B
C
E
F
D
∵∠ABC=∠DEF=90°,∠A=∠D
∴
∠C=∠F(三角形内角和为180°)
∴
∠A=∠D(已知)
AC=DF(已知)
∠C=∠F(已证)
∴△ABC≌
△
DEF
4.如图OP是∠
MON的角平分线,
C是OP上的一点,CA⊥
OM,
CB⊥ON,垂足分别为A、B,△
AOC
≌
△
BOC吗
?为什么?
O
B
N
P
M
C
┎
┛
A
解:
△
AOC
≌
△
BOC.
∵
CA
⊥
OM,
CB⊥ON.
∴
∠
CAO=
∠
CBO=90
°
.
∵
OP是∠
MON的平分线,
∴
∠
AOC=
∠
BOC
.
又∵
OC=
OC
.
∴
△
AOC
≌
△
BOC
.(ASA)
∴
∠
OCA=
∠
OCB
.
完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第2课时
全等三角形的判定定理
——ASA
沪科版·八年级数学上册
教学课件
14.2
三角形全等的判定
学习目标
【知识与技能】
理解“角边角”判定两个三角形全等的方法.
【过程与方法】
经历探究“角边角”判定两个三角形全等的过程,能进行有条理的思索.
【情感与态度】
培养严谨的表述能力,体会几何中逻辑推理的应用价值.
【教学重点】
重点是学会运用“角边角”判定两个三角形全等的方法.
【教学难点】
难点是如何进行推理分析.
如图,小明不慎把一块三角形的玻璃打碎成两块。试问:小明应该带哪一块碎片到商店去才能配一块与原来一样的三角形玻璃呢?
Ⅰ
Ⅱ
新课导入
Ⅰ
Ⅱ
解:带第Ⅱ块去。
活动一:猜想、测量、验证
观察图中的三角形:
1.先观察,猜一猜哪两个三角形是全等三角形?
2.哪些条件决定了△ABC
≌△FDE?
3.
△ABC
与△PQR有哪些相等的条件?为什么它们不全等?
探索新知
A
B
3
60°
40°
C
3
40°
60°
P
R
Q
60°
40°
D
F
E
3
活动二:做一做
1.画线段AB=5cm
,再画∠BAP=45°,∠ABQ=60°,AP与BQ相交于点C.
2.剪下所画的△ABC与同桌进行比较.
3.你能得到什么结论?
A
B
P
Q
C
45°
60°
全等三角形判定方法2:
两角及其夹分别相等的两个三角形全等.简写成“角边角”或“ASA”.
一定要注意
“两角夹边”的顺序!
例1
已知:如图,∠1=∠2,∠3=∠4.
求证:DB=CB.
D
A
C
P
B
证明:
∵
∠
ABD与∠
3互为邻补角
∠ABC与∠
4互为邻补角(已知)
又∵∠3=∠4(已知)
∴
∠ABD=∠ABC.(等角的补角相等)
典例解析
1
2
3
4
在△ABD和△ABC中,
∠DAB=
∠CAB(已知)
AB=AB
(公共边)
∠
DBA=
∠CBA
(
已证)
∴
△ABD
≌
△ABC
(ASA)
D
A
C
P
B
∴
DB=CB.(全等三角形的对应边相等)
已知:如图,要测量河两岸相对的两点A、B之间的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再过点D作BF的垂线DE.使点A、C、E在一条直线上,这时测得DE的长等于AB的长,请说明道理.
------------------------------------------------------------------------------------------------------------------------------------------------------------
A
B
C
D
E
F
例2
已知AB⊥BD,ED
⊥
BD,且AE交BD于C,BC=CD
分析:
1.寻求已知条件:
2.转化为判定的条件:
∠
ABC=∠EDC=90°
(垂直定义)
BC=DC(已知条件)
∠
ACB=∠
ECD
(对顶角相等)
3.得出结论:
证明:
∵
AB⊥BD,ED
⊥
BD(已知)
∴∠
ABC=∠EDC=90°(垂直的定义)
∠
ABC=∠EDC
(已证)
BC=DC(已知)
∠
ACB=∠
ECD
(对顶角相等)
在△ABC和△EDC中,
∴△ABC≌△EDC(ASA)
∴AB=ED(全等三角形的对应边相等)
随堂练习
1.已知:如图,∠1=∠2,∠ABC=∠DCB.求证:△ABC≌△DCB.
A
B
C
D
1
2
△ABC≌△DCB(ASA)
证明:
∠1=∠2(已知)
BC=BC(公共边)
∠ABC=∠DCB(已知)
2.已知:如图,∠BAD=∠CAD,AD⊥BC,点D为垂足.求证:△ABD≌△ACD.
A
B
C
D
△ABD≌△ACD
(ASA)
证明:
∠
BAD
=∠
CAD
(已知)
AD=AD(公共边)
∴∠BDA=∠CDA
(已证)
∵AD⊥BC,
∴∠BDA=∠CDA=90°
3.两个直角三角形中,斜边和一个锐角分别对应相等.求证这两个三角形全等.
A
B
C
E
F
D
证明:如图
已知:∠ABC=∠DEF=90°
AC=DF
∠A=∠D
求证:△ABC≌
△
DEF
A
B
C
E
F
D
∵∠ABC=∠DEF=90°,∠A=∠D
∴
∠C=∠F(三角形内角和为180°)
∴
∠A=∠D(已知)
AC=DF(已知)
∠C=∠F(已证)
∴△ABC≌
△
DEF
4.如图OP是∠
MON的角平分线,
C是OP上的一点,CA⊥
OM,
CB⊥ON,垂足分别为A、B,△
AOC
≌
△
BOC吗
?为什么?
O
B
N
P
M
C
┎
┛
A
解:
△
AOC
≌
△
BOC.
∵
CA
⊥
OM,
CB⊥ON.
∴
∠
CAO=
∠
CBO=90
°
.
∵
OP是∠
MON的平分线,
∴
∠
AOC=
∠
BOC
.
又∵
OC=
OC
.
∴
△
AOC
≌
△
BOC
.(ASA)
∴
∠
OCA=
∠
OCB
.
完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
