第5课时 用HL判定直角三角形全等 课件(共26张)
文档属性
| 名称 | 第5课时 用HL判定直角三角形全等 课件(共26张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 10:37:48 | ||
图片预览




文档简介
(共21张PPT)
第5课时
用HL判定直角三角形全等
沪科版·八年级数学上册
教学课件
14.2
三角形全等的判定
学习目标
【知识与技能】
学会判定直角三角形全等的特殊方法,提升合情推理能力,并熟练运用判定两个直角三角形全等的方法.
【过程与方法】
通过探索直角三角形全等条件的过程,学会运用“HL”解决实际问题;熟练掌握两个三角形全等的判定方法.
【情感与态度】
感受数学思想,激发学生的求知欲,使学生体会到逻辑推理的应用价值.
【教学重点】
重点是掌握判定直角三角形全等的特殊方法.
【教学难点】
难点是应用“HL”解决直角三角形全等的问题;三角形全等判定方法的运用.
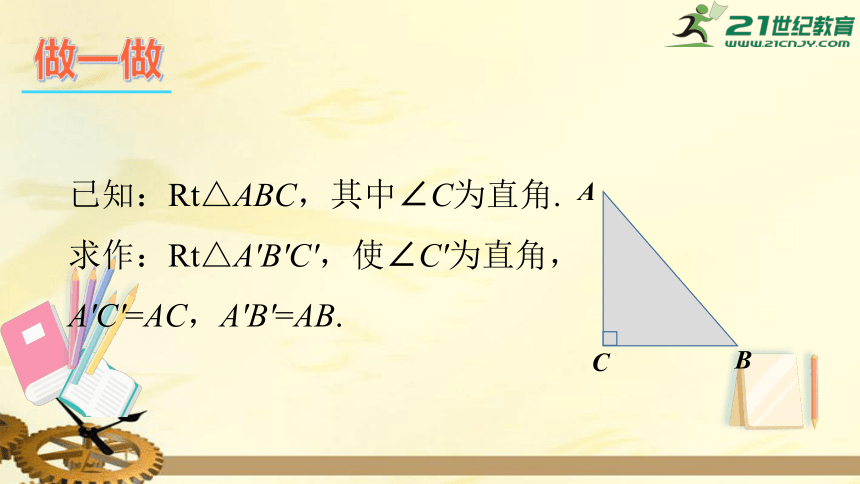
已知:Rt△ABC,其中∠C为直角.
求作:Rt△A'B'C',使∠C'为直角,A'C'=AC,A'B'=AB.
做一做
A
B
C
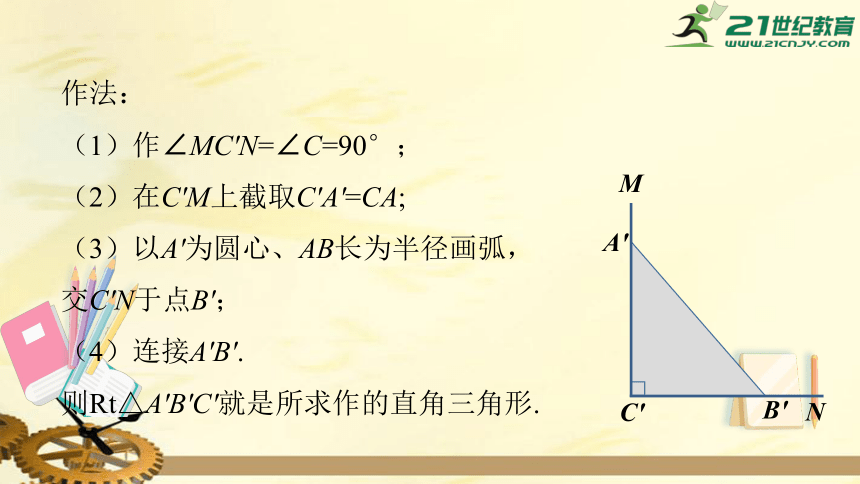
作法:
(1)作∠MC'N=∠C=90°;
(2)在C'M上截取C'A'=CA;
(3)以A'为圆心、AB长为半径画弧,交C'N于点B';
(4)连接A'B'.
则Rt△A'B'C'就是所求作的直角三角形.
A'
B'
C'
M
N
A
B
C
A'
B'
C'
M
N
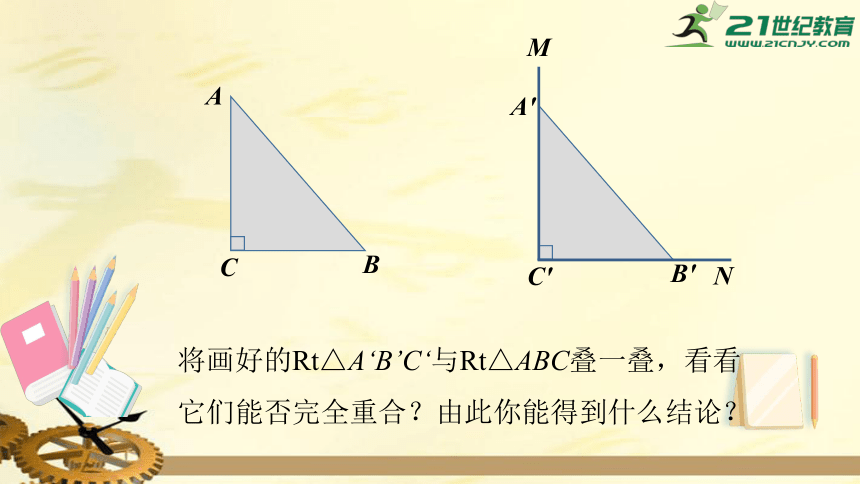
将画好的Rt△A‘B’C‘与Rt△ABC叠一叠,看看它们能否完全重合?由此你能得到什么结论?
定
理
斜边和一条直角边分别相等的两个直角三角形全等.简记为“斜边、直角边”或“HL”.
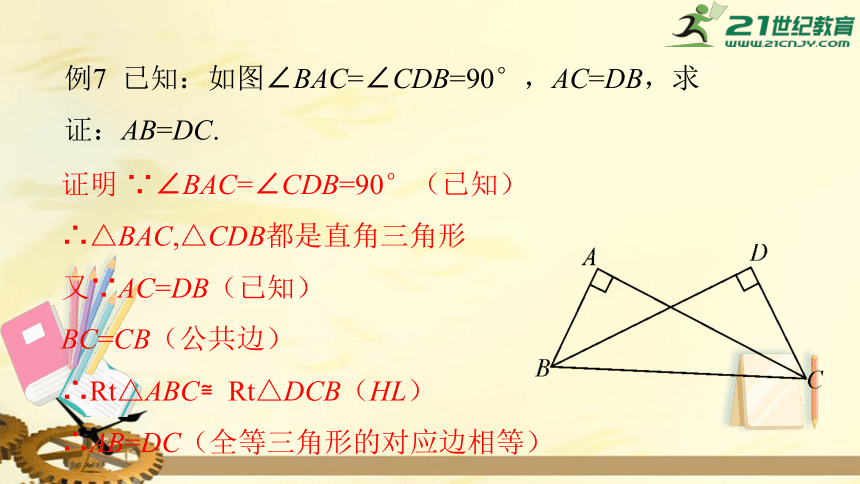
例7
已知:如图∠BAC=∠CDB=90°,AC=DB,求证:AB=DC.
证明
∵∠BAC=∠CDB=90°(已知)
∴△BAC,△CDB都是直角三角形
又∵AC=DB(已知)
BC=CB(公共边)
∴Rt△ABC≌Rt△DCB(HL)
∴AB=DC(全等三角形的对应边相等)
练
习
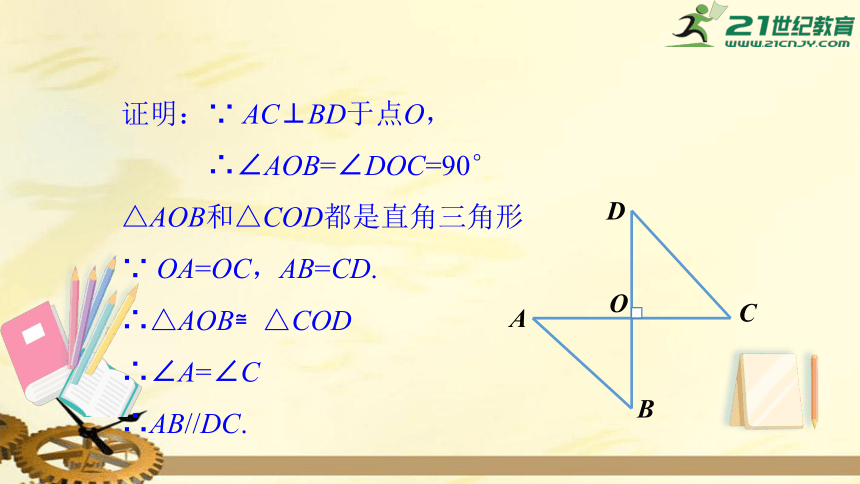
已知:如图,AC⊥BD于点O,且OA=OC,AB=CD.求证:AB//DC.
A
B
C
D
O
证明:∵
AC⊥BD于点O,
∴∠AOB=∠DOC=90°
△AOB和△COD都是直角三角形
∵
OA=OC,AB=CD.
∴△AOB≌△COD
∴∠A=∠C
∴AB//DC.
A
B
C
D
O
2.
已知:如图,P为∠AOB内一点,PD⊥OA,PE⊥OB,垂足分别为点D,E,且PD=PE,猜想∠AOP与∠BOP有什么关系?试说明理由.
O
E
B
A
P
D
∠AOP=
∠BOP
例8
已知:如图AB=CD,BC=DA,E,F是AC上的两点,且AE=CF.
求证:BF=DE.
分析
本题需要两次证明三角形全等,首先证明△ABC≌△CDA(SSS),得出∠1=∠2,再由“边角边”定理证明△DAE≌△BCF,最后证出BF=DE.
证明
在△ABC和△CDA中
AB=CD(已知)
∵
BC=DA(已知)
CA=AC(公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2(全等三角形的对应角相等)
在△BCF和△DAE中
BC=DA(已知)
∵
∠1=∠2(已证)
CF=AE(已知)
∴△BCF≌△DAE(SAS)
∴BF=DE(全等三角形的对应边相等)
例9
证明:全等三角形的对应边上的高相等.
已知:如图△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的高.
求证:AD=A′D′.
证明
∵△ABC≌△A′B′C′(已知)
∴AB=A′B′,∠B=∠B′(全等三角形的对应边、对应角相等)
∵AD、A′D′分别是△ABC和△A′B′C′的高,
∴∠ADB=∠A′D′B′=90°(垂直的定义)
在△ABD和△A′B′D′中
∠B=∠B′(已证)
∠ADB=∠A′D′B′(已证)
AB=A′B′(已证)
∴△ABD≌△A′B′D′(AAS)
∴AD=A′D′(全等三角形的对应边相等)
随堂练习
已知:如图AB=AD,AC=AE,∠BAE=∠DAC.
(1)求证:△ABC≌△ADE;
(2)BM=DN成立吗?为什么?
A
B
C
M
E
N
D
2.求证:两个全等三角形对应边上的中线相等.
3.
求证:两个全等三角形对应角的平分线相等.
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第5课时
用HL判定直角三角形全等
沪科版·八年级数学上册
教学课件
14.2
三角形全等的判定
学习目标
【知识与技能】
学会判定直角三角形全等的特殊方法,提升合情推理能力,并熟练运用判定两个直角三角形全等的方法.
【过程与方法】
通过探索直角三角形全等条件的过程,学会运用“HL”解决实际问题;熟练掌握两个三角形全等的判定方法.
【情感与态度】
感受数学思想,激发学生的求知欲,使学生体会到逻辑推理的应用价值.
【教学重点】
重点是掌握判定直角三角形全等的特殊方法.
【教学难点】
难点是应用“HL”解决直角三角形全等的问题;三角形全等判定方法的运用.
已知:Rt△ABC,其中∠C为直角.
求作:Rt△A'B'C',使∠C'为直角,A'C'=AC,A'B'=AB.
做一做
A
B
C
作法:
(1)作∠MC'N=∠C=90°;
(2)在C'M上截取C'A'=CA;
(3)以A'为圆心、AB长为半径画弧,交C'N于点B';
(4)连接A'B'.
则Rt△A'B'C'就是所求作的直角三角形.
A'
B'
C'
M
N
A
B
C
A'
B'
C'
M
N
将画好的Rt△A‘B’C‘与Rt△ABC叠一叠,看看它们能否完全重合?由此你能得到什么结论?
定
理
斜边和一条直角边分别相等的两个直角三角形全等.简记为“斜边、直角边”或“HL”.
例7
已知:如图∠BAC=∠CDB=90°,AC=DB,求证:AB=DC.
证明
∵∠BAC=∠CDB=90°(已知)
∴△BAC,△CDB都是直角三角形
又∵AC=DB(已知)
BC=CB(公共边)
∴Rt△ABC≌Rt△DCB(HL)
∴AB=DC(全等三角形的对应边相等)
练
习
已知:如图,AC⊥BD于点O,且OA=OC,AB=CD.求证:AB//DC.
A
B
C
D
O
证明:∵
AC⊥BD于点O,
∴∠AOB=∠DOC=90°
△AOB和△COD都是直角三角形
∵
OA=OC,AB=CD.
∴△AOB≌△COD
∴∠A=∠C
∴AB//DC.
A
B
C
D
O
2.
已知:如图,P为∠AOB内一点,PD⊥OA,PE⊥OB,垂足分别为点D,E,且PD=PE,猜想∠AOP与∠BOP有什么关系?试说明理由.
O
E
B
A
P
D
∠AOP=
∠BOP
例8
已知:如图AB=CD,BC=DA,E,F是AC上的两点,且AE=CF.
求证:BF=DE.
分析
本题需要两次证明三角形全等,首先证明△ABC≌△CDA(SSS),得出∠1=∠2,再由“边角边”定理证明△DAE≌△BCF,最后证出BF=DE.
证明
在△ABC和△CDA中
AB=CD(已知)
∵
BC=DA(已知)
CA=AC(公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2(全等三角形的对应角相等)
在△BCF和△DAE中
BC=DA(已知)
∵
∠1=∠2(已证)
CF=AE(已知)
∴△BCF≌△DAE(SAS)
∴BF=DE(全等三角形的对应边相等)
例9
证明:全等三角形的对应边上的高相等.
已知:如图△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的高.
求证:AD=A′D′.
证明
∵△ABC≌△A′B′C′(已知)
∴AB=A′B′,∠B=∠B′(全等三角形的对应边、对应角相等)
∵AD、A′D′分别是△ABC和△A′B′C′的高,
∴∠ADB=∠A′D′B′=90°(垂直的定义)
在△ABD和△A′B′D′中
∠B=∠B′(已证)
∠ADB=∠A′D′B′(已证)
AB=A′B′(已证)
∴△ABD≌△A′B′D′(AAS)
∴AD=A′D′(全等三角形的对应边相等)
随堂练习
已知:如图AB=AD,AC=AE,∠BAE=∠DAC.
(1)求证:△ABC≌△ADE;
(2)BM=DN成立吗?为什么?
A
B
C
M
E
N
D
2.求证:两个全等三角形对应边上的中线相等.
3.
求证:两个全等三角形对应角的平分线相等.
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
