第14章 全等三角形 本章复习 课件(共20张PPT)
文档属性
| 名称 | 第14章 全等三角形 本章复习 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 00:00:00 | ||
图片预览


文档简介
(共20张PPT)
本章复习
沪科版·八年级数学上册
教学课件
第14章
全等三角形
学习目标
【知识与技能】
学会运用三角形全等的判定方法,发展推理能力.
【过程与方法】
经历归纳、总结全等三角形的过程,深化思维能力,提高逻辑思维和表达能力.
【情感与态度】
培养合情推理的能力和创新意识.
【教学重点】
重点是判定两个三角形全等的方法.
【教学难点】
难点是运用已学过的判定三角形全等的方法,解决实际问题.
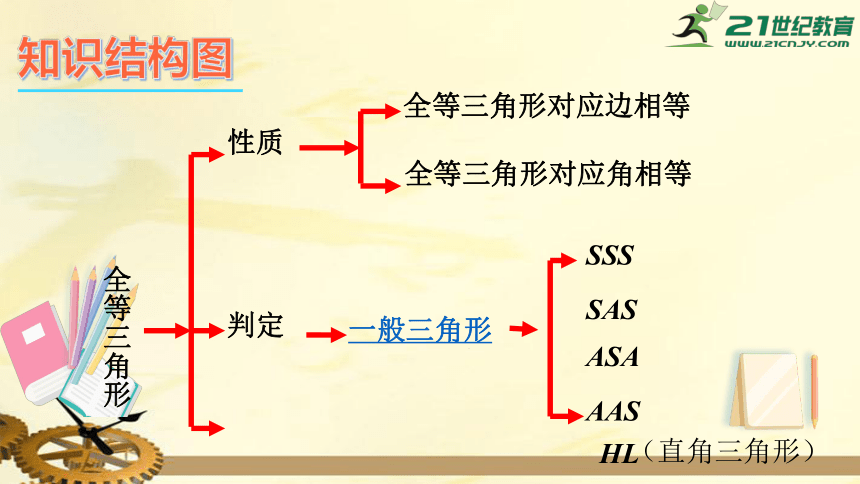
知识结构图
全等三角形
性质
判定
HL
全等三角形对应边相等
全等三角形对应角相等
SSS
SAS
ASA
AAS
一般三角形
(直角三角形)
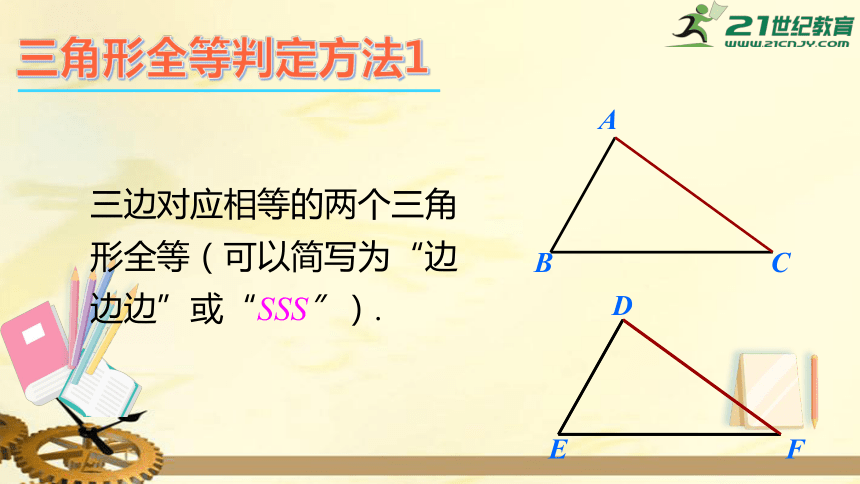
三角形全等判定方法1
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”).
A
B
C
D
E
F
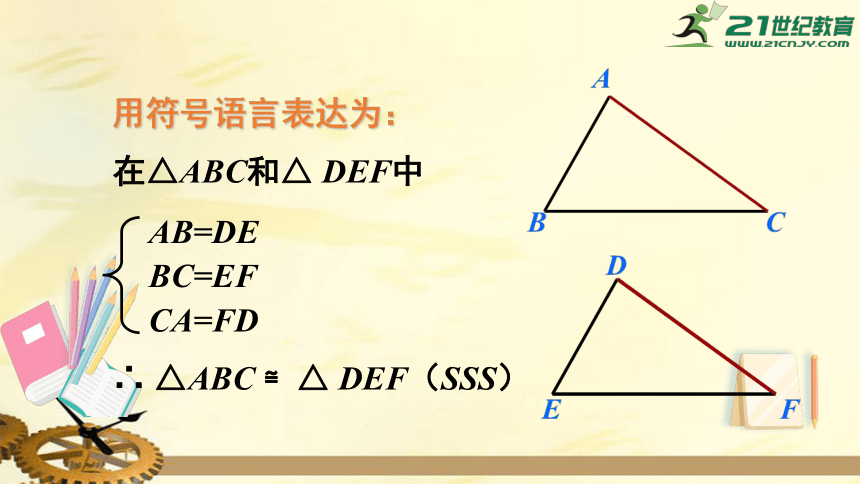
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
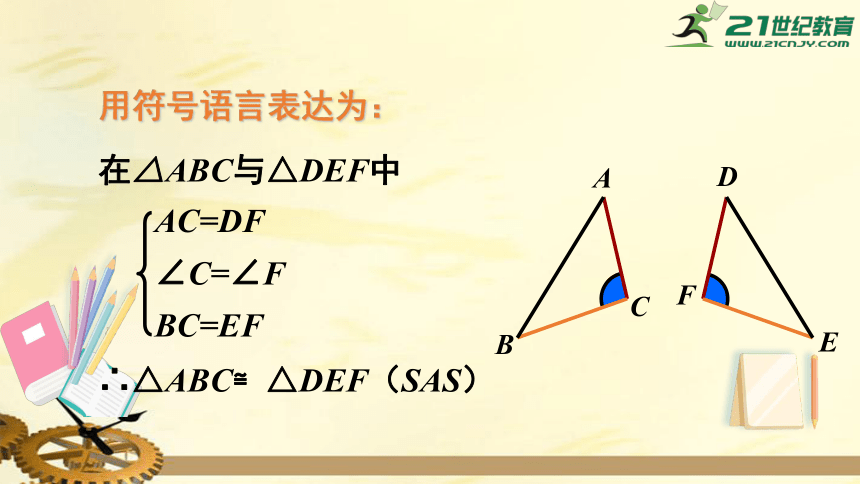
用符号语言表达为:
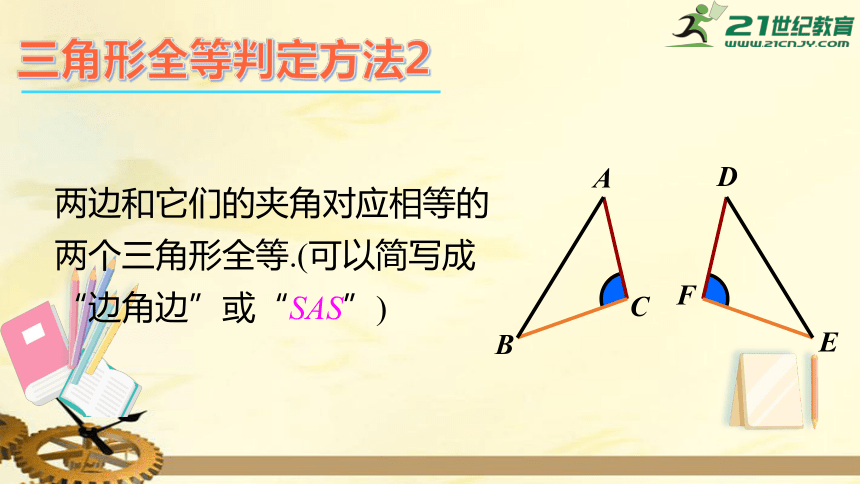
三角形全等判定方法2
两边和它们的夹角对应相等的两个三角形全等.(可以简写成“边角边”或“SAS”)
F
E
D
C
B
A
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
AC=DF
∠C=∠F
BC=EF
F
E
D
C
B
A
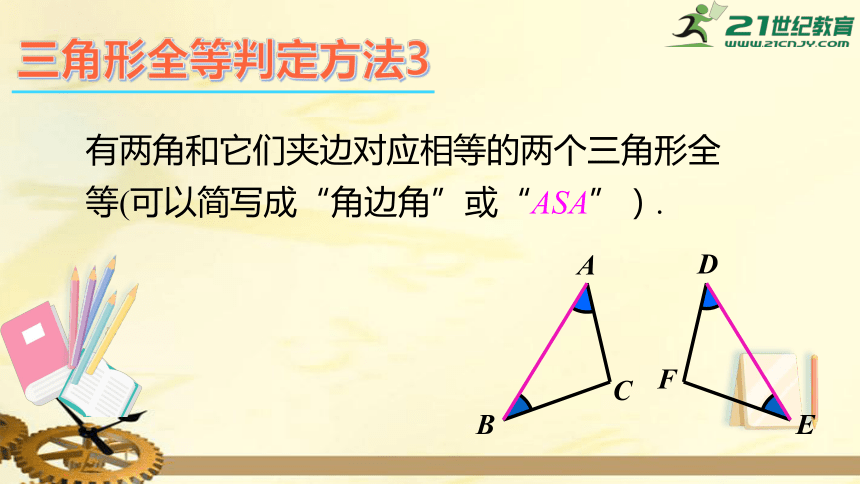
三角形全等判定方法3
有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
F
E
D
C
B
A
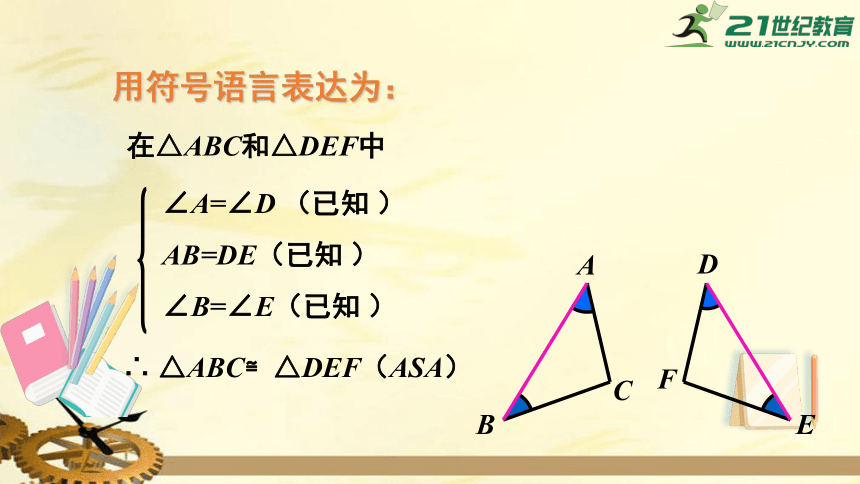
∠A=∠D
(已知
)
AB=DE(已知
)
∠B=∠E(已知
)
在△ABC和△DEF中
∴
△ABC≌△DEF(ASA)
用符号语言表达为:
F
E
D
C
B
A
三角形全等判定方法4
有两角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”).
直角三角形全等判定:HL
A
B
C
A′
B′
C′
练
习
1.
如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD.可补充的一个条件是
.
或AD=AC
或∠CBA=∠DBA
∠C=∠D
或∠CBE=∠DBE
2.
如图,AC∥
DB,AC=2DB,E是AC的中点,求证:BC=DE.
证明
∵AC=2DB,AE=EC
(已知)
∴DB=EC
又∵
AC∥
DB(已知)
∠DBE=∠CEB
(两直线平行,内错角相等)
∵BE=EB(公共边)
∴
ΔDBE≌ΔCEB(SAS)
∴
BC=DE
(全等三角形的对应边相等)
3.
如图,在ΔABC和ΔDEF中,A、E、B、D在同一直线上,
AB=DE,AC=DF,AC
∥
DF.
(1)求证:
ΔABC≌ΔDEF;
(2)你还可以得到的结论是
.
(写出一个,不再添加其他线段,不再标注或使用其他字母)
(1)证明
∵AC∥DF(已知)
∴∠A=∠D
(两直线平行,内错角相等)
在ΔABC和ΔDEF中
AB=DE(已知)
∠A=∠D(已证)
AC=DF
(已知)
∴ΔABC≌ΔDEF(SAS)
(2)解:根据”全等三角形的对应边(角)相等”可知:
①BC=EF,
②∠C=∠F,
③∠ABC=∠
DEF,
④
EF∥BC,
⑤AE=DB等.
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
本章复习
沪科版·八年级数学上册
教学课件
第14章
全等三角形
学习目标
【知识与技能】
学会运用三角形全等的判定方法,发展推理能力.
【过程与方法】
经历归纳、总结全等三角形的过程,深化思维能力,提高逻辑思维和表达能力.
【情感与态度】
培养合情推理的能力和创新意识.
【教学重点】
重点是判定两个三角形全等的方法.
【教学难点】
难点是运用已学过的判定三角形全等的方法,解决实际问题.
知识结构图
全等三角形
性质
判定
HL
全等三角形对应边相等
全等三角形对应角相等
SSS
SAS
ASA
AAS
一般三角形
(直角三角形)
三角形全等判定方法1
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”).
A
B
C
D
E
F
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法2
两边和它们的夹角对应相等的两个三角形全等.(可以简写成“边角边”或“SAS”)
F
E
D
C
B
A
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
AC=DF
∠C=∠F
BC=EF
F
E
D
C
B
A
三角形全等判定方法3
有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
F
E
D
C
B
A
∠A=∠D
(已知
)
AB=DE(已知
)
∠B=∠E(已知
)
在△ABC和△DEF中
∴
△ABC≌△DEF(ASA)
用符号语言表达为:
F
E
D
C
B
A
三角形全等判定方法4
有两角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”).
直角三角形全等判定:HL
A
B
C
A′
B′
C′
练
习
1.
如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD.可补充的一个条件是
.
或AD=AC
或∠CBA=∠DBA
∠C=∠D
或∠CBE=∠DBE
2.
如图,AC∥
DB,AC=2DB,E是AC的中点,求证:BC=DE.
证明
∵AC=2DB,AE=EC
(已知)
∴DB=EC
又∵
AC∥
DB(已知)
∠DBE=∠CEB
(两直线平行,内错角相等)
∵BE=EB(公共边)
∴
ΔDBE≌ΔCEB(SAS)
∴
BC=DE
(全等三角形的对应边相等)
3.
如图,在ΔABC和ΔDEF中,A、E、B、D在同一直线上,
AB=DE,AC=DF,AC
∥
DF.
(1)求证:
ΔABC≌ΔDEF;
(2)你还可以得到的结论是
.
(写出一个,不再添加其他线段,不再标注或使用其他字母)
(1)证明
∵AC∥DF(已知)
∴∠A=∠D
(两直线平行,内错角相等)
在ΔABC和ΔDEF中
AB=DE(已知)
∠A=∠D(已证)
AC=DF
(已知)
∴ΔABC≌ΔDEF(SAS)
(2)解:根据”全等三角形的对应边(角)相等”可知:
①BC=EF,
②∠C=∠F,
③∠ABC=∠
DEF,
④
EF∥BC,
⑤AE=DB等.
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
